2. 3. 2. Охлаждение (нагрев) одномерных тел

      2. 3. 2. ОХЛАЖДЕНИЕ (НАГРЕВ) ОДНОМЕРНЫХ ТЕЛ

   Для одномерных тел (неограниченной пластины и бесконечно длинного цилиндра) дифференциальное уравнение теплопроводности (2. 53) с учетом (2. 57) приводится к виду:

для пластины

                                        ∂ θ / ∂ t = α ∂ ²θ / ∂ x²;                              (2. 65)

для цилиндра

                            ∂ θ / ∂ t = α ( ∂ ²Т / ∂ r² + (1/r)(∂ Т / ∂ r).              (2. 66)                                 

       

При Fo ≥ 0, 3 уравнение (2. 62), описывающее изменение во времени безразмерной температуры θ _ц/θ _о на средней плоскости пластины (стенки) x = 0, оси цилиндра r = 0, примет вид:

 

                              θ _ц/θ _о = N(Bi)exp(-μ ₁²Fo),                                (2. 67)

 

а  на поверхностях этих тел:

 

                                 θ _ст/θ _о = P(Bi)exp(-μ ₁²Fo),                              (2. 68)

 

где N(Bi) и P(Bi) – функции, зависящие от Bi;

                   μ ₁  - первый корень характеристического трансцендент-

                          ного уравнения μ =μ (Bi).

Применение уравнений (2. 67) и (2. 68) на практике связано с необходимостью выполнения трудоемких расчетов. Поэтому для тел простой формы (пластины, цилиндра ), размеры которых представлены на рис. 2. 10, с помощью этих уравнений построены графики, использование которых сводит расчеты к весьма простым операциям.

На рис. 2. 11 – 2. 14 представлены графики функций θ _ц/θ _о = f ( Fo, Bi)

и θ _ст. /θ _о = f ( Fo, Bi) для  ξ /l  = 0 и  ξ /l  = 1, которые соответственно характеризуют температуру плоскости (оси) симметрии и поверхностей стенки и цилиндра. Прежде, чем воспользоваться графиками для

                              

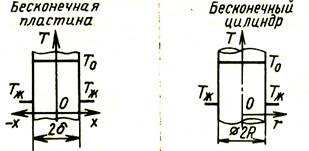
                                Рис. 2. 10. Форма и размер тела

 

определения температуры тела, необходимо вычислить значения чисел Био и Фурье. Аналогичные графики имеются и для шаров.

 

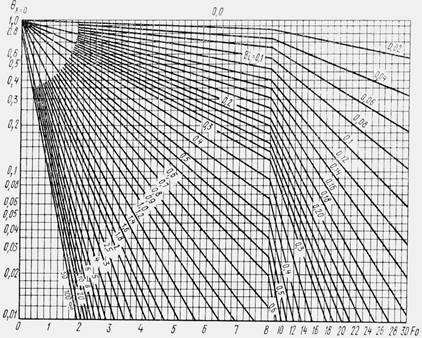
Рис. 2. 11. Безразмерная температура в середине бесконечной пластины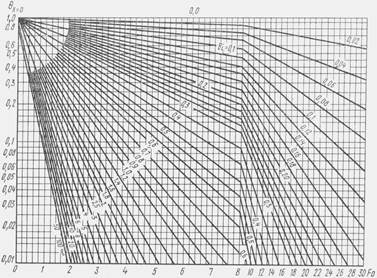

 Рис. 2. 12. Безразмерная температура на поверхности бесконечной

                                                   пластины                                                  

Рис. 2. 13. Безразмерная температура на оси цилиндра бесконечной                                     

                                               длины

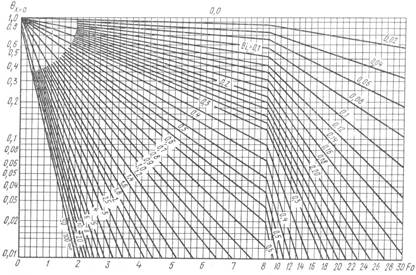
  Рис. 2. 14. Безразмерная температура на поверхности цилиндра

                                       бесконечной длины

 

Из рис. 2. 12 и 2. 14 видно, что при Bi ≥ 100 температура стенки перестает зависеть от условий теплообмена на границах тела. Это объясняется тем, что при этом тепловое сопротивление внешнего теплообмена становится неизмеримо малым по сравнению с внутренним сопротивлением, и потому температурное поле определяется условиями распространения теплоты внутри тела.

Для решения некоторых задач об охлаждении или нагревании тел сложной конфигурации разработаны приближенные методы решения, из которых чаще всего применяют метод конечных разностей.

Количество полученной или отданной стенкой теплоты также определяется числами Fo и Bi. Обозначим через Q_o количество потерянной (или полученной) теплоты при t → ∞ (когда температуры тела и среды выравниваются), а через Q_t  теплоту, отданную (или полученную) по истечении времени  t. Тогда для стенки с плотностью материала ρ и теплоемкостью с можно записать:

 

                                Q_o  = 2δ ρ с(Т_о – Т_ж) = 2δ ρ сθ _о,                         (2. 69)

                              

                             Q_t  =  2δ ρ с(Т_о – Т_ср) = 2δ ρ с(θ _{о –} θ _ср),                  (2. 70)

 

где  Т_ср – средняя температура стенки по истечении периода времени t.

Поделив почленно второе равенство на первое, получим:

 

                                        Q_t  / Q_o  = 1 -  θ _ср/θ _о.                                 (2. 71)

 

В каждый момент времени температурное поле стенки определяется числами Fo и Bi. Поэтому и средняя температура стенки Т_ср будет зависеть только от этих чисел. Следовательно,  

                                               

                              Q_t  / Q_o  = f ( Fo, Bi).                             (2. 72)

     

График этой функции имеется в справочной литературе.

 

 

  2. 3. 3. РЕГУЛЯРНЫЙ РЕЖИМ ОХЛАЖДЕНИЯ (НАГРЕВА)

     Анализ решений дифференциального уравнения теплопроводности

                                

                                           ∂ Т/ ∂ t = α Ñ ² Т                         (2. 73)

 

показывает, что безразмерную избыточную температуру θ /θ _о можно выразить суммой произведений из трех величин:

 

                                                  _n=∞

                                       θ /θ _о = ∑ A_nU_nexp(-m_nt),                          ( 2. 74)

                                          ⁿ⁼¹

 где А_n - постоянные, зависящие от формы тела и начального

          распределения температур;

  U_n - функции координат, характеризующие изменение температуры в пространстве;

  m_n – постоянные, представляющие собой ряд положительных возрастающих чисел

                                       m₁ < m₂ < m₃ < ... < m_n.                              (2. 75)

 

Такая форма записи безразмерной температуры пригодна не только для простейших тел правильной формы, но и для любых других тел, форма которых отражается на виде множителей А_n и U_n .

При небольшой продолжительности процесса теплообмена от t = 0  до t = t_р  температурное поле определяется не только первым, но и последующими членами ряда. Температура в некоторых точках тела и скорость ее изменения зависят от начального распределения температур в теле. Это так называемая неупорядоченная стадия процесса охлаждения или нагревания.

     Благодаря неравенству (2. 75) с увеличением времени t ряд быстро сходится и все члены его, кроме первого, стремятся к нулю. При t, превышающем некоторое определенное значение t > t_р, начальные условия начинают играть второстепенную роль, и процесс полностью определяется только условиями охлаждения (нагревания) на поверхности тела, его физическими свойствами, геометрической формой и размерами. Вторая стадия охлаждения (нагревания) называется регулярным режимом и описывается первым членом ряда (индексы опущены):

 

                                        θ /θ _о = АUexp(-mt),                                 (2. 76)

 

 где m = μ ₁²α /l²  - темп регулярного режима.

     Логарифмируя уравнение (2. 76), получим:

 

                                           ln θ = - mt + С,                                  (2. 77)

 

где С = ln θ _оАU – функция от координат.

     Из полученного уравнения видно, что регулярный режим теплопроводности характеризуется тем, что натуральный логарифм избыточной температуры θ = Т–Т_ж любой точки тела изменяется во времени по линейному закону, а начальное распределение температур в теле не оказывает влияния на форму этого уравнения. Это позволяет легко обнаружить в эксперименте наступление регулярного режима и, фиксируя температуру в произвольной точке тела для двух моментов времени t₁ и t₂, рассчитать темп охлаждения:

 

                                     m = (ln θ ₁ - ln θ ₂) / (t₂ – t₁).                    (2. 78)

 

 На рис. 2. 15 показано изменение температуры в двух точках тела при его охлаждении.

 

 

                                   

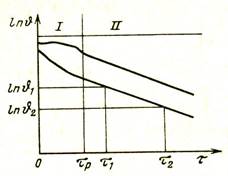
               Рис. 2. 15. Изменение во времени температуры тела

               при его охлаждении: I – неупорядоченный процесс;

                                       II – регулярный режим

 

Дифференцируя уравнение (2. 77) по времени, получим

 

                                    m = - (1/θ )(∂ θ /∂ t).                                    (2. 79)

 

      Из этого уравнения следует, что темп регулярного режима охлаждения (нагревания) тела не зависит ни от координат, ни от времени и представляет собой относительную скорость изменения температуры. Он выражается в 1/с и в любой точке тела остается постоянным.

Темп регулярного режима определяется геометрической формой и размерами тела, его физическими свойствами и условиями теплообмена на поверхности тела (зависит от коэффициента теплоотдачи α ).

     Теория регулярного режима была разработана Г. М. Кондратьевым и применена им для определения теплофизических свойств тел (α , λ, с), коэффициента теплоотдачи α на поверхности тела, омываемого потоком жидкости, коэффициентов излучения.

Третья стадия охлаждения (нагревания) называется стационарным режимом - при   t → ∞ температура во всех точках тела становится равной температуре окружающей жидкости.

 

                           

 

                    Контрольные вопросы

 

1. Приведите примеры нестационарной теплопроводности.
2. Опишите характер изменения температуры тела при его нагревании и охлаждении.
3. От каких параметров зависит температура любой точки тела при нестационарной теплопроводности.
4. Уравнение для безразмерной избыточной температуры тела.
5. Что представляют собой числа Био и Фурье?
6. Уравнение, описывающее нестационарное температурное поле в твердом теле.
7. Уравнения, описывающие изменение во времени безразмерной температуры для пластины и цилиндра.
8. Как пользоваться графиками для определения температуры тела при нестационарной теплопроводности.
9. Что называется регулярным режимом нагревания (охлаждения) тела.
10. По какой формуле рассчитывается темп охлаждения тела.

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: