4. Теплообмен излучением.   4. 1. Общие положения.   4. 1. 1. Основные понятия и определения. Полный поток излучения

  4. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ

 

                              

                     4. 1. ОБЩИЕ ПОЛОЖЕНИЯ

 

    4. 1. 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

      Лучистый (радиационный) теплообмен осуществляется в результате процессов превращения внутренней энергии вещества в энергию излучения, переноса энергии излучения в пространстве и ее поглощения другим веществом с последующим преобразованием этой энергии во внутреннюю или ее рассеянием.. Существенное отличие лучистого теплообмена от других видов теплообмена (теплопроводности, конвективного теплообмена) заключается в том, что такой теплообмен не требует непосредственного контакта тел. Он может протекать и при отсутствии материальной среды, разделяющей поверхности тепло-обмена, так как осуществляется в результате распространения энергии от излучающего тела в форме квантов энергии электромагнитных волн.

Электромагнитные волны различаются между собой длиной волны. В зависимости от длины волны λ лучи обладают различными свойствами. Наименьшей длиной волны обладают космические лучи λ = 0, 1 – 10 ^оА (1^оА = 10^-10м). Гамма-лучи, испускаемые радиоактивными веществами, имеют длину волны до 10^оА; лучи Рентгена – λ = 10 – 200^оА; ультрафиолетовые лучи - λ = 0, 02 – 0, 4мкм (мкм – микрометр, 1 мкм = 0, 001мм); световые лучи - λ = 0, 4 – 0, 8 мкм; инфракрасные или тепловые лучи - λ = 0, 8 – 400 мкм; радио лучи - λ > 400 мкм.

Для теплообмена излучением наибольший интерес представляют ультрафиолетовое, видимое или световое и инфракрасное или тепловое излучения. При любой температуре, кроме Т = 0 К, все тела испускают электромагнитные волны разных длин. Однако той или иной температуре соответствует преимущественный вид излучения. Например, твердое тело при 1800 К излучает 0, 003% энергии в ультрафиолетовой части спектра, 1, 6% - в видимой, а остальные 98, 397% - в инфракрасной. Повышение температуры в этом случае при-ведет к увеличению доли тепловой энергии, переносимой излучением в видимой и ультрафиолетовой частях спектра.

Скорость с кванта энергии, длина электромагнитной волны λ и частота колебаний ν электромагнитного поля связаны соотношением:

 

                                                с = λ ν.                                                (4. 1)

 

В вакууме с = с_о = 2, 9977·10⁸ м/с (скорость света в пустоте). В других средах с < с_о. В газах обычно оправдано приближение с ≈ с_о. В ряде жидкостей и твердых тел скорость света падает примерно до с = 0, 7с_о. Когда излучение переходит из одной среды в другую, а скорости света в этих средах разные, то согласно уравнению (4. 1) изменяется длина волны λ, тогда как частота ν остается неизменной. Энергия кванта равна

hν и при таком переходе не меняется. Здесь h = 6, 63·10^-34 Дж ·с – посто-янная Планка.

  В инженерной практике интерес представляют осредненные характеристики процесса излучения тела:

 интегральная плотность потока полусферического излучения Е, Вт/м², - поток энергии, переносимой квантами разных частот, пересекающими единичную площадку во всех направлениях про-странства полусферы;

полный поток излучения

                                                    Q = ∫ ЕdF, Вт,                               (4. 2)

                                                           ^F

передаваемого через поверхность конечной площади F. При постоянной плотности интегрального излучения Е излучающей поверхности пол-ный лучистый поток Q определяется соотношением:

 

                                                             Q = ЕF.                                               (4. 3)

 

Распределение энергии излучения по частотам или длинам волн характеризуется спектром излучения.

Спектральная или, что то же самое, монохроматическая плот-ность потока полусферического излучения относится либо к единич-ному интервалу частот

                                                Е_ν = dЕ/dν,                                         (4. 4)

 

либо к единичному интервалу длин волн

 

                                                Е_λ = dЕ/dλ.                                         (4. 5)

 

В первом случае размерность спектральной плотности Вт·с/м², во втором – Вт/(м²·м).

  Значения Е_ν и Е_λ связаны между собой соотношением:

                                                  ν Е_ν = λ Е_λ .                                       (4. 6)

 

В общем случае тело, на которое падает лучистый поток, частично поглощает его, частично отражает и частично пропускает (рис. 4. 1).

На основании закона сохранения энергии можно записать:

                                     Q_пад = Q_А + Q_R + Q_D                                        (4. 7)

 

В безразмерном виде

                                          А + R + D =1,                                        (4. 8)

 

где А = Q_А /Q_пад – коэффициент поглощения;

R = Q_R /Q_пад – коэффициент отражения;

D = Q_D /Q_пад – коэффициент пропускания.

 

                 

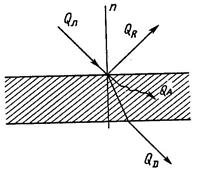
                    Рис. 4. 1. Распределение лучистого теплового

                                   потока, падающего на тело

    

Такое же соотношение имее место и для монохроматического излучения (т. е. для излучения с определенной длиной волны):

 

                                         А_λ  + R_λ + D_λ = 1.                                     (4. 9)

 

Для одного и того же тела при различных длинах волн величины А_λ ,  R_λ и D_λ могут иметь существенно различные значения. Так, обычное стекло хорошо пропускает световые лучи, но почти не пропускает ультрафиолетовые и инфракрасные лучи.

Коэффициенты поглощения, отражения и пропускания зависят от природы тел и состояния их поверхности. Как видно пз формулы (4. 8), их значения могут изменяться в пределах от 0 до 1.

Тело, которое полностью поглощает всю падающую на него лучистую энергию, называется абсолютно черным. Для такого тела А= = 1 и R = D =0. В дальнейшем все величины, относящиеся к абсолютно черному телу, будут обозначаться индексом «0», например А_о =1.

Тело, отражающее всю падающую на него лучистую энергию, называется абсолютно белым. В этом случае R = 1 и A = D = 0. Если отражение имеет правильный характер (угол падения равен углу отражения), то такие тела называются зеркальными.

Тела, пропускающие всю падающую на них лучистую энергию, называются абсолоютно прозрачными (диатермичными). Для них D= = 1 и A = R = 0.

В природе абсолютно черных, белых и прозрачных тел не существует. Наиболее близки к абсолютно черному телу сажа и бархат (А = 0, 97 – 0, 98), к абсолютно белому телу – полированные металлы (R= = 0, 97). Сухой воздух, одно- и двухатомные газы (при температуре ниже 2500 – 3000 К) можно с хорошим приближением рассматривать как диатермичные (абсолютно прозрачные) среды (D ≈ 1).

Большинство конструкционных твердых тел (металлы, сплавы, теплоизоляционные материалы) и ряд жидкостей (спирты, вода) для тепловых лучей при заметных толщинах слоя веществ практически непрозрачны (D ≈ 0). При этом

                                              А + R = 1.                                        (4. 10)

 

Для металлов D → 0 уже при толщине приблизительно 1 мкм, для диэлектриков – при толщинах около 1 мм. Поэтому для упрощения рассмотрения часто полагают, что процессы поглощения и отражения, определяемые соотношением (4. 10) протекают на самой поверхности этих тел. Если на поверхность такого тела извне не падает лучистая энергия, то единственный поток энергии, который можно зарегистрировать, будет исходить с поверхности тела и передаваться в окружающее пространство. Этот поток энергии с плотностью Е₁ называется собственным излучением тела. При сделанных выше оговорках можно считать, что это излучение формируется на самой поверхности тела и, следовательно, зависит лишь от температуры, материала и состояния поверхности. В реальных условиях  со стороны внешнего окружения на поверхность тела падает какой-то внешний поток лучистой энергии - падающее излучение плотностью  Е_пад. Часть этого потока в количестве  А₁Е_пад поглощается телом - поглощенное излучение. Часть в количестве

 

                                     R₁Е_пад = (1 – А₁)Е_пад                                  (4. 11)

 

отражается поверхностью тела – отраженное излучение. Сумма соб-ственного и отраженного излучения образует эффективное излучение данного тела:

                                        Е_эф1 = Е₁ + (1 – А₁)Е_пад,                          (4. 12)

 

которое и регистрирует прибор. Наконец, разность между собственным и поглощенным излучением образует результирующее излучение:

 

                                            Е_рез1 = Е₁ – А₁Е_пад.                               (4. 13)

 

Величина Е_рез1 показывает суммарный расход (приход) энергии вследствие лучистого теплообмена с окружающей средой. Во многих случаях на практике – это искомая величина в инженерных тепловых расчетах.

 

 

  

                4. 1. 2. ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ

      Наиболее простыми и строгими законами описывается излучение абсолютно черного тела. Эти законы с соответствующими поправками используются для получения расчетных формул теплообмена излучением между реальными телами.

Закон Планка. Этот закон устанавливает зависимость плотности потока монохроматического излучения абсолютно черного тела от длины волны λ и температуры Т, т. е устанавливает характер спектра излучения абсолютно черного тела. Распределение энергии по длинам волн, даваемое законом Планка, имеет вид:

 

                          Е_оλ = dE_о/dλ = С₁λ ^-5/[exp(C₂/λ T) – 1],                 (4. 14)

 

где Е_оλ – спектральная плотность излучения абсолютно черного тела                         

            Вт/(м²·м);

   С₁ – константа, С₁ = 2π hc_o² = 3, 74·10^-16 Вт·м²;

   С₂ – константа, С₂ = hc_o/k = 1, 44·10^-2 м·К;

h = 6, 63·10^-34 Дж·с – постоянная Планка;

k = 1, 38·10^-23 Дж/К – постоянная Больцмана;

с_о = 3·10⁸ м/с – скорость света в вакууме.

Графическое изображение зависимости (4. 14) показано на рис. 4. 2.

     Из рис. 4. 2 видно, что для любой температуры плотность потока (интенсивность) монохроматического излучения Е_оλ возрастает от нуля (при λ = 0) до своего наибольшего значения, а затем убывает до нуля (при λ = ∞ ). При повышении температуры интенсивность излучения для каждой длины волны возрастает. Кроме того, из рис. 4. 2 следует, что при обычно встречающихся на практике температурах основной вклад в излучение дает диапазон длин волн примерно от 0, 4мкм до нескольких сотен микрометров, который именуется «тепловым»

                                       

 

                        Рис. 4. 2. Зависимость спектральной плотности

                             потока излучения абсолютно черного тела

                                       от длины волны и температуры

 

Закон Вина. На рис. 4. 2 четко просматривается смещение максимума излучения в сторону коротких волн. Эта закономерность была замечена Вином еще до открытия закона Планка, поэтому закон и носит его имя. Математическое выражение закона Вина устанавливается из того факта, что каждой температуре Т соответствует длина волны λ _max, для которой значение Е_оλ максимально. Условие экстремума   dЕ_оλ /dλ = 0 приводит к соотношению:

 

                                            λ _maxТ = 2, 9·10^-3 м·К,                           (4. 15)

 

Следовательно, с увеличением температуры максимум плотности потока монохроматического излучения сдвигается в сторону более коротких длин волн. При температуре Солнца около 6000 К λ _max= =0, 48мкм, т. е. световые лучи обладают наибольшей плотностью потока монохроматического излучения.

Наглядным качественным подтверждением закона Вина является тот факт, что раскаленный металл по мере повышения температуры принимает сначала красный, затем оранжевый и желтый цвета, соответствующие более коротким длинам волн в области видимого спектра.

  Закон Вина широко используется в науке и технике. Так, зная длину волны, соответствующую максимуму спектральной плотности потока полусферического излучения, можно определить температуру излучателя.

Закон Стефана-Больцмана. Законы Планка и Вина хорошо вскрывают особенности теплового излучения, но для инженерных расчетов их трудно использовать. Поэтому в анализе теплообмена излучением широко применяют интегральную плотность потока полусферического излучения Е_о абсолютно черного тела_. Она определяется интегрированием энергии по спектру закона Планка:

                                                   ∞                            

                                           Е_о = ∫ Е_оλ dλ = σ Т⁴,                               (4. 16)

                                                   ⁰

 где σ = 5, 67·10^-8 Вт/(м² · К⁴) – постоянная Стефана-Больцмана.

Равенство (4. 16), показывающее, что интегральная плотность потока излучения Е_о, Вт/м², пропорциональна четвертой степени температуры абсолютно черного тела, названо законом Стефана-Больцмана. Исторически этот закон был установлен И. Стефаном экспериментально в 1879 г. и Л. Больцманом теоретически в 1884 г. еще до открытия закона Планка.

Для практических расчетов этот закон записывают в виде:

 

                                           Е_о = С_о(Т/100)⁴,                                   (4. 17)

 

где С_о=5, 67 Вт/(м²·К⁴) – коэффициент излучения абсолютно черного тела.

В таблице 4. 1 приведены характеристики энергии излучения абсолютно черного тела.

 

Табл. 4. 1. Характеристики энергии излучения абсолютно черного тела

Т, К

 

Ео, МВт/м2

0, 083

0, 372

0, 907

14, 515

35, 44

 

%-ное распределение энергии в частях спектра:

 

ультрафиолетовой

-

-

0, 1

1, 1

19, 6

 

видимой

0, 06

5, 40

9, 70

66, 60

67, 70

 

инфракрасной

99, 4

94, 60

90, 20

32, 30

12, 70

 

λ max, мкм

2, 72

1, 87

1, 50

0, 75

0, 60

 

Анализ данных табл. 4. 1 показывает, что интегральная плотность потока излучения существенно возрастает с ростом температуры, при этом меняется и распределение энергии в спектре излучения. При 5000 К

(дуговой электрический разряд) доли энергии, излучаемой в ультрафиолетовой и инфракрасной частях спектра, становятся сопоставимыми.

Реальные тела по своим радиационным свойствам отличаются от абсолютно черных тел прежде всего тем, что поглощают и излучают при равных температурах, площадях и ориентации в пространстве меньше тепловой энергии. Собственное излучение реальных тел Е(Т) можно представить как долю излучения абсолютно черного тела при той же температуре:

                                              ε (Т) = Е(Т)/Е_о(Т),                              (4. 18)

 

где ε (Т) – интегральный коэффициент теплового излучения тела (степень черноты реального тела), зависящий от материала, состояния поверхности и температуры тела (ε < 1).

Для многих технических поверхностей зависимость ε от температуры достаточно слабая, так что соотношение (4. 18) дает удобную формулу для расчета излучения реальных тел:

 

                                             Е = ε С_о(Т/100)⁴.                                  (4. 19)

 

В этой формулировке закон Стефана-Больцмана широко используется на практике для анализа высокотемпературных тепловых явлений, в которых роль теплового излучения значительна.

Для некоторых технически важных материалов примерные значения ε приведены в табл. 4. 2. В ответственных случаях рекомендуется определять ε  экспериментально.

Закон четвертой степени подтверждается для реальных тел только приближенно. Наибольшие отклонения от этого закона наблюдаются у металлов и газов. У металлов эта степень больше, а у газов – меньше четырех. Однако для расчетной оценки потоков излучения используется закон четвертой степени, т. е. формула (4. 19), а несоответствие этой формулы действительной зависимости поверхностной плотности потока собственного излучения от температуры учитывается выбором степени черноты тела.

Закон Кирхгофа. Закон устанавливает связь между излучательной и поглощательной способностью тел, находящихся в тепловом равновесии (количество излученной и поглощенной телом энергии одинаково):

 

                                                   Е/А = Е_о.                                 (4. 20)

 

Уравнение (4. 20) составляет содержание закона Кирхгофа: отношение поверхностной плотности Е потока собственного излучения тела к его поглощательной способности А, одинаково для всех тел, находящихся при одной и той же температуре, и равно поверхностной плотности Е_о потока собственного излучения абсолютно черного тела при той же температуре.

Из уравнения (4. 20) следует, что чем больше тело поглощает, тем больше оно излучает, поэтому для конкретной температуры абсолютно черное тело имеет наибольшую поверхностную плотность потока собственного излучения.

Диатермичные (абсолютно прозрачные) тела не поглощают энергию излучения, следовательно, в соответствии с законом Кирхгофа они не могут излучать.

 

Таблица 4. 2. Значения степени черноты для различных материалов

Материал

t, оС

ε

 

Алюминий полированный

225 - 575

0, 039 - 0, 057

 

Алюминий окисленный при 600 оС

200 - 600

0, 11 - 0, 19

 

Сталь листовая шлифованная

940 - 1100

0, 55 - 0, 61

 

Сталь окисленная при 600 оС

200 - 600

0, 80

 

Чугун окисленный при 600 оС

200 - 600

0, 64 - 0, 78

 

Железо окисленное гладкое

125 - 525

0, 78 - 0, 82

 

Цинк окисленный при 400 оС

0, 11

 

Оцинкованное листовое железо блестящее

0, 228

 

Асбестовая бумага

40 - 370

0, 93 - 0, 945

 

Вода

0 - 100

0, 95 - 0, 963

 

Кирпич красный

0, 93

 

Кирпич огнеупорный

-

0, 8- 0, 9

 

Масляные краски различных цветов

0, 92 - 0, 96

 

Стекло гладкое

0, 937

 

Сажа, свечная копоть

95 - 270

0, 952

 

Толь

0, 91

 

Штукатурка шероховатая известковая

10 - 88

0, 91

   

Если в уравнении (4. 20) величину Е выразить через степень черноты

Е = ε Е_о, то это уравнение примет вид:

                              

                                             ε /А = 1.                                              (4. 21)

 

Следовательно, А = ε, т. е. коэффициент поглощения численно равен степени черноты данного тела.

Если тело отдает или получает теплоту излучением, то теплового равновесия нет. В этих условиях поглощательная способность зависит как от температуры самого тела, так и от температуры источника излучения. Э. Эккерт нашел, что в этом случае для металлов равенство А = ε будет справедливым, если степень черноты тела определять по среднегеометрической температуре √ Т₁Т₂.

Закон Ламберта. Закон Ламберта дает возможность определить зависимость изменения энергии лучистого потока от его направления по отношению к поверхности тела.

Рассмотрим излучение с элементарной площадки dF на поверхности тела (рис. 4. 3). Общее количество энергии, излучаемой по всем направлениям в пределах полусферы с 1 м² поверхности в единицу времени, равно лучеиспускательной способности (интегральной плотно-сти потока излучения) Е = ε С_о(Т/100)⁴.

 

 

Рис. 4. 3. Излучение с элементарной площадки на поверхности тела

 

Если же рассматривать излучение тела лишь в направлении нормали Е_n, то интегральная плотность потока излучения в этом случае в π = 3, 14 раз меньше аналогичной характеристики полусферического излучения:

 

                                                 Е_n = Е/π.                                          (4. 22)

 

Для любого другого направления энергия лучистого потока меньше, чем по нормали к поверхности, и выражается формулой

 

                                               Е_φ = Е_n cos φ,                                     (4. 23)

 

где φ – угол между направлением излучения и нормалью (см. рис. 4. 3).

 Окончательно получим

                            

                     Е_φ = Е_n cos φ = Еπ ^-1cos φ = ε π ^-1С_о(Т/100)⁴ cos φ.      (4. 24)

 

Закон Ламберта справедлив для абсолютно черных тел. Для ре-альных тел при φ > 60^о действительные потоки энергии излучения от шероховатых поверхностей меньше, а от полированных металлических поверхностей больше, чем рассчитанные по (4. 24).

 

                            Контрольные вопросы

1. Как осуществляется теплообмен излучением?
2. Какие лучи дают наибольший вклад в теплообмен излучением?
3. Что называется интегральной плотностью потока полусферического излучения?
4. По какой формуле определяется полный поток излучения?
5. Как вычисляется спектральная (монохроматическая) плотность потока полусферического излучения?
6. Охарактеризуйте поглощательную, отражательную и пропускательную способности тела. Чему равна их сумма?
7. Какие тела называются абсолютно черными, абсолютно белыми и абсолютно прозрачными? Какие реальные тела наиболее близки к ним?
8. Какие вещества являются практически непрозрачными для тепловых лучей?
9. Что называется собственным излучением тела?
10. Что называется эффективным излучением тела?
11. По какой формуле определяется результирующее излучение?
12. Закон Планка и его графическое изображение.
13. Закон Вина.
14. Закон Стефана-Больцмана.
15. Коэффициент излучения абсолютно черного тела.
16. Чем отличается собственное излучение реальных тел от излу-чения абсолютно черного тела?
17. Понятие о степени черноты реального тела.
18. По какой формуле определяют излучение реальных тел?
19. Закон Кирхгофа.
20. Что следует из анализа уравнения закона Кирхгофа?
21. Закон Ламберта.

 

 

      4. 2. РАСЧЕТ ТЕПЛООБМЕНА ИЗЛУЧЕНИЕМ

 

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: