5. Теплопередача. 5. 1. Теплопередача через плоскую стенку. 5. 2. Теплопередача через цилиндрическую.     интенсивность передачи теплоты при теплопередаче характеризу-ется коэффициентом теплопередачи k

              5. ТЕПЛОПЕРЕДАЧА

  Теплопередачей называется теплообмен между двумя теплоноси-телями (движущимися средами) через разделяющую их твердую стенку. Теплопередача включает в себя перенос теплоты от более горячей жид-кости (газа) к стенке, теплопроводность в стенке, перенос теплоты от стенки к более холодной подвижной среде. Перенос теплоты от тепло-носителя к стенке и от стенки к теплоносителю может иметь характер теплоотдачи (совместное действие конвекции и теплопроводности) или радиационно-конвективного теплообмена (совместное действие конвек-ции, теплопроводности и теплового излучения).     

Примерами теплопередачи могут служить: передача теплоты от греющей воды к воздуху помещения через стенки нагревательных батарей центрального отопления, передача теплоты от дымовых газов к воде через стенки кипятильных труб в паровых и водогрейных котлах, передача теплоты от конденсирующегося пара к воде через стенки труб конденсатора, передача теплоты от нагретых газов к воде через стенку цилиндра двигателя внутреннего сгорания и т. д. Во всех рассматриваемых случаях стенка служит проводником теплоты и изготавливается из материала с высокой теплопроводностью.

В других случаях, когда требуется уменьшить потери теплоты, стенка должна быть тепловым изолятором и изготавливаться из материала с хорошими теплоизоляционными свойствами.  

     Интенсивность передачи теплоты при теплопередаче характеризу-ется коэффициентом теплопередачи k, который определяется как тепловой поток Q, передаваемый через единицу площади F стенки, в единицу времени при разности температур (Т_ж1 - Т_ж2) между теплоноси-телями в 1 К:

                                   k = Q / F(Т_ж1 – Т_ж2), Вт/(м²·К).                     (5. 1)

     

Величина, обратная коэффициенту теплопередачи, называется полным (общим) термическим сопротивлением теплопередачи:

 

                                                     R = 1/k.                                          (5. 2)

 

5. 1. ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ПЛОСКУЮ СТЕНКУ

Для расчета плотности теплового потокаq при теплопередаче через однослойную плоскую стенку   необходимо знатьтолщину стенки δ, ко-эффициент теплопроводности стенки λ, температуры теплоносителей Т₁ и Т₂ , коэффициенты теплообмена с обеих сторон стенки α ₁ и α ₂ (рис. 5. 1).

 

 

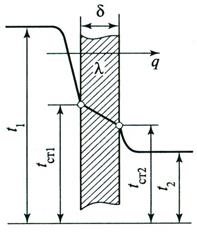
                           Рис. 5. 1. Схема теплопередачи через

                                однослойную плоскую стенку

              

При стационарном режиме теплообмена плотности теплового потока от первого теплоносителя к стенке, через стенку и от стенки ко второму теплоносителю одинаковы, т. е.

 

                 q = α ₁(Т_ж1 – Т_ст1) = λ (Т_ст1 – Т_ст2)/δ = α ₂(Т_cт2 – Т_ж2)        (5. 3)

 

или      Т_ж1 – Т_ст1 = q/α ₁; Т_ст1 – Т_ст2 = qδ /λ; Т_cт2 – Т_ж2 = q/α ₂.     (5. 4)

 

  Просуммировав уравнения (5. 4), получим:

 

                   q = (Т_ж1 – Т_ж2) /(1/α ₁ + δ /λ +1/α ₂) = k(Т_ж1 – Т_ж2).       (5. 5)

 

  Следовательно, значение коэффициента теплопередачи 

 

                                        k = 1/(1/α ₁ + δ /λ +1/α ₂),                             (5. 6)

 

Значение k всегда меньше наименьшего коэффициента теплоотдачи α.

Отсюда полное термическое сопротивление теплопередачи имеет вид:

                                    R = 1/k = 1/α ₁ + δ /λ +1/α ₂.                            (5. 7)

 

Из (5. 7) следует, что полное термическое сопротивление теплопередачи равно сумме отдельных, так называемых частных термических сопротивлений: термического сопротивления теплоотдачи (1/α ₁) со стороны теплоносителя с более высокой температурой; термического сопротивления теплопроводности стенки (δ /λ ); термического сопротивления теплоотдачи (1/α ₂) со стороны теплоносителя с более низкой температурой.   

Неизвестные температуры стенок Т_ст1 и Т_ст2 можно определить из уравнений (5. 4):

                                            Т_ст1 = Т_ж1 – q/α ₁;

                                                                                                                (5. 8)

                                             Т_ст2 = Т_ж2 + q/α ₂.

 

Если стенка состоит из n слоев толщиной  δ ₁, δ ₂, ..., δ _n, коэф-фициенты теплопроводности которых λ ₁, λ ₂, ..., λ _n, то с помощью аналогичных выкладок получим следующее выражение для коэф-фициента теплопередачи:

                                                            _n

                                      k = 1/(1/α ₁ + ∑ δ _i/λ _i +1/α ₂),                           (5. 9)

                                                           ^{i = 1}

а полное термическое сопротивление теплопередаче через многослойной плоскую стенку

                                                           _n

                                         R = 1/α ₁ + ∑ δ _i/λ _i +1/α ₂.                           (5. 10)

                                                          ^{i = 1}

 

 

  

5. 2. ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ЦИЛИНДРИЧЕСКУЮ

                                         СТЕНКУ

Для получения расчетной формулы плотности теплового потокаq при теплопередаче через однослойную цилиндрическую стенку   необ-ходимо знатьнаружный d₂ и внутренний d₁ диаметр цилиндра, коэффи-циент теплопроводности стенки цилиндра λ, температуры теплоносите-лей Т₁ и Т₂ , коэффициенты теплообмена с обеих сторон стенки α ₁ и α ₂ (рис. 5. 2).  

 

            Рис. 5. 2. Схема теплопередачи через однослойную

                                  цилиндрическую стенку

 

   При стационарном режиме теплообмена плотности теплового по-тока, приходящиеся на каждый метр длины цилиндрической стенки, от первого теплоносителя к стенке, через стенку и от стенки ко второму теплоносителю одинаковы. С учетом формулы (2. 41) тепловые потоки, приходящиеся на единицу длины цилиндрической стенки, можно выразить уравнениями:

 

                                     

                              q_l = Q/ℓ =α ₁π d₁(Т_ж1–Т_ст1);                          (5. 11)

 

                               q_l = π (Т_ст1–Т_ст2)/(1/ 2λ ) ln(d₂/d₁);                    (5. 12)

 

                                           q_l =α ₂π d₂(Т_ст2–Т_ж2).                              (5. 13)

 

Определим из уравнений (5. 11)-(5. 13) разности температур в явном виде:

                                          Т_ж1–Т_ст1 = q_l/α ₁π d₁;                               (5. 14)

 

                                   Т_ст1–Т_ст2 = q_l ln (d₂/d₁)/2π λ;                        (5. 15)                  

 

                                          Т_ст2–Т_ж2 = q_l /α ₁π d₁.                              (5. 16)

 

Просуммировав правые и левые части равенств (5. 14)-(5. 16), получим для теплового потока q_l следующую формулу:

 

q_l = π (Т_ж1–Т_ж2) / [1/α ₁d₁ +ln (d₂/d₁) /2λ +1/α ₂d₂] = k_l π (Т_ж1–Т_ж2), (5. 17)

 

откуда получим выражение для линейного коэффициента теплопередачи, который определяет тепловой поток, приходящийся на единицу длины цилиндрической стенки:

 

                            k_l = 1/ [1/α ₁d₁ + ln (d₂/d₁)/2λ + 1/α ₂d₂].              (5. 18)

 

Линейный коэффициент теплопередачи имеет размерность Вт/(м·К).

 

Из уравнений (5. 13)-(5. 15) получим выражения для определения неизвестных температур Т_ст1 и Т_ст2:

 

                                      Т_ст1 = Т_ж1 - q_l /α ₁π d₁;

                                                                                                              (5. 19)

                                      Т_ст2 = Т_ж2 + q_l /α ₂π d₂.

 

Если цилиндрическая стенка состоит из n слоев  и заданы (известны) диаметры каждого слоя, коэффициенты теплопроводности каждого слоя, температуры теплоносителей и коэффициенты теплообмена с обе-их сторон многослойной стенки, то линейный коэффициент теплопе-редачи определяется по формуле:

                                            _n

                 k_l = 1/ [1/α ₁d₁ + ∑ (1/2λ _i) ln (d_{i + 1}/d_i)  +1/α ₂d_{n +1}].          (5. 20)                                               

                                           ^{i = 1}

  Температура поверхностей, соприкасающихся с теплоносителем, определяется из формул, аналогичных уравнениям (5. 18):

 

                                       Т_ст1 = Т_ж1 - q_l /α ₁π d₁;

                                                                                                              (5. 21)

                                     Т_{ст n+1} = Т_ж2 + q_l /α ₂π d_n+1.

⇐ Предыдущая17181920212223242526Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: