 |
Теория проверки статистических гипотез
|
|
|
|
Важное место в практике врача занимает процесс сравнения. По сути, вся его деятельность – это постоянное сравнение: больного со здоровым, состояния организма до и после лечения, эффективности диагностических или лечебных методов и т.д. При этом надо учитывать, что если врачу важны результаты отдельного больного, то общество в целом интересуют эффекты на популяционном уровне (на уровне генеральной совокупности), т.е. поможет ли новый препарат всем больным данной нозологии, сколько процентов из всех больных правильно диагностируется с помощью нового метода, как часто встречается то или иное заболевание в различных популяциях.
Как правило, ответить на эти вопросы можем, лишь опираясь на выборочные данные, на выборку. Мы уже указывали, что выборочные данные не совсем точно отражают истинное положение дел - делая по ним то или иное заключение, надо учитывать, что есть вероятность ошибиться и эта вероятность может быть достаточно большой. Исследователь сам должен решить устраивает ли его такая ошибка, принимать или не принимать эти результаты.
В связи с этим в статистике выработана специальная процедура, которая носит название проверка статистических гипотез. Т.е. при наличии выборочных данных предварительно высказываются предположения – гипотезы. Различают нулевую Н(0) и альтернативную Н(1) гипотезы. Нулевая гипотеза содержит предположение о равенстве (отсутствии эффекта), о соответствии, о независимости. Например, о равенстве средних значений гемоглобина у жителей двух различных районов (т.е. эффект от места жительства отсутствует). Или - распределение случайной величины соответствует нормальному закону. Или - заболеваемость не зависит от профессиональной принадлежности.
|
|
|
Для исследователя больший интерес представляет альтернативная гипотеза, поскольку она соответствует целям большинства исследований – найти различия, зависимости, несоответствия.
Максимальная вероятность ошибки, которую может себе позволить исследователь, принимая альтернативную гипотезу (т.е. отклонив нулевую) называется уровнем значимости иобозначается буквой α (альфа). Эту ошибку также называют ошибкой I рода.
Уровень значимости – это вероятность того, что мы сочли различия существенными, в то время как они на самом деле случайны.
Уровень значимости α задается самим исследователем, исходя из сути решаемой проблемы. В медико-биологических задачах обычно принимают α =0,05 (5%), 0,01(1%) или 0,001 (0,1%).
При α =0,05 если мы примем альтернативную гипотезу, то в более чем 95% случаях гипотеза будет верна, а в менее чем 5% - ошибочна.
Также может возникнуть ошибка, если мы принимаем нулевую гипотезу, в то время как она не верна, другими словами, не находим существующие различия. Эта ошибка II рода, ее вероятность обозначается буквой β. Величина (1- β) называется мощностью критерия – это способность критерия найти различия там, где они заведомо существуют.
Для принятия или отклонения гипотезы используются статистические критерии. Они подразделяются на два вида:
параметрические критерии - используются если
• признаки количественные
• совокупности имеют нормальное распределение
• дисперсии совокупностей не сильно различаются
непараметрические критерии - используются если
• признаки количественные, но распределение не соответствует нормальному
• или если распределение неизвестно и нельзя его проверить (т.е. n<30)
• или если признаки качественные
Выбор критерия определяется также тем, являются ли сравниваемые выборки зависимыми или независимыми.
|
|
|
Независимые выборки – это выборки, состоящие из разных объектов, причем значения случайной величины в одной выборке не зависят от его значений в другой выборке. Например, сравниваются выборки, состоящие из больных и здоровых, или одна группа принимает один препарат, вторая группа – другой, выборки мужчин и женщин, строителей и шахтеров и т.д.
Зависимые выборки состоят из одних и тех же объектов, исследованных «до» и «после». Например, гемоглобин у больных до и после лечения, ЧСС спортсменов до и после физической нагрузки, АД у гипертоников в динамике по годам и т.д.
Гипотезы можно проверить двумя путями
I алгоритм
• сформулировать нулевую и альтернативную гипотезы
• выбрать уровень значимости α
• выбрать статистический критерий для проверки гипотезы
• далее на основании имеющихся выборочных данных определить какую ошибку р мы совершим, если отвергнем нулевую гипотезу, т.е. примем Н(1) (р означает достигнутый уровень значимости)
• если р ≤ α то принимается альтернативная гипотеза (нулевая отвергается)
• если р > α, то принимается нулевая гипотеза
Вычисление р -уровня задача непростая, но она реализована в большинстве компьютерных программ статистической обработки данных. Поэтому данный алгоритм используется при наличии таких программ.
В противном случае можно воспользоваться другим алгоритмом, который менее желателен, но иногда более доступен.
II алгоритм
• выбрать уровень значимости α
• сформулировать нулевую и альтернативную ей гипотезы
• выбрать статистический критерий для проверки гипотезы
• вычислить значение критерия
• сравнить вычисленное значение критерия с его критическим значением для заданного уровня значимости (критическое значение находим по специальным таблицам с заданным уровнем значимости)
• на основе сравнения вычисленного и критического значений критерия принимается Н(0) или Н(1)
| В таблицах критических значений даны односторонние и двусторонние критерии. Здесь дело в том, что при сравнении двух совокупностей могут выдвигаться направленные и ненаправленные альтернативные гипотезы. Ненаправленная гипотеза предполагает, что значения переменной в первой совокупности отличны от значений во второй без уточнения в меньшую или большую сторону, например, «содержание белка в крови больных гепатитом отличается от нормы». В этом случае используются двусторонние критерии. Направленная альтернативная гипотеза уточняет направление отличий, например, «содержание белка в крови при гепатите больше нормы», в этом случае используются односторонние критерии. |
|
|
|
Прежде чем приступить к рассмотрению различных методов проверки статистических гипотез необходимо уточнить, что понимается при групповых исследованиях под терминами «отличается» - «не отличается», «одинаково» - «не одинаково», «изменилось» - «не изменилось».
Две совокупности считаются не отличающимися по данной величине, если распределение этой величины в обеих совокупностях одинаково (на рисунке 14 рост девочек не отличается от роста мальчиков).
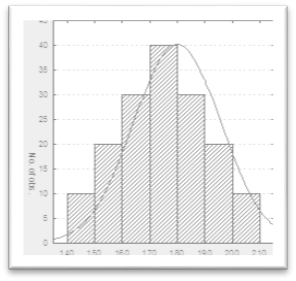

Рисунок 14
Считается, что в совокупности не произошли изменения, если среднее значение всех изменений равно нулю ( на рисунке 15 изменение веса по группе в среднем равно нулю).
В таблице приведены данные пульса до и после пробежки у пяти испытуемых. Видно, что в среднем изменение пульса равно нулю.
| Пульс до, уд/мин | ||||||
| Пульс после, уд/мин | ||||||
| Разница, уд/мин | +10 | +5 | -5 | -5 | -5 | ∑=0 |
| похудели |
| поправились |
| Эффект = 0 |
Рисунок 15
|
|
|


