 |
Анализ относительных величин
|
|
|
|
Относительные величины особенно часто используются для более углубленного анализа общественного здоровья и деятельности учреждений здравоохранения, а также деятельности медицинского работника. Они применяются для изучения совокупности, которая характеризуется, главным образом, качественными номинальными признаками, типа «болеет - не болеет», «есть – нет», «городской - сельский» и т.д.. В этом случае исследователя интересует доля объектов с заданными свойствами в некоторой совокупности.
| Например, в районе А в текущем году было зарегистрировано 500 случаев инфекционных заболеваний, из них: эпидемического паротита - 60 случаев; кори - 100 случаев; прочих инфекционных заболеваний - 340 случаев. Структура инфекционных заболеваний выглядит следующим образом: вся совокупность - 500 случаев инфекционных заболеваний принимается за 100 %, составные части определяются как искомые. Удельный вес случаев эпидемического паротита составит: 60 x 100% / 500 = 12% и т.д. |
Удобно относительные величины представлять в виде круговых диаграмм
Рисунок 19
Относительная частота (доля) р определяется следующим образом:
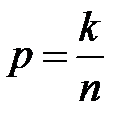 (может быть в %),
(может быть в %),
где k – число случаев интересующего признака, n – объем выборки.
Поскольку р определяется по выборке, она отражает генеральную долю с некоторой ошибкой.
Стандартная ошибка доли

Иногда при малых выборках получаются так называемые нулевой или стопроцентный эффекты, т.е. объекты с интересующим нас признаком или вообще не встречаются или встречаются в 100% случаев. Вряд ли такие выводы можно перенести на всю генеральную совокупность, несмотря на то, что стандартная ошибка при этом буде равна нулю. Для статистической обработки нулевого (или 100%) эффекта вводится скорректированное значение доли
|
|
|
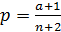
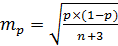
где a – число объектов с заданными свойствами.
Пример. Выборочные данные по заболеваемости гепатитом среди наркоманов приведены в таблице. Из нее видно, что частота составляет 6 человек из 6, т.е. 100%. .
Стопроцентный эффект с поправкой составит
Доля лиц без гепатита среди наркоманов (нулевой эффект)
|
Сравнение относительной частоты встречаемости признака в различных независимых совокупностях – одна из наиболее часто решаемых задач медицинских исследований. Нулевой гипотезой при этом является предположение о равенстве двух генеральных долей. Для проверки можно использовать критерий Стъюдента:
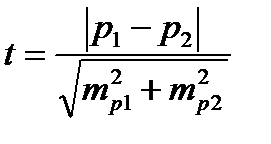
Критическое значение t-критерия находится по таблице для заданного уровня значимости и числа степеней свободы f = n1 + n2 – 2 (Приложение 2 ).
Если tвыч ≥ tкрит, то принимается альтернативная гипотеза, если tвыч < tкрит – то нулевая.
Доверительный интервал
Любая выборка дает лишь приближенное представление о генеральной совокупности, и все выборочные статистические характеристики (средняя, мода, дисперсия…) являются некоторым приближением или говорят оценкой генеральных параметров, которые вычислить в большинстве случаев не представляется возможным из-за недоступности генеральной совокупности.

Рисунок 20
Но можно указать интервал, в котором с определенной долей вероятности лежит истинное (генеральное) значение статистической характеристики. Этот интервал называется доверительный интервал (ДИ).
Так генеральное среднее значение с вероятностью 95% лежит в пределах
от 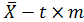 до
до  ,
,
|
|
|
где t – табличное значение критерия Стъюдента для α =0,05 и f=n-1
Может быть найден и 99% ДИ, в этом случае t выбирается для α =0,01.
Какое практическое значение имеет доверительный интервал?
· Широкий доверительный интервал показывает, что выборочная средняя неточно отражает генеральную среднюю. Обычно это связано с недостаточным объемом выборки, или же с ее неоднородностью, т.е. большой дисперсией. И то и другое дают большую ошибку среднего и, соответственно, более широкий ДИ. И это является основанием вернуться на этап планирования исследования.
· Верхние и нижние пределы ДИ дают оценку, будут ли результаты клинически значимы
Остановимся несколько подробнее на вопросе о статистической и клинической значимости результатов исследования групповых свойств. Вспомним, что задачей статистики является обнаружение хоть каких-либо отличий в генеральных совокупностях, опираясь на выборочные данные. Задачей клиницистов является обнаружение таких (не любых) различий, которые помогут диагностике или лечению. И не всегда статистические выводы являются основанием для клинических выводов. Так, статистически значимое снижение гемоглобина на 3 г/л не является поводом для беспокойства. И, наоборот, если какая-то проблема в организме человека не имеет массового характера на уровне всей популяции, это не основание для того, чтобы этой проблемой не заниматься.
Это положение рассмотрим на примере. Исследователи задались вопросом, не отстают ли в росте от своих сверстников мальчики, перенесшие некое инфекционное заболевание. С этой целью было проведено выборочное исследование, в котором приняли участие 10 мальчиков, перенесших эту болезнь. Результаты представлены в таблице
Из этих расчетов следует, что выборочный средний рост мальчиков 10 лет, перенесших некое инфекционное заболевание, близок к норме (132,5 см). Однако нижний предел доверительного интервала (126,6 см) свидетельствует о наличии 95% вероятности того, что истинный средний рост этих детей соответствует понятию «низкий рост», т.е. эти дети отстают в росте.
В этом примере результаты расчетов доверительного интервала клинически значимы. |
|
|
|




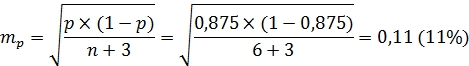
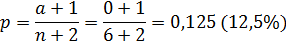
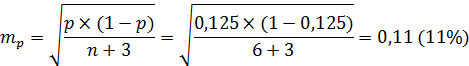
 (см)
(см)