Геометрический смысл знака трехчлена прямой

Каждая прямая плоскости разделяет эту плоскость на две части, называемые полуплоскостями. Две точки одной и той же полуплоскости лежат по одну сторону от данной прямой. Любые две точки, принадлежащие различным полуплоскостям, лежат по разные стороны от прямой. Как аналитически, то есть по уравнению прямой и координатам точек определить, лежат эти точки в одной или в разных полуплоскостях относительно данной прямой?

Относительно аффинной системы координат прямая задана уравнением , где .

Обозначим – трехчлен прямой.

Для точек и , не лежащих на прямой , будем иметь .

Точки и лежат по разные стороны от прямой тогда и только тогда, когда отрезок пересекает прямую в некоторой точке .

Так как точка лежит между и , то и , .

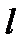Точка лежит на прямой , поэтому . Отсюда получаем и , а значит и разных знаков.

Таким образом, две точки и лежат по разные стороны от прямой тогда и только тогда, когда значения трехчлена прямой для координат этих точек и разных знаков.

Имеем геометрический смысл знака трехчлена:

Каждое из неравенств определяет полуплоскость с границей .

 

Расстояние от точки до прямой

Пусть на плоскости относительно прямоугольной системы координат 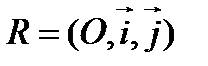прямая задается уравнением , где .

Расстояние от точки 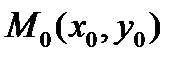до прямой равняется длине перпендикуляра , проведенного из к прямой .

Так как , то .

. Так как равен либо , либо , то получаем

. Учитывая, что 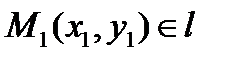, то есть , получаем формулу для вычисления расстояния от точки до прямой

.

 

Взаимное расположение двух прямых на плоскости

Относительно аффинной системы координат прямые и задаются уравнениями

Для каждой прямой можно найти точку, принадлежащую этой прямой, и направляющий вектор

, если ;

, если

1.

Прямые совпадают тогда и только тогда, когда в их общих уравнениях коэффициенты и свободные члены пропорциональны.

2. .

Прямые параллельны тогда и только тогда, когда в их общих уравнениях коэффициенты пропорциональны, но не пропорциональны свободным членам.

3.

Прямые пересекаются в точке тогда и только тогда, когда в их общих уравнениях коэффициенты не пропорциональны.

 

Угол между прямыми

Углом между прямыми и 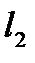называется величина того из четырех вертикальных углов, образованных этими прямыми, который не превосходит остальные углы. Таким образом, угол между прямыми может принимать значения от 0 до .

Иногда удобно угол между прямыми считать направленным. Угол между прямыми и , заданными в указанном порядке, будем считать положительным, если поворот от к по этому углу совершается против часовой стрелки. В противном случае угол будем считать отрицательным.

Пусть на плоскости относительно прямоугольной системы координат 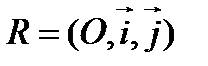прямые и задаются уравнениями

Тогда , .

Угол 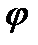между прямыми и равен тогда и только тогда, когда направляющие векторы прямых ортогональны и, следовательно, .

Если угол между прямыми отличен от , то он однозначно определяется по значению его тангенса.

Заметим, что тангенс направленного угла между прямыми равен тангенсу направленного угла между направляющими векторами этих прямых: .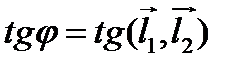

Как вычислить тангенс направленного угла между векторами и ?

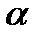Пусть и направленные углы между вектором и направляющими векторами прямых. Для направленного угла между векторами 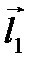и имеем .

Для вычисления найдем и :

.

.

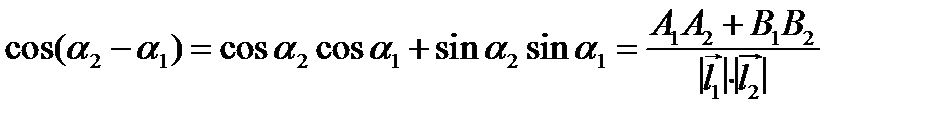Таким образом, .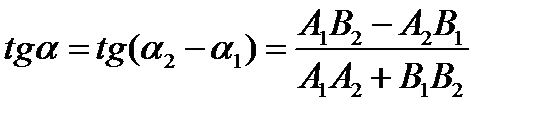

Возможны случаи

а) не параллельны оси )

, где и – угловые коэффициенты прямых и .

б) , ( параллельна, а не параллельна оси ).

.

в) ( параллельна, а не параллельна оси ).

.

г) , (прямые параллельны оси ).

 

 

Лекция 4. Конические сечения: эллипс, гипербола, парабола

Эллипс

 

О п р е д е л е н и е. Эллипсом называется множество всех точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами:

.

Чтобы найти уравнение эллипса, нужно удобным образом выбрать систему координат.

, где – середина отрезка , . Тогда .

Под уравнением фигуры понимаем уравнение, которому удовлетворяют координаты любой точки, принадлежащей фигуре, и не удовлетворяют координаты точек, не принадлежащих фигуре. Поэтому, вывод уравнения эллипса состоит из двух этапов: сначала находим уравнение, которому удовлетворяют координаты любой точки эллипса, затем показываем, что если координаты точки удовлетворяют этому уравнению, то точка принадлежит эллипсу.

I. . Используя формулы вычисления расстояния между точками, получим уравнение, которое приводится к виду , где обозначено .

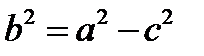II. Пусть координаты точки 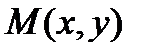удовлетворяют уравнению . Покажем, что точка принадлежит эллипсу, то есть .

Непосредственным вычислением получаем .

Из уравнения, которому удовлетворяют координаты точки , следует . Кроме того, . Поэтому, имеем и .

Аналогично находим .

Тогда и значит, точка принадлежит эллипсу.

Из I и II следует, что – уравнение эллипса – каноническое уравнение эллипса и значит эллипс – линия второго порядка.

Исследование формы эллипса

1. . То есть являются осями симметрии, а центром симметрии.

2. . Так как , то все точки эллипса находятся внутри прямоугольника, определяемого прямыми .

3. Определяя точки пересечения эллипса с произвольной прямой , проходящей через начало системы координат, получим систему уравнений .

Тогда , то есть система всегда имеет два решения, а значит, любая прямая, проходящая через начало координат, пересекает эллипс в двух точках, симметричных относительно . В частности

.

Точки называются вершинами эллипса, 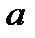– большой полуосью, – малой полуосью.

Важно помнить, что фокусы эллипса лежат на его большой оси.

4. Для точек эллипса, находящихся в первой координатной четверти, имеем . Таким образом, если возрастает от 0 до , то 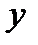убывает от до 0.

5. Эксцентриситетом эллипса называется число . Таким образом, эксцентриситет эллипса меньше 1.

Имеем . Отсюда 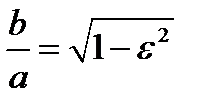. Для системы эллипсов с одной и той же большой осью ( постоянно) видим, что с увеличением эксцентриситета уменьшается малая ось, то есть эллипс становится более сплюснутым. Когда получаем и эллипс становится окружностью.

 

Гипербола

О п р е д е л е н и е. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами:

.

По аналогии с эллипсом можно вывести каноническое уравнение гиперболы: , где обозначено .

Исследование формы гиперболы

1. 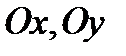– оси симметрии, – центр симметрии гиперболы.

2. . Из уравнения гиперболы следует, что , то есть все точки гиперболы находятся вне полосы, определяемой прямыми .

3. Поиск точек пересечения гиперболы с – произвольной прямой, проходящей через начало системы координат, сводится к решению уравнения . Таким образом, если , то прямая пересекает гиперболу в двух точках, симметричных относительно начала системы координат.

Если , то прямая не пересекает гиперболу.

При этом и, следовательно, .

Получаем, что прямая не пересекает гиперболу, если модуль её углового коэффициента не меньше, чем модули угловых коэффициентов прямых и . Прямые и называются асимптотами гиперболы.

Ось пересекает гиперболу в точках и 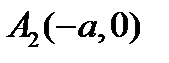– вершины гиперболы. Ось называется вещественной осью.

Ось не имеет с гиперболой общих вещественных точек и называется мнимой осью гиперболы.

4. Прямая , , пересекает гипеболу в точке , а асимптоту в точке . Расстояние от точки до гиперболы меньше, чем расстояние . Видим, что при расстояние от точки до гиперболы стремится к нулю. То есть по мере удаления от мнимой оси точки гиперболы неограниченно приближаются к соответствующей асимптоте.

5. Эксцентриситетом гиперболы называется число 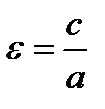. Таким образом, эксцентриситет гиперболы больше .

Имеем Таким образом, для системы гипербол с общими вещественными вершинами ( постоянно) с возрастанием эксцентриситета ветви гипербол все более удаляются от вещественной оси.

 

Парабола

О п р е д е л е н и е. Параболой называется множество всех точек плоскости, расстояние от которых до заданной прямой, называемой директрисой, равно расстоянию до заданной точки – фокуса: .

Расстояние от фокуса до директрисы называется фокальным параметром параболы.

По аналогии с эллипсом и гиперболой выводится каноническое уравнение параболы: .

Изучение формы параболы

1. – ось симметрии параболы.

2. Точки принадлежат параболе.

3. Поиск точек пересечения произвольной прямой проходящей через начало системы координат с параболой сводится к решению к решению уравнения . Таким образом, если прямая отлична от оси (), то она пересекает параболу в двух различных точках. Ось пересекает параболу в одной точке.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: