 |
Группа аффинных преобразований, её подгруппы. Эрлангенская программа Ф. Клейна
|
|
|
|
Множество А всех аффинных преобразований плоскости является группой относительно композиции преобразований. Основным инвариантом этой группы является простое отношение трех точек прямой.
Фигуры 
и 
называются аффинно-эквивалентными, если они эквивалентны относительно группы аффинных преобразований. Примерами аффинно-эквивалентных фигур являются любые два треугольника, любые два эллипса, две гиперболы, две параболы.
Примерами подгрупп группы А аффинных преобразований являются:
· 
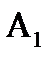– множество всех аффинных преобразований первого рода. К инвариантам группы А добавляется еще один инвариант – ориентация плоскости.
· Р – группа подобий. К инвариантам группы А добавляется инвариант – величина угла.
· 
– группа движений. К инвариантам группы подобий добавляется инвариант – расстояние.
· 
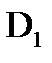– группа движений первого рода. К инвариантам группы движений добавляется инвариант – ориентация плоскости.
Приведите ещё примеры подгрупп группы А и отметьте изменения в числе инвариантов.
Можно заметить, что чем уже группа, тем шире список инвариантов.
XIX век явился периодом бурного развития геометрических учений. Еще в начале этого столетия было распространено глубокое убеждение в уникальности евклидовой геометрии, так что выражение «геометрия» полностью отождествлялось с понятием «евклидова геометрия». Однако к рубежу 20-х, 30-х годов появляются первые работы Н.И. Лобачевского, Я. Бойяи, посвященные гиперболической геометрии. В конце 60-х годов была опубликована замечательная речь Римана, постулирующая равноправность трех «геометрий постоянной кривизны»: евклидовой, гиперболической и эллиптической.
Бурное развитие геометрии поставило на повестку дня вопрос об общем описании всех рассматриваемых математиками «геометрических систем».
|
|
|
В 1872 году 23-летний Феликс Клейн, вступая в должность профессора кафедры математики Эрлангенского университета, прочел открытую лекцию на тему «Сравнительное обозрение новейших геометрических исследований». Лекция Клейна за ясность позиции автора и открываемые широкие горизонты дальнейшего прогресса геометрии почти сразу получила в научном мире почетное звание «Эрлангенская программа». Идея Клейна состоит в следующем:
Каждой группе преобразований соответствует своя геометрия – теория, которая изучает свойства фигур, сохраняющиеся при всех преобразованиях данной группы.
Таким образом, имеем многообразие геометрий: аффинная геометрия, соответствующая группе аффинных преобразований, геометрия движений, геометрия подобий и т. д.
Лекция 5. Движения пространства, их классификация
Движения пространства
По аналогии с плоскостью определим движения пространства.
О п р е д е л е н и е. Параллельным переносом 
на вектор 
называется отображение пространства в себя, при котором каждой точке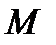 
ставится в соответствие точка 
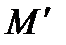такая, что 
.
Докажите, что параллельный перенос является преобразованием пространства.
Найдите формулы параллельного переноса, покажите, что параллельный перенос является движением первого рода. Определите неподвижные точки и неподвижные прямые при параллельном переносе.
О п р е д е л е н и е. Поворотом 
вокруг прямой 
на угол 
называется отображение пространства в себя, при котором каждой точке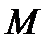 
ставится в соответствие точка 
, полученная в результате поворота 
плоскости, проходящей через точку 
перпендикулярно прямой 
и пересекающей 
в точке 
.
Найдите формулы поворота вокруг оси аппликат прямоугольной системы координат. Покажите, что поворот вокруг прямой является движением первого рода. Определите неподвижные точки и неподвижные прямые этого преобразования.
|
|
|
О п р е д е л е н и е. Винтовым движением называется композиция поворота вокруг прямой и параллельного переноса на вектор, параллельный оси поворота: 
.
Сравнив число неподвижных точек и прямых, можно сделать вывод, что винтовое движение является движением первого рода, отличным от параллельного переноса и поворота вокруг прямой.
О п р е д е л е н и е. Отражением 
от плоскости 
называется отображение пространства в себя, при котором каждой точке пространства ставится в соответствие точка, симметричная ей относительно 
.
Точки симметричные относительно плоскости определяются аналогично точкам, симметричным относительно прямой.
Найдите формулы отражения относительно плоскости 
прямоугольной системы координат. Покажите, что отражение от плоскости является движением второго рода. Определите неподвижные точки и неподвижные прямые этого преобразования.
О п р е д е л е н и е. Скользящим отражением называется композиция отражения от плоскости и параллельного переноса на вектор, параллельный этой плоскости: 
.
Сравнив число неподвижных точек и прямых, можно сделать вывод, что скользящее отражение является движением второго рода, отличным от отражения от плоскости.
О п р е д е л е н и е. Поворотным отражением называется композиция отражения от плоскости и поворота вокруг прямой, перпендикулярной этой плоскости: 
.
Сравнив число неподвижных точек и прямых, можно сделать вывод, что поворотное отражение является движением второго рода, отличным от отражения от плоскости и от скользящего отражения.
Можно показать, что других движений пространства не существует.
По аналогии с плоскостью можно показать, что
1. Композиция отражений от двух пересекающихся плоскостей есть поворот вокруг пересечения плоскостей, на угол, равный удвоенному углу между плоскостями.
2. Композиция отражений от двух параллельных плоскостей есть параллельный перенос на вектор, ортогональный плоскостям, длина которого равна удвоенному расстоянию между плоскостями.
3. Всякое движение пространства является композицией не более четырех отражений от плоскотей.
|
|
|
Представьте каждое из шести движений пространства в виде композиции отражений от плоскостей.
Литература
1. Атанасян, Л.С. Геометрия, Ч. 2 [Текст] / Л.С. Атанасян, В.Т. Базылев. − М.: Просвещение, 1987. – 351 с.
2. Базылев, В.Т. Геометрия, Ч. 2 [Текст] / В.Т. Базылев, К.И. Дуничев. – М.: Просвещение, 1975. − 367 с.
3. Горшкова, Л.С. Проективная геометрия [Текст] / Л.С. Горшкова, В.И. Паньженский, Е.В. Марина. – М.: Изд. ЛКИ, 2007. – 168 с.
4. Гуревич, Г.Б. Проективная геометрия [Текст] / Г.Б. Гуревич. − М., 1960. – 317 с.
5. Ефимов, Н.В. Высшая геометрия [Текст] / Н.В. Ефимов. – М.: Наука, 1978. – 280 с.
6. Каюмов, О.Р. Проективные свойства фигур: Учебное пособие [Текст] / О.Р. Каюмов. – Омск:Изд-во ОмГПУ, 2003.
7. Комиссарук, А.М. Проективная геометрия в задачах [Текст] / А.М. Комиссарук. – Минск, 1971. – 319 с.
8. Матвиевская, Г.П. Альбрехт Дюрер – ученый [Текст] / Г.П. Матвиевская. – М.: Наука, 1987. – 240 с.
9. Певзнер, С.Л. Проективная геометрия [Текст] / С.Л. Певзнер. − М.: Просвещение, 1980. – 216 с.
10. Прасолов, В.В. Задачи по планиметрии, Ч. 2 [Текст] / В.В. Прасолов. – М., 1991. – 239 с.
11. Проективные факты в решении элементарно-геометрических задач. Методическая разработка [Текст] / Сост. В.П. Толстопятов. – Екатеринбург:УрГПУ, 2000. – 42 с.
12. Раушенбах, Б.В. Системы перспективы в изобразительном искусстве [Текст] / Б.В. Раушенбах. – М.: Наука, 1986. – 255 с.
13. Четверухин, Н.Ф. Проективная геометрия [Текст] / Н.Ф. Четверухин. – М.: Просвещение, 1953. − 367 с.
14. Щербаков, Р.Н. От проективной геометрии к неевклидовой [Текст] / Р.Н. Щербаков, Л.Ф. Пичурин. – М., 1979. – 158 с.
Толстопятов Владимир Павлович
Геометрия
Курс лекций, 1 семестр
Учебное пособие
Подписано в печать Формат 60х84/16
Бумага для множительных аппаратов
Усл. печ. л. 6 Тираж 150 экз. Заказ
Уральский государственный педагогический университет
Екатеринбург, пр. Космонавтов, 26
|
|
|
