V. Антиферро- и ферримагнетизм

 

Рис. 5.1. Антиферромагнитное упорядочение в MnO.

Антиферромагнетики.

В антиферро- и ферримагнетиках обменный интеграл J<0 реализуется антипараллельная ориентация спина. В отличие от ферро- и ферримагнетиков, антиферромаг-нетики не обладают результирующей или остаточной намагниченностью. Минимум энергии антиферромагнетика в отсутствие магнитного поля достигается тогда, когда спины полностью компенсируются, как схематично показано на рис. 5.1 для MnO. Намагниченность у них возникает при наложении внешнего поля. К антиферромагнетикам относятся элементы: Cr, Mn (в a-фазе), ряд редкоземельных металлов, а также многочисленные соединения, в состав которых, как правило, входит один или несколько химических переходных или редкоземельных элементов. Из соединений большую группу составляют оксиды, сульфиды, теллуриды, селениды,галогениды и др. Свойства некоторых из них приведены в таблице 5.1.

 

Таблица 5.1. Антиферромагнетики

Вещество	Решетка	Температура Нееля, ТN (K)	Температура Кюри-Вейса, θ (К)	θ/TN	χ(0)/χ(TN)
MnO	гцк			5.3	2/3
MnS	гцк			3.3	0.82
MnTe	гекс. слоевая			2.25
FeMn
IrMn
FeF2	оц тетр.			1.24	0.76
FeF2	оц тетр			1.48	0.72
FeCl2	гекс. слоевая			2.0	<0.2
FeO	гцк			2.9	0.8
CoCl2	гекс. слоевая		38.1
CoO	гцк			1.14
NiCl2	гекс. слоевая		68.2	1.37
NiO	гцк		~2000	~4
Cr	оцк

 

Из дальнейшего рассмотрения будет видно, что аналогично ферромагнетикам, антиферромагнетики подчиняются закону Кюри-Вейса (4.4), с критической температурой, T_N, называемой температурой Нееля перехода из антиферромагнитного состояния в парамагнитное.

 

Ферримагнетики.

Ферримагнетики (оксидные ферримагнетики называют ферритами) также имеют две магнитных подрешетки с противоположно направленными спинами, которые, однако, в отличие от антиферромагнетиков, скоменсированы неполностью. Наиболее исследованы и нашли широкое применение ферриты, например, MeO*Fe₂O₃, где Me=(Mg²⁺, Zn²⁺, Cu²⁺, Ni²⁺, Fe²⁺, Mn²⁺) или Ме²⁺[Fe²⁺Fe³⁺]O₄, имеющие кубическую структуру типа шпинель или гранат. В элементарной ячейке магнетита, Fе²⁺[Fe²⁺Fe³⁺]O₄, (рис.5.2), 8 ионов Fe³⁺, занимающие тетраэдрические положения, и 8 ионов Fe³⁺, занимающие октаэдрические положения имеют противоположную ориентацию спинов и поэтому их моменты компенсируются. Магнетизм обусловлен 8-ью электронами Fe²⁺, занимающими тетраэдрические положения, как схематично показано ниже:

Рис. 5.2. Ферримагнитное упорядочение в магнетите Fе2+[Fe2+Fe3+]O4.

S=5/2 ­­­­...­ ­­...­ S=2 октаэдрические положения

8Fe³⁺ 8Fe²⁺

 

¯¯¯¯...¯ тетраэдрические положения

8Fe³⁺

 

Магнитные свойства некоторых ферримагнетиков приведены в таблице 5.2.

 

Таблица 5.2. Ферримагнетики.

Вещество	Намагниченность Ms (Гс)	n(0K)=μ/μB	TC, K
Т = 300 К	Т= 0К
MnAs			3.4
MnBi			3.52
MnSb		-	3.5
CrO2		-	2.03
MnOFe2O3		-	5.0
FeOFe2O3		-	4.1
NiOFe2O3		-	2.4
CuOFe2O3		-	1.3
MgOFe2O3		-	1.1
EuO	-		6.8
Y3Fe5O12			5.0

 

Значительную часть ферримагнетиков составляют диэлектрические и полупроводниковые ионные кристаллы, содержащие магнитные ионы различных элементов и одного элемента, но находящихся в разных кристаллографических позициях (в неэквивалентных узлах кристаллографической решетки).

 

Условие ферримагнетизма.

Представим себе кристалл, имеющий две магнитных подрешетки А и В с антипараллельными (­¯) магнитными моментами. В этом случае:

B _A=-l M _A-m M _B; B _В=-m M _A-n M _B, l,m,n>0. (5.1)

U= -1/2(B _A M _A+ B _B M _B)=1/2lM_A²+m M _A M _B+1/2nM_B². (5.2)

Энергия ниже, когда M _A­¯ M _B. Энергия» 0, когда M_A=M_B=0. ­¯-ное состояние устойчиво, когда

mM_AM_B>1/2(lM_A²+nM_B²). (5.3)

Температура Нееля, Кюри-Вейса и восприимчивость ферримагнетиков.

Определим константы Кюри C_A и C_B для подрешеток А и В. Для простоты пренебрежем всеми взаимодействиями, кроме ­¯-ного между А- и В- подрешетками: B _A=-m M _B; B _B=-m M _A;

В приближении среднего поля

M_AT=C_A(B_a-mM_B); M_BT=C_B(B_a-mM_A). (5.4)

При B_a =0 эта система уравнений становится однородной относительно M_A и M_B и имеет решение, если

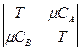=0. (5.5)

Отсюда ферромагнитная температура Кюри дается выражением

T_c=m(C_AC_B)^1/2. (5.6)

Решая (5.4), мы получим восприимчивость при T>T_с

c=(M_A+M_B)/B_A=((C_A+C_B)T-2mC_AC_B)/(T²-T_c²). (5.7)

При C_A=C_B =C – антиферромагнетизм.

Антиферромагнетик – это скомпенсированный ферримагнетик. Пример: MnO (рис.5.1), где спины Mn²⁺ скомпенсированы. Переход из антиферромагнитной фазы в парамагнитную происходит при температуре Нееля, Т_N:

T_N=mC, c=(2CT-2mC²)/(T²-(mC)²), т.е. c=2C/(T+T_N) при T>T_N. (5.8а)

В действительности экспериментальные значения укладываются в зависимость

c=C/(T+q) при T>T_N. (5.8б)

Температуру q называют температурой Кюри-Вейса. Отношение q/T_N ~ 1 ¸ 5 и часто отличается от 1 (см. также таблицу 5.2). Качественное сопоставление хода температурных зависимостей магнитных восприимчивостей для парамагнетиков, ферромагнетиков и антиферромагнетиков приведено на рис.5.3.

 

Восприимчивость антиферромагнетиков ниже температуры Нееля.

Рассмотрим два случая, когда внешнее поле перпендикулярно и параллельно полному спину: 1) B_a ^ S и 2) B_a çç S.

Рис. 5.3. Температурная зависимость магнитной восприимчивости парамагнетиков, ферромагнетиков, антиферромагнетиков.

При T>T_N c»const (т.е. практически не зависит от взаимной

ориентации поля и спинов - парамагнитное поведение).

При T<T_N, если B_a ^ S, то можно считать, что в этом случае плотность энергии при |M_A| = |M_B| = M, то

-2U= M _A B _A +M _B B _B,

B _A= B _a-m M _B B _B= B _a-m M _A. Тогда -2U= M _A B _a- M _A m M _B+ M _B B _a- M _B m M _A. Т.е. -2U= B _a(M _A+ M _B)-2m M _A M _B, или

U = m M _A M _B -1/2 B_a (M _A +M _B) @ mM²[1-1/2(2j)²]-2B_aMj/2, (5.9)

где 2j -угол между S _A и S _B. Минимум энергии будет при dU/dj=0=4mM²j - B_aM

или в устойчивом состоянии j=B_a/4mM. (5.10)

Т.о. c_^=2Mj/B_a=1/2m. (5.11)

В ||-ной ориентации M_S = M_A + M_B = 0 при Т = 0, поэтому восприимчивость при T=0K равна нулю c_êê(0)=0. Эксперимен-тальная зависимость c_^ и c_êê для MnF₂ показана на рис. 5.4.

 

 

VI. ДОМЕННАЯ СТРУКТУРА

 

Ферромагнитные домены

В ферромагнетике при T<T_C все спиновые моменты атомов с недостроенными d- или f-оболочками ориентируются параллельно друг другу. В результате этого намагниченность макроскопического образца должна быть ~ M_s. На опыте же мы знаем, что намагниченность случайно взятого куска ферромагнетика часто» 0. При помещении этого образца в магнитное поле, результирующий магнитный момент возрастает и в достаточно слабых магнитных полях достигает M_s.

 

Гипотезу о существовании областей спонтанной намагниченности - доменов – высказал Вейсс в 1910г. Однако прямое доказательство существования доменов было получено лишь после изобретения способа их наблюдения (метод порошков Битера-1931г., метод коллоидных растворов Акулова -1934г.). В 1935 г. Ландау и Лифшиц дали теоретическое обоснование гипотезы Вейса. Согласно Ландау и Лифшицу макроскопический образец состоит из доменов, намагниченных до насыщения, но ориентированных таким образом, что результирующая намагниченность .

Движение границ при намагничивании, эффект Баркгаузена.

Намагничивание ферромагнитного образца, имеющего М_S = 0 при Н = 0, происходит за счет изменения формы и ориентации доменов. Уже в слабых полях наблюдается увеличение объема "выгодно" расположенных относительно внешнего поля доменов, за счет доменов с "невыгодной" ориентацией, т.е. происходит процесс смещения (движения) границ доменов (рис.6.1а-в). Процесс смещения обратим (при малых Н). Если внешнее поле снять, то домены восстановят исходную форму и размеры. Увеличение поля Н приводит к тому, что рост выгодно ориентированных доменов осуществляется за счет необратимых процессов. Обратимому смещению границ доменов могут, например, препятствовать дефекты кристаллической структуры. Чтобы преодолеть их действие, граница домена должна получить от внешнего поля достаточно большую энергию. Это приводит к эффекту Баркгаузена (1919г.) – скачкообразному изменению намагниченности М при плавном увеличении внешнего поля Н (рис.6.1г). Баркгаузен обнаружил, что при увеличении магнитного поля (или при приближении постоянного магнита к ферромагнетику) возникает шум в громкоговорителе, соединенном с обмоткой вокруг ферромагнетика (рис. 6.2). Если снять намагничивающее поле, то дефекты будут препятствовать возврату границ доменов в исходное положение, обуславливая остаточную намагниченность M_r.

Рис. 6.1. Процессы при намагничивании ферромагнетика: а) Н=0, б) смещение границ доменов, в) вращение вектора намагничивания г) фазы кривой намагничивания, эффект Баркгаузена

Можно выделить следующие фазы в кривой намагничивания (рис.6.1г): I - область линейного намагничивания (обратимого смещения), II - необратимых смещений, III- технического насыщения, когда происходят процессы разворота векторов намагниченностей доменов вдоль поля Н, IV - очень медленный рост намагничивания за счет разворота по полю тех спинов внутри доменов, которые были разупорядочены благодаря конечной температуре. Теория процессов смещения была разработана Кондорским Е.И. (1938г.), а теория вращения Акуловым Н.С.

 

 

Параметры кривой намагничивания

Наиболее важными параметрами кривой намагничения являются: намагниченность и магнитная индукция насыщения - M_s (для единицы объема – I_s), B_s; остаточная (remanence) намагниченность и индукция - M_r (для единицы объема – I_r), B_r; коэрцитивная сила - H_с;

Потери энергии- . (6.1)

Грубо, ферромагнитные материалы разделяются на магнитомягкие материалы (H_c<800A/м»10Э.) и магнитожесткие материалы (H_c>~8000A/м»100 Э).

 

Причины образования доменов. Основные компоненты энергии доменов.

Ландау и Лифшиц показали, что помимо энергии, обусловленной взаимодействием ферромагнетика с внешним магнитным полем (магнитная энергия), необходимо учитывать еще несколько вкладов в энергию, конкуренция которых определяет образование доменной структуры. Рассмотрим энергию некоторой системы доменов в магнитном поле, предполагая, что намагниченность каждого из доменов находится в насыщении. Энергия ферромагнетика записывается как сумма вкладов: 1) магнитной энергии - U_M 2) магнитостатической энергии - U₀, 3) обменной энергии - U_обм, 4) энергии магнитокристаллической анизотропии - U_K, 5) энергия магнитострикционной деформации - U_l, 6) магнитоупругой энергии U_s,

U= U_M +U₀+ U_обм +U_K+U_l+U_s. (6.2)

Минимуму полной энергии ферромагнетика соответствует не насыщенная конфигурация, а некоторая доменная структура.

Охарактеризуем вклады в (6.2).

1) Магнитная энергия - U_M, - это энергия образца во внешнем магнитном поле Н. Согласно (1.13)

U_M= - MH. (6.3)

2) Магнитостатическая энергия - U₀. Появление магнитостатической энергии U₀ связано с тем, что при наличии свободных полюсов возникает размагничивающее поле. Если мы имеем однодоменный кристалл, то сформированные на поверхности этого домена полюса будут иметь большую магнитостатическую энергию порядка (1/8p) ò B² dV ~ M_s²» 10⁶ эрг/см³, где M_s - намагниченность насыщения. Более точно

U₀ = N_PM_s²/2, (6.4)

где N_P - размагничивающий фактор. Магнитостатическая энергия уменьшается, если образец разбивается на антипараллельные намагниченные домены. В частности, для доменов с формой, изображенной на рис. 6.3а,б,в, энергии будут, соответственно, равны [1]:

U_a)~0.85M_S²d; U_б)~0.53M_S²d; U_в)~0.374M_S²d (в системе СГС). (6.5)

Магнитостатическая энергия может быть уменьшена до нуля при образовании доменов, замыкающих магнитные потоки внутри ферромагнитного вещества, как изображено на рис. 6.4.

Рис. 6.3. Некоторые типы магнитных доменов.

Рис. 6.4. Формирование доменной структуры.

При M_S=1.7∙10³ Гс ®U~0.85d3∙10⁶ эрг/см³à0.

 

3) Обменная энергия. Этот вклад определяется выражением

U_обм = - , (6.6)

где J_ij - обменный интеграл. Минимуму U_обм в ферромагнетике соответствует состояние однородной намагниченности со строго параллельной ориентацией магнитных моментов, как показано на рис.6.5а. При этом, однако, неизбежно формируются магнитные полюса, и возрастает вклад магнитостатической энергии U₀. Этот вклад в случае дискообразного образца может быть сведен к нулю при циркулярной ориентации магнитных моментов, как изображено на рис.6.5б – в этом случае полюса отсутствуют. Однако, соседние спины разориентированы на некоторый ненулевой угол, и обменная энергия (6.6) не равна нулю.

 

4) Энергия кристаллической магнитной анизотропии (или магнитокристальная энергия) - U_K. В кристаллах могут быть направления легкого и трудного намагничивания. Например, в оцк a-Fe [100] - направление легкого, а [111] – трудного намагничивания, однако в гцк Ni - ситуация обратная (рис. 6.6). Для гексагонального Со "легкая" ось совпадает с с -осью [0001] (кривая а), а "трудное" направление лежит в базовой плоскости (кривая б).

Причина анизотропии заключена в асимметрии перекрытия электронных орбит (рис.6.7). Вследствие спин-орбитального взаимодействия, распределение заряда - сфероид, а не сфера. Асимметрия в зарядовом распределении обусловлена симметрией кристалла, но также "отслеживает" ориентацию спина за счет L-S-взаимодействия.

Рис.6.7. Асимметрия перекрытия распределений электронов

Рис.6.6. Анизотропия намагничивания в a-Fe, Ni, Co

Вращение направления спина относительно кристаллографических осей изменяет обменную энергию, а также энергию электростатического взаимодействия зарядов в соседних парах атомов. Оба эффекта дают вклад в энергию анизотропии.

Энергия анизотропии в одноосном кристалле может быть представлена в виде ряда

, (6.7)

где a = cos q - направляющий косинус магнитного момента М относительно выделенной оси. Нечетные степени по a не включаются, т.к. направления a и -a эквивалентны, К_n - константы кристаллографической анизотропии не зависят от a и определяются из эксперимента. В большинстве случаев достаточно взять три члена

U_K=K₀+K₁cos²J+K₂cos⁴J. (6.8)

При К₁ <0, K₂ =0 получаем ферромагнетик с легкой осью, поскольку min (U_K) соответствует q=0.

Для кубического кристалла, энергия анизотропии (комбинация a₁² + a₂² +a₃² º1)

U_K=K₀+K₁(a₁²a₂²+a₂²a₃²+a₃²a₁²)+K₂a₁²a₂²a₃². (6.9)

Константы магнитоупругой анизотропии (в эрг/см³) приведены в таблице 6.1:

 

Таблица 6.1. Коэффициенты магнитокристаллической анизотропии для Fe, Ni, Co

Материал	К1, Дж/м3 (эрг/см3)	К2, Дж/м3 (эрг/см3)
Fe	4.6 104 (4.6 105)	-0.075 104 (-0.075 105)
Ni	-5.7 103 (-5.7 104 )	-2.3 103 (-2.3 104)
Co	4.1 105 (4.1 106)	1.0 105 (1.0 106)

Наведенная или ориентационная анизотропия создается искусственно с помощью особой технологии обработки исходного материала, например, при холодной прокатке, отжиге в магнитном поле или в поле внешних упругих напряжений, перекристаллизации в магнитном поле, осаждении пленок в присутствии магнитного поля, осаждении пленок под углом и т.п. Один из механизмов формирования анизотропии - направленное упорядочение дефектов, роль которых могут выполнять атомы замещения и внедрения в сплаве, вакансии, дислокации и т.п. Суть явления - диффузия примесных центров и их упорядочение вдоль таких направлений в кристалле, чтобы возникшая анизотропия стабилизировала имеющуюся ориентацию вектора намагниченности. Например, при отжиге в магнитном поле дефекты упорядочиваются и таким образом образуют одноосную анизотропию с направлением легкой оси, совпадающей с направлением магнитного поля.

Обменная или однонаправленная анизотропия возникает за счет обменных сил на границе двух магнитных фаз: ферромагнетика и антиферромагнетика, см. главу XI.

Поверхностная анизотропия. Поскольку молекулярное поле для ионов в объеме и на поверхности различается, то возникает поверхностная анизотропия, которая важна для тонких пленок. Неель показал, что,

U_{K, пов}=K_пов cos q, (6.10)

где q - угол между вектором спонтанной намагниченности и нормалью к поверхности. Для Fe и Ni U_K,пов ~ 0.1 -1 эрг/см².

 

5) Энергия магнитострикционной деформации -U_l. Магнитострикция - это изменение размеров тела при намагничивании. Так Ni - сжимается в направлении намагничивания и увеличивается в размерах в поперечном направлении, а Fe - в слабых полях увеличивается в направлении намагничивания. Величина D l / l =l_S - константа магнитострикции. Вообще говоря, константа магнитострикции и, соответственно, магнитострикционная деформация, e_ij^M_, являются тензорами:

, (6.11)

где α_k, β_l – напрвляющие косинусы, соответственно, вектора самопроизвольной намагниченности и направления измерения.

В случае кубической симметрии тензор l_ijkl сводится к двум независимым константам l_[100] и l_[111]. В этом случае l можно представить в виде матрицы

(6.12)

Если l_[100]=l_[111]=l, то магнитострикция изотропна, что характерно для полиметаллов. В этом случае можно считать, что

l=(2l_[100]+3l_[111])/5. (6.13)

Для Fe®l_[100]=19.5 10⁶ и l_[111]= - 18.8 10^-6, соответственно, ®l=-3.48 10^-6.

Энергия магнитострикционной деформации

U_l=E_gl_S²/2, (6.14)

где E_l - модуль Юнга. Магнитострикционный эффект является обратимым.

Два соседних домена с противоположными векторами намагниченности [100] и [-100] не обладают упругой энергией, т.к. у них l_S одинаковы (рис. 6.4а), но такая система имеет высокую магнитостатическую энергию за счет формирования свободных полюсов. Энергия ферромагнитного образца понижается при образовании домена в форме трехгранной призмы, замыкающей магнитный поток (рис.6.4б). Замыкающий домен намагничен в направлении, перпендикулярном намагниченности 2-х доменов, т.е. по оси [010]. Поэтому он стремится удлиниться в направлении [010], компенсируя сжатие в этом направлении, обусловленное расширением вдоль [100]. Т.о в замыкающем домене сосредоточен некоторый запас магнитоупругой энергии. Эта энергия пропорциональна объему замыкающего домена. Если остальные факторы не препятствуют, то образуется такое число доменов, при котором достигается минимум суммы энергий основных и замыкающих доменов (рис.6.4в).

 

6) Магнитоупругая энергия - U_s. Магнитострикция - частный случай магнитоупругих взаимодействий. При наличии внешнего напряжения s_ij возникает деформация e_ij^M. Соответственно, эта энергия равна

U_s = -ås_ij e_ij^M. (6.15)

 

 

Границы доменов

Стенки Блоха.

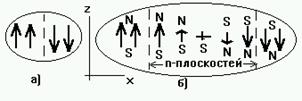Рис. 6.8. Стенки Блоха.

Домены отделены друг от друга границами, в которых осуществляется изменение ориентации спина. Если при развороте вектор намагничивания не выходит из плоскости yz (см. рис 6.8а), то эти границы называют стенками Блоха. На рис. 6.8а поворот спинов на 180⁰ происходит скачком, т.е. в одной плоскости. Для этого требуется энергия:

DE=-JS(-S) - [-JS²] = 2JS² (6.16)

Во втором случае (рис. 6.8б) поворот происходит в стенке, состоящей из n-плоскостей, в каждой из которых спин поворачивается на угол p/n. Тогда обменная энергия между соседними спинами равна DE = -Js²cos(p/n), а полная энергия равна

DE_обм = n[-JS²cos(p/n)-(-JS²)] = nJS²[1-cos(p/n)]. (6.17)

При n>>1 получаем

DE» JS²p²/n. (6.18)

Согласно (6.18) толщина стенки могла бы расти бесконечно, но этому препятствует энергия анизотропии: спин в стенке Блоха не ориентирован в направлении легкого намагничивания. Поэтому, доля энергии анизотропии DE_K ~ n. Баланс между обменной энергией и энергией анизотропии достигается в Fe на толщине ~ 150a (а-период решетки):

W_wall» p² JS² /na² + Kna, (6.19)

где K – константа анизотропии.

Оценки показывают, что полная энергия стенки составляет W_wall ~1 erg/cm².

Толщина стенкиБлоха может быть определена из условия ¶W/¶n = -p²JS²/2n²a²+Ka = 0. Отсюда,

n = (p²JS²/2Ka³)^1/2, (6.20)

и, соответственно, толщина

d = na = (p²JS²/Ka)^1/2 = p(A/K)^1/2 = pd₀, (6.21)

где A = JS²/a - (6.21а)

плотность обменной энергии, а плотность энергии границы -

s=2p(JKS²/a)^1/2=2p(AK)^1/2=2ps₀. (6.21б)

Итак, в массивных ферромагнетиках магнитостатическая энергия (энергия свободных полюсов) отсутствовала в объеме, а на поверхности пренебрегалась из-за малости отношения (площадь поверхности)/(объем) ® 0. В тонких пленках поверхностью пренебрегать можно не всегда. Впервые на значение магнитостатической энергии в тонких пленках указал Неель.

Неелевские границы.

Рис. 6.9 Блоховские (а) и неелевские (б) границы.

Неель, в частности, показал, что поворот вектора М может происходить в плоскости пленки, даже если векторы намагничивания лежат в плоскости пленки (рис.6.9). При каких условиях неелевские стенки становятся более выгодными, чем блоховские? Блоховские границы выгоднее, когда мал вклад магнитостатической энергии. В тонких пленках отношение площади поверхности к объему для доменов перестает быть пренебрежимо малым, поэтому вклад магнитостатической энергии в блоховской границе возрастает. Аппроксимируя границу цилиндром эллиптического сечения, для магнитостатической энергии получаем

U₀=N_PM_эфф²/2 (6.22)

где M_эфф - эффективная (средняя) намагниченность, изображенная вектором в стенке на рис. 6.9. Размагничивающий фактор в таком приближении будет равен

для стенки Блоха

N_P^Bl =4pd/(d+h), (6.23а)

для стенки Нееля

N_P^Neel=4ph/(h+d), (6.23б)

где h толщина пленки. В обоих случаях M_эфф² примерно совпадают и равны M_эфф»M_s/Ö2, поэтому вклад магнитостатической энергии стенок в поверхностную плотность энергии s₀ = U₀d равен

s₀^Bl=pd²/(h+d) M_s², (6.24а)

s₀^Neel=phd/(h+d) M_s². (6.24б)

Из сопоставления этих выражений мы видим, что при h<d плотность энергии неелевской границы меньше блоховской. Эксперимент показывает, что в пленках Fe, Ni, пермаллоя неелевские границы появляются при h<100 нм.

Справка: Пермаллой = perm(eabiliti)+alloy - общее название группы сплавов Ni-Fe+Cu/Cr/Mo/Mn. Обладает большой c. Сендаст (sendust -Fe+9.5%Si+5.5%Al) также обладает высокой магнитной восприимчивостью.

На рис.6.10 представлены зависимости плотности энергии доменных стенок от толщины пленки пермаллоя, рассчитанные в работах [2, 3, 4]. Согласно этим расчетам, неелевская граница становится выгодной только при толщинах менее 80 нм. Причиной перехода от стенок Блоха к стенке Нееля является уменьшение вкладов обменной энергии и энергии намагничения, по сравнению с энергией размагничения, как это видно из рис. 6.11. Вклад энергии анизотропии в данном диапазоне толщин, как видно из рисунка, мал.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: