 |
Связь линейных и угловых величин в кинематике.
|
|
|
|
План занятий.
1. Разбор вопросов студентов по домашнему заданию.
2. Решение типовых задач на доске.
3. Самостоятельное решение студентами некоторых задач на занятии и подведение итогов.
4. Формулировка домашнего задания.
Темы занятий.
1. Кинематика поступательного и вращательного движения. Тангенциальное и нормальное ускорение, радиус кривизны.
2. Динамика поступательного и вращательного движения.
3. Законы сохранения импульса, момента импульса и механической энергии
4. Контрольная работа из 4 задач по темам, рассмотренным на первых трех занятиях.
5. Механические колебания: собственные незатухающие и затухаюшие, вынужденные.
6. Идеальный газ: уравнение состояния, работа, внутренняя энергия, теплоемкость. Первое начало термодинамики.
7. Второе начало термодинамики. КПД тепловой машины. Распределения Максвелла и Больцмана.
8. Контрольная работа из 4 задач по темам, рассмотренным на 5-7 занятиях.
Занятие 1.
Кинематика поступательного и вращательного движения.
Тангенциальное и нормальное ускорение, радиус кривизны.
Положение частицы в пространстве определяется радиус-вектором 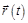 , который начинается в начале системы координат и заканчивается на частице.
, который начинается в начале системы координат и заканчивается на частице.
Скорость частицы 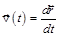 (перемещение за единицу времени). Кроме понятия скорости часто используют понятие средней скорости
(перемещение за единицу времени). Кроме понятия скорости часто используют понятие средней скорости 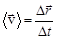 .
.
Ускорение частицы 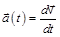 (изменение скорости за единицу времени)
(изменение скорости за единицу времени)
Для решения кинематических задач поступательного движения удобно пользоваться декартовой системой координат, в которой любой вектор можно разложить на три проекции вдоль осей х, y и z:
Радиус-вектор 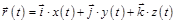 . (1.1,а)
. (1.1,а)
Скорость частицы 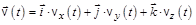 . (1.1,б)
. (1.1,б)
Ускорение частицы 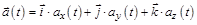 . (1.1,в)
. (1.1,в)
|
|
|
Здесь  – единичные векторы (орты), направленные по осям
– единичные векторы (орты), направленные по осям 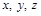 соответственно.
соответственно.
Прямая задача кинематики
Если известны зависимости  , то можно определить проекции скорости и ускорения на оси
, то можно определить проекции скорости и ускорения на оси 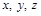 ,:
,:
 (1.2,а)
(1.2,а)
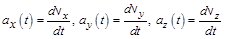 (1.2,б)
(1.2,б)
Величины (модули) векторов можно найти, используя теорему Пифагора: 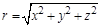 ;
; 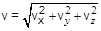 ;
; 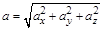 . (1.3)
. (1.3)
Обратная задача кинематики
Если известны зависимости 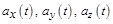 и начальные условия
и начальные условия  ,
,  ,
, 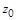 ,
, 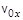 ,
,  ,
, 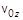 , то можно определить проекции скорости, а затем и координаты частицы в любой момент времени, т.е. определить закон ее движения:
, то можно определить проекции скорости, а затем и координаты частицы в любой момент времени, т.е. определить закон ее движения:
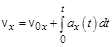 ;
; 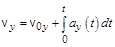 ;
; 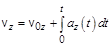 (1.4,а)
(1.4,а)
 ;
;  ;
; 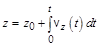 (1.4,б)
(1.4,б)
Величина перемещения частицы
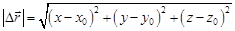 (1.4,в)
(1.4,в)
есть кратчайшее расстояние между начальным и конечным положением частицы в пространстве. Если движение частицы происходит не по прямой линии, то длина траектории, называемая путем, больше перемещения 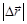 . Путь, пройденный частицей за время t:
. Путь, пройденный частицей за время t:
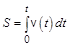 (1.5)
(1.5)
Кинематика вращательного движения.
Если твердое тело вращается вокруг закрепленной оси z и известна зависимость угла поворота 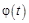 , то можно рассчитать проекции на ось вращения его угловой скорости
, то можно рассчитать проекции на ось вращения его угловой скорости 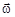 и углового ускорения
и углового ускорения  :
:

 . (1.6)
. (1.6)
Если известна зависимость  и начальные условия
и начальные условия  и
и 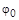 , то можно найти проекцию
, то можно найти проекцию 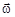 и угол поворота в зависимости от времени:
и угол поворота в зависимости от времени:
 и
и 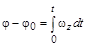 (1.7)
(1.7)
Связь линейных и угловых величин в кинематике.
При криволинейном движении ускорение частицы имеет тангенциальную 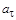 и нормальную
и нормальную 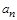 составляющие, причем
составляющие, причем
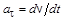 ,
,  , (1.8)
, (1.8)
где R – радиус кривизны траектории. Полное ускорение
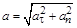 . (1.9)
. (1.9)
Линейные и угловые величины связаны следующим образом:
 ;
; 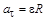 ;
;  (1.10)
(1.10)
1.1. Радиус-вектор частицы зависит от времени по закону:
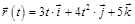 . Найдите тангенс угла между вектором скорости
. Найдите тангенс угла между вектором скорости 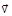 и осью х в момент времени
и осью х в момент времени  2 с.
2 с.
1.2. Частица начала свое движение из начала координат с начальной скоростью  м/с, и с ускорением, которое зависит от времени по закону
м/с, и с ускорением, которое зависит от времени по закону 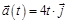 м/с2. Каков модуль скорости частицы в момент времени
м/с2. Каков модуль скорости частицы в момент времени 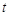 = 3 с.
= 3 с.
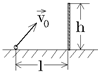 1.3. Маленькая лягушка находится на расстоянии l = 1 м от стенки и прыгает с начальной скоростью v 0 = 4 м/с. Стенку какой наибольшей высоты может перепрыгнуть лягушка? Принять g = 10 м/с 2.
1.3. Маленькая лягушка находится на расстоянии l = 1 м от стенки и прыгает с начальной скоростью v 0 = 4 м/с. Стенку какой наибольшей высоты может перепрыгнуть лягушка? Принять g = 10 м/с 2.
|
|
|
Ответ: 
1.4. Колесо начинает вращаться вокруг своей оси с угловым ускорением 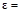 4 рад / c 2. Через какой промежуток времени угол между вектором скорости и вектором ускорения точки на ободе колеса станет равным
4 рад / c 2. Через какой промежуток времени угол между вектором скорости и вектором ускорения точки на ободе колеса станет равным 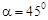 ?
?  Ответ:
Ответ: 
1.5. Кузнечик прыгает с некоторой начальной скоростью под углом 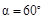 к горизонту. Определить радиус кривизны его траектории сразу после прыжка, если в верхней точке траектория имеет радиус кривизны R = 40 см. Ответ:
к горизонту. Определить радиус кривизны его траектории сразу после прыжка, если в верхней точке траектория имеет радиус кривизны R = 40 см. Ответ: 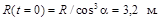
Качественные задачи.
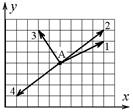 1.6к. Радиус-вектор частицы изменяется во времени по закону
1.6к. Радиус-вектор частицы изменяется во времени по закону 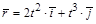 .
.
В момент времени t = 1 с частица оказалась в некоторой точке А. Выберите правильное направление скорости частицы в этот момент времени. а) 1; б) 2; в) 3; г) 4;
д) на рисунке нет правильного направления
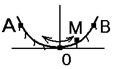 1.7к. Материальная точка M свободно без трения скользит в поле силы тяжести по гладким стенкам симметричной ямы (A и B – наивысшие точки подъема). При этом величина тангенциальной (касательной к траектории) проекции ускорения точки М:
1.7к. Материальная точка M свободно без трения скользит в поле силы тяжести по гладким стенкам симметричной ямы (A и B – наивысшие точки подъема). При этом величина тангенциальной (касательной к траектории) проекции ускорения точки М:
а) отлична от нуля в точке В;
б) максимальна в нижней точке траектории О;
в) равна нулю в точке А; г) одинакова во всех точках траектории;
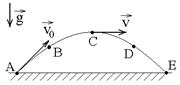 1.8к. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль тангенциального ускорения
1.8к. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль тангенциального ускорения 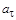 на участке А-В-С:
на участке А-В-С:
1) уменьшается 2) увеличивается 3) не изменяется
1.9к. Тело брошено с поверхности Земли со скоростью 10 м/с под углом 45° к горизонту. Если сопротивлением воздуха пренебречь и принять g = 10 м/с2, то радиус кривизны траектории в верхней точке (в метрах) равен.....
 1.10к. Из-за неисправности мотора величина скорости автомобиля синусоидально изменялась во времени, как показано на графике зависимости V(t). В момент времени t1 автомобиль поднимался по участку дуги. Куда может быть направлена результирующая всех сил, действующих на автомобиль в этот момент времени?
1.10к. Из-за неисправности мотора величина скорости автомобиля синусоидально изменялась во времени, как показано на графике зависимости V(t). В момент времени t1 автомобиль поднимался по участку дуги. Куда может быть направлена результирующая всех сил, действующих на автомобиль в этот момент времени?
1) 1 2) 2 3) 3 4) 4 5) 5
 1.11к. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. На каких участках графика зависимости
1.11к. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. На каких участках графика зависимости 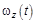 вектор угловой скорости
вектор угловой скорости  и вектор углового ускорения
и вектор углового ускорения 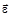 направлены в одну сторону? 1) 0 - А и А-В 2) 0 -А и В - С 3) В - С и С - D
направлены в одну сторону? 1) 0 - А и А-В 2) 0 -А и В - С 3) В - С и С - D
|
|
|
4) всегда направлены в одну сторону
 1.12к. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. В какой момент времени угол поворота тела относительно начального положения будет максимальным?
1.12к. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. В какой момент времени угол поворота тела относительно начального положения будет максимальным?
а) 10 с б) 1 с в) 2 с г) 9 с
 1.13к. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике. Во сколько раз отличаются величины тангенциальных ускорений точки на краю диска в моменты времени t 1 = 2 с и t 2 =7 с?
1.13к. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике. Во сколько раз отличаются величины тангенциальных ускорений точки на краю диска в моменты времени t 1 = 2 с и t 2 =7 с?
а) в 2 раза б) в 4 раза в) оба равны нулю г) трудно определить точно
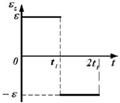 1.14к. Твердое тело начинает вращаться вокруг оси Z. Зависимость углового ускорения
1.14к. Твердое тело начинает вращаться вокруг оси Z. Зависимость углового ускорения 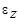 от времени представлена на графике. Соответствующая зависимость угловой скорости
от времени представлена на графике. Соответствующая зависимость угловой скорости 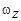 от времени представлена графиком...
от времени представлена графиком...
а) 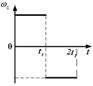 б)
б) 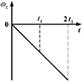 в)
в)  г)
г) 
1.15к. Прямолинейное движение точки описывается уравнением 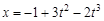 (в единицах СИ). Средняя скорость точки за время движения до остановки в м/с равна....
(в единицах СИ). Средняя скорость точки за время движения до остановки в м/с равна....
|
|
|


