 |
Собственные незатухающие и затухаюшие, вынужденные.
|
|
|
|
Если на тело действует сила, пропорциональная смещению тела из положения равновесия и направленная в противоположную смещению сторону, то тело будет колебаться по гармоническому закону:
 (4.1)
(4.1)
где 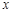 – смещение из положения равновесия,
– смещение из положения равновесия, 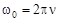 – циклическая частота колебаний,
– циклическая частота колебаний,  – частота, а
– частота, а 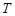 – период колебаний,
– период колебаний, 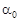 – начальная фаза колебаний,
– начальная фаза колебаний,  – амплитуда или максимальное смещение. Примером такого движения является колебания тела на пружине вдоль некорой оси
– амплитуда или максимальное смещение. Примером такого движения является колебания тела на пружине вдоль некорой оси 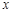 , начало отсчета которой находится в положении равновесия. Такое движение удовлетворяет условию гармонических колебаний, так как проекция силы упругости равна
, начало отсчета которой находится в положении равновесия. Такое движение удовлетворяет условию гармонических колебаний, так как проекция силы упругости равна  , где
, где  – коэффициент жесткости пружины. Такое тело массы
– коэффициент жесткости пружины. Такое тело массы  на пружине с жесткостью
на пружине с жесткостью  называется пружинным маятником. Циклическую частоту и период его колебаний определяют по формулам:
называется пружинным маятником. Циклическую частоту и период его колебаний определяют по формулам:
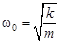 ,
,  (4.2)
(4.2)
Если на тело, способное вращаться вокруг некоторой закрепленной оси, действует момент силы, пропорциональный углу отклонения j от положения равновесия и стремящийся вернуть тело в положение равновесия, то угол отклонения j будет меняться по гармоническому закону (только в случае малости угла, т.е. если 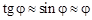 рад:)
рад:)
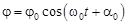 , (4.3)
, (4.3)
 где
где 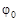 – угловая амплитуда колебаний или максимальный угол отклонения от положения равновесия. Примером таких колебаний может служить физический маятник, то есть любое твердое тело, колеблющееся вокруг закрепленной оси О, лежащей выше центра масс С этого тела, под действием момента силы тяжести. В случае горизонтальной оси О циклическая частота и период колебаний физического маятника определяются по формулам:
– угловая амплитуда колебаний или максимальный угол отклонения от положения равновесия. Примером таких колебаний может служить физический маятник, то есть любое твердое тело, колеблющееся вокруг закрепленной оси О, лежащей выше центра масс С этого тела, под действием момента силы тяжести. В случае горизонтальной оси О циклическая частота и период колебаний физического маятника определяются по формулам:
 ,
,  , (4.4)
, (4.4)
где g – ускорение свободного падения, d= OC – расстояние от центра масс до оси вращения, I – момент инерции твердого тела относительно оси вращения (см. (2.5) – (2.7)).
|
|
|
Для системы твердых тел, совершающих колебание как единое целое, при расчете циклической частоты (4.4) необходимо учесть, что 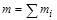 ,
, 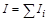 , где
, где 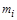 и
и  – массы и моменты инерции каждого тела в отдельности. Также необходимо рассчитать расстояние d от центра масс СИСТЕМЫ ТЕЛ до оси вращения.
– массы и моменты инерции каждого тела в отдельности. Также необходимо рассчитать расстояние d от центра масс СИСТЕМЫ ТЕЛ до оси вращения.
Частный случай физического маятника – математический маятник – подвешенное на невесомой нерастяжимой нити тело, рамеры которого намного меньше длины нити 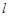 . Циклическая частота и период колебаний такого маятника определяется по формулам:
. Циклическая частота и период колебаний такого маятника определяется по формулам:
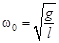 ,
,  (4.5)
(4.5)
Из (4.1) можно найти скорость тела на пружине в любой момент времени: 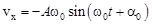 , (4.6)
, (4.6)
где 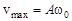 – амплитуда скорости (максимальная скорость).
– амплитуда скорости (максимальная скорость).
Их (4.3) можно найти угловую скорость вращения физического или математического маятника:
 (4.7)
(4.7)
где 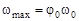 – максимальная угловая скорость вращения.
– максимальная угловая скорость вращения.
Если маятник любого типа находится в вязкой среде, то колебания такого маятника будут затухающими (или вообще могут не возникнуть), т.е. назвать их гармоническими уже нельзя. Кинематическое уравнение колебаний для пружинного маятника (4.1) изменяется:
 , (4.8)
, (4.8)
где  (4.9)
(4.9)
– амплитуда затухающих колебаний, уменьшающаяся со временем по экспоненциальному закону (не путать с максимальным отклонением от положения равновесия!), 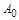 – начальная амплитуда колебаний (не путать с начальным смещением из положения равновесия!),
– начальная амплитуда колебаний (не путать с начальным смещением из положения равновесия!),
Коэффициент затухания характеризует скорость уменьшения амплитуды  , (4.10)
, (4.10)
где t – время релаксации, или время, за которое амплитуда уменьшится в е раз, где е = 2,72 – основание натурального логарифма).
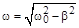 (4.11)
(4.11)
– циклическая частота затухающих колебаний, где 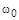 – циклическая частота колебаний в отсутствие вязкой среды (без диссипативных сил). Видно, что если
– циклическая частота колебаний в отсутствие вязкой среды (без диссипативных сил). Видно, что если 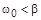 , то действительного значения для w не существует, т.е. колебания не возникают (слишком вязкая среда, например, мед или дёготь).
, то действительного значения для w не существует, т.е. колебания не возникают (слишком вязкая среда, например, мед или дёготь).
Период затухающих колебаний 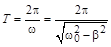 .
.
|
|
|
Логарифмический декремент затухания
 (4.12)
(4.12)
характеризует уменьшение амплитуды колебаний за один период.
Все вышесказанное относится к математическому и физическому маятникам, кроме переменной – вместо смещения х надо рассматривать угловое смещение j:
 (4.13)
(4.13)
Если к пружинному маятнику вдоль оси колебаний приложить внешнюю гармоническую силу  , то маятник будет совершать вынужденные колебания с частотой вынуждающей силы
, то маятник будет совершать вынужденные колебания с частотой вынуждающей силы  по закону:
по закону: 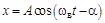 ,
,
где 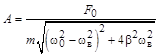 (4.14)
(4.14)
– амплитуда вынужденных колебаний.
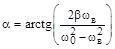 (4.15)
(4.15)
– отставание по фазе смещения от внешней силы.
Если затухание колебаний мало 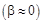 , то выражение для амплитуды упростится:
, то выражение для амплитуды упростится:  , a = 0.
, a = 0.
 4.1. Два одинаковых диска массы m = 1 кги радиуса R =1 м положили на одну плоскость и приварили в одной точке. Затем получившуюся фигуру подвесили на горизонтальной оси, перпендикулярной плоскости фигуры и проходящей через точку О. Точка О и центры масс двух дисков лежат на одной прямой. Трением в оси пренебречь. Найдите период малых колебаний фигуры вокруг точки О. Ответ: 3,29 c
4.1. Два одинаковых диска массы m = 1 кги радиуса R =1 м положили на одну плоскость и приварили в одной точке. Затем получившуюся фигуру подвесили на горизонтальной оси, перпендикулярной плоскости фигуры и проходящей через точку О. Точка О и центры масс двух дисков лежат на одной прямой. Трением в оси пренебречь. Найдите период малых колебаний фигуры вокруг точки О. Ответ: 3,29 c
4.2. Грузик массой m = 1 кгприкреплен к пружине жесткости k = 1 Н/ми совершает незатухающие гармонические колебания в горизонтальной плоскости с амплитудой A = 1 см. В начальный момент грузик вышел из положения равновесия. За какое время он пройдет путь, равный 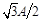 ? Ответ: 1,05 с
? Ответ: 1,05 с
4.3. Маленький шарик подвешен на длинной нерастяжимой нити длины l = 1 м и совершает гармонические колебания под действием силы тяжести. В нижней точке траектории шарик имеет угловую скорость w = 2 рад/с. Найдите максимальный угол (в радианах), на который отклоняется нить в процессе движения. g = 10 м/с2. Ответ: 0,63 рад
4.4. Пружинный маятник совершает малые вертикальные колебания по закону  . Найти массу маятника, если коэффициент жёсткости пружины k = 1 H/м. Ответ: m = 40 г.
. Найти массу маятника, если коэффициент жёсткости пружины k = 1 H/м. Ответ: m = 40 г.
4.5. Однородный тонкий диск радиуса R осциллирует около закреплённой горизонтальной оси, проходящей перпендикулярно плоскости диска через его край. Вследствие трения его колебания затухают. Найти период таких колебаний, если логарифмический декремент затухания колебаний равен 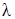 . Ответ:
. Ответ:  .
.
 4.6. Грузик массы m совершает вертикальные колебания на пружинке с коэффициентом жёсткости k = 6 H / м под действием внешней гармонической силы с амплитудой F 0 = 0,1 Н. Найти частоту этой силы, если амплитуда колебаний грузика А = 2 см. Трением пренебречь. Ответ:
4.6. Грузик массы m совершает вертикальные колебания на пружинке с коэффициентом жёсткости k = 6 H / м под действием внешней гармонической силы с амплитудой F 0 = 0,1 Н. Найти частоту этой силы, если амплитуда колебаний грузика А = 2 см. Трением пренебречь. Ответ: 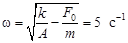 .
.
|
|
|
|
|
|


