 |
Распределения Максвелла и Больцмана.
|
|
|
|
Изучая процесс превращения теплоты в работу, Р.Клаузиус в 1865 г ввел понятие энтропии 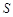 , которое определил через ее приращение
, которое определил через ее приращение  :
:
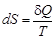 , (6.1)
, (6.1)
где 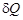 – бесконечно малое приращение тепла, полученное термодинамической системой при данной температуре.
– бесконечно малое приращение тепла, полученное термодинамической системой при данной температуре.
Энтропия – функция состояния системы. Если известен явный вид зависимости энтропии от термодинамических параметров (температуры, давления, объема), то из (6.1) можно рассчитать количество тепла, полученное системой в заданном процессе:
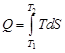 (6.2)
(6.2)
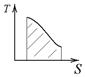
Если дана зависимость температуры от энтропии в виде графика, то теплота, полученная газом определяется, как площадь под кривой  (см. рис.).
(см. рис.).
Теормодинамическую систему, совершающую циклический процесс и совершающую работу за счет получения тепла от нагревателя, называют тепловой машиной. Характерным параметром тепловой машины является коэффициент полезного действия:
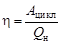 или
или 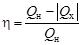 . (6.3)
. (6.3)
где  – работа, совершенная машиной за цикл. Чтобы тепловая машина могла работать непрерывно, она должна совершать циклический процесс, получая некоторую порцию тепла от нагревателя
– работа, совершенная машиной за цикл. Чтобы тепловая машина могла работать непрерывно, она должна совершать циклический процесс, получая некоторую порцию тепла от нагревателя 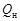 и обязательно отдать часть тепла холодильнику
и обязательно отдать часть тепла холодильнику  . Нагревателем и холодильником могут служить более нагретое тело с температурой
. Нагревателем и холодильником могут служить более нагретое тело с температурой 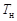 (печь) и менее нагретое с температурой
(печь) и менее нагретое с температурой 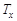 (холодная вода), с которыми по очереди контактирует рабочее тело (например газ в цилиндре под поршнем).
(холодная вода), с которыми по очереди контактирует рабочее тело (например газ в цилиндре под поршнем).
Самый большой КПД при одинаковых 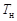 и
и 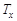 будет у тепловой машины, работающей по циклу Карно, состоящего из двух изотерм и двух адиабат. Такую машину называют идеальной тепловой машиной и ее КПД
будет у тепловой машины, работающей по циклу Карно, состоящего из двух изотерм и двух адиабат. Такую машину называют идеальной тепловой машиной и ее КПД
 (6.4)
(6.4)
 Если рабочий цикл тепловой машины изображен графически в виде замкнутой фигуры в координатах
Если рабочий цикл тепловой машины изображен графически в виде замкнутой фигуры в координатах  , то работа газа за цикл будет равна площади этой фигуры (см. рис. цикл 1-2-3-1). Тепло, полученное от нагревателя, находится при этом как площадь под кривой 1-2, где энтропия возрастает (на участке 2-3 тепло отдается холодильнику).
, то работа газа за цикл будет равна площади этой фигуры (см. рис. цикл 1-2-3-1). Тепло, полученное от нагревателя, находится при этом как площадь под кривой 1-2, где энтропия возрастает (на участке 2-3 тепло отдается холодильнику).
|
|
|
Продолжателем идей Р.Клаузиуса в молекулярно-кинетической теории газов, в которую тот ввел элементы теории вероятности, был Д.К.Максвелл, получивший функцию распределения молекул идеального газа по модулям их скоростей  :
:
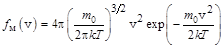 , (6.5)
, (6.5)
где 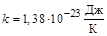 – постоянная Больцмана;
– постоянная Больцмана; 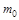 – масса одной молекулы. С помощью этой функции можно рассчитать относительную долю молекул, обладающих скоростями в диапазоне от
– масса одной молекулы. С помощью этой функции можно рассчитать относительную долю молекул, обладающих скоростями в диапазоне от 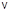 до
до  .
.
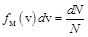 . (6.6)
. (6.6)
Интегрируя выражение (6.6), можно убедиться, что относительная доля молекул, обладающих скоростями в бесконечном диапазоне скоростей, равна 1:  (6.7)
(6.7)
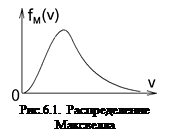 На рис.6.1 показан вид функции распределения Максвелла, имеющий максимальное значение при некоторой скорости, которая называется средней вероятной скоростью:
На рис.6.1 показан вид функции распределения Максвелла, имеющий максимальное значение при некоторой скорости, которая называется средней вероятной скоростью:
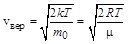 , (6.8)
, (6.8)
где 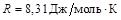 – универсальная газовая постоянная; m – молярная масса газа.
– универсальная газовая постоянная; m – молярная масса газа.
Анализируя формулы (6.8) и (6.7) можно прийти к выводу, что при увеличении температуры положение максимума функции распределения смещается вправо по оси скоростей, но при этом площадь под кривой не меняется и равна всегда 1.
Кроме средней вероятной скорости (6.8) в молекулярно-кинетической теории используется понятие средней скорости
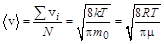 (6.9)
(6.9)
и среднеквадратичной скорости
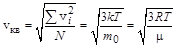 . (6.10)
. (6.10)
Используя распределение Максвелла по проекциям скоростей, можно найти число ударов молекул  в единицу времени
в единицу времени 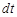 (частоту ударов) о поверхность единичной площади
(частоту ударов) о поверхность единичной площади 
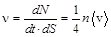 (6.11)
(6.11)
и среднюю длину свободного пробега молекулы
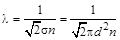 , (6.12)
, (6.12)
где  – концентрация молекул газа,
– концентрация молекул газа, 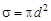 – эффективное сечение молекулы,
– эффективное сечение молекулы, 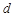 – эффективный диаметр молекулы.
– эффективный диаметр молекулы.
Кроме распределения Максвелла по скоростям молекул (6.5) необходимо упомянуть распределение Больцмана по высоте молекул в равновесном изотермическом столбе газа (например в изотермической модели атмосферы):  , (6.13)
, (6.13)
|
|
|
где 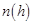 и
и 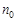 – концентрации молекул газа на высоте
– концентрации молекул газа на высоте  от поверхности Земли и на нулевой высоте соответственно, m – молярная масса газа,
от поверхности Земли и на нулевой высоте соответственно, m – молярная масса газа, 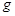 – ускорение свободного падения, которое считается постоянным в пределах всего столба газа,
– ускорение свободного падения, которое считается постоянным в пределах всего столба газа, 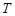 – абсолютная температура, постоянная по всему столбу газа.
– абсолютная температура, постоянная по всему столбу газа.
Формула для давления газа
 (6.14)
(6.14)
в сочетании с (6.13) позволяет определить давление газа на разных высотах в изотермической равновесной атмосфере или барометрическую формулу: 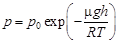 (6.15)
(6.15)
Необходимо учесть тот факт, что давление атмосферы около поверхности Земли не зависит от температуры, так как масса всего воздуха в атмосфере, который своим весом давит на площадь Земли, не меняется ни зимой, ни летом.
6.1. Два моля азота сначала изобарически нагревают в два раза, а затем изотермически сжимают в два раза. Найти суммарное изменение энтропии в этих двух процессах. Ответ: 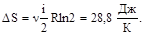
6.2. Теплоёмкость термодинамической системы (не идеального газа) в некотором процессе изменяется с температурой по закону C = b/T2, где b = 800 кДж . К. Найти изменение энтропии системы в этом процессе при её нагревании от T 1 = 100 K до T 2 = 200 K.
Ответ: 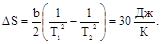
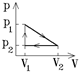 6.3. Идеальный трёхатомный газ совершает циклический процесс, изображённый на диаграмме, где p 1 = 3p 2, V 2 = 5V 1. Найти к.п.д. этого процесса.
6.3. Идеальный трёхатомный газ совершает циклический процесс, изображённый на диаграмме, где p 1 = 3p 2, V 2 = 5V 1. Найти к.п.д. этого процесса.
Ответ: 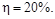
6.4. К.п.д. циклического процесса, изображённого на T – S – диаграмме, равен  Найти температуру T1, если T3 = 300 К, а T 2 = 350 К.
Найти температуру T1, если T3 = 300 К, а T 2 = 350 К.
 Ответ: T1 = 400 K.
Ответ: T1 = 400 K.
6.5. Идеальный газ находился в закрытом сосуде, а средняя квадратичная скорость молекул была равна  . Потом газ был нагрет так, что средняя вероятная скорость молекул стала равна
. Потом газ был нагрет так, что средняя вероятная скорость молекул стала равна  .
.  =500 м/с;
=500 м/с;  =450 м/с. Найти: отношение частоты ударов молекул о единичную площадку в первом и во втором состояниях
=450 м/с. Найти: отношение частоты ударов молекул о единичную площадку в первом и во втором состояниях 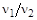 .
.
Качественные задачи
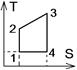 6.7к. На рисунке представлен прямой цикл тепловой машины в координатах
6.7к. На рисунке представлен прямой цикл тепловой машины в координатах  , где
, где 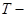 термодинамическая температура,
термодинамическая температура, 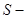 энтропия. Укажите участки, на которых тепло поступает в рабочее тело машины от нагревателей, и участки, где тепло отдается холодильнику:
энтропия. Укажите участки, на которых тепло поступает в рабочее тело машины от нагревателей, и участки, где тепло отдается холодильнику:
а) 12, 23 – поступает; 41 – отдается б) 23 – поступает; 41 – отдается
в) 12, 23 – поступает; 34, 41 – отдается г) 12 – поступает; 34 – отдается
 6.8к. Идеальная тепловая машина работает по циклу Карно (две изотермы 1-2 и 3-4 и две адиабаты 2-3 и 4-1). Как изменится энтропия рабочего тела в процессе изотермического расширения 1-2?
6.8к. Идеальная тепловая машина работает по циклу Карно (две изотермы 1-2 и 3-4 и две адиабаты 2-3 и 4-1). Как изменится энтропия рабочего тела в процессе изотермического расширения 1-2?
|
|
|
1) энтропия возрастет
2) энтропия уменьшится 3) энтропия не изменится
 6.9к. На рисунке представлен график распределения молекул идеального газа по величинам скоростей (распределение Максвелла). С ростом температуры
6.9к. На рисунке представлен график распределения молекул идеального газа по величинам скоростей (распределение Максвелла). С ростом температуры 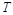 газа площадь под этим графиком будет:
газа площадь под этим графиком будет:
а) оставаться неизменной б) расти пропорционально 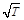
в) расти пропорционально 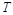 г) расти пропорционально
г) расти пропорционально 
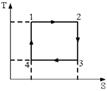 6.10к. На рисунке изображен цикл Карно в координатах (Т, S), где S – энтропия. Адиабатное расширение происходит на этапе...
6.10к. На рисунке изображен цикл Карно в координатах (Т, S), где S – энтропия. Адиабатное расширение происходит на этапе...
а) 3 – 4 б) 4 – 1 в) 2 – 3 г) 1 – 2
6.11к. Если количество теплоты, отдаваемое рабочим телом холодильнику, увеличится в два раза, то коэффициент полезного действия тепловой машины...
а) уменьшится на 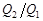 ; б) увеличится на
; б) увеличится на 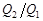 ;
;
в) увеличится на  ; г) уменьшится на
; г) уменьшится на 
6.12к. Зависимость концентрации молекул идеального газа во внешнем однородном поле силы тяжести от высоты для двух разных температур  представлена на рисунке...
представлена на рисунке...
а) 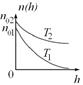 б)
б)  в)
в) 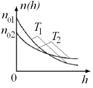 г)
г) 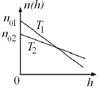
6.12к. Зависимость давления идеального газа во внешнем однородном поле силы тяжести от высоты для двух разных температур  представлена на рисунке...
представлена на рисунке...
а)  б)
б) 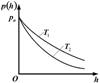 в)
в)  г)
г) 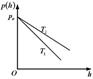
|
|
|


