 |
Идеальный газ: уравнение состояния, работа, внутренняя энергия, теплоемкость. Первое начало термодинамики.
|
|
|
|
Идеальный газ это модель, в которой принимаются следующие упрощения:
1) суммарным объемом всех молекул можно пренебречь по сравнению с объемом сосуда;
2) молекулы взаимодействуют только при соударениях друг с другом и со стеной сосуда, но взаимодействием молекул на расстоянии можно пренебречь.
Уравнение состояния идеального газа (Менделеева-Клапейрона) связывает три макропараметра термодинамической системы (газа) – давление 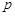 , объем
, объем  и абсолютную температуру
и абсолютную температуру 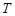 , измеряемую в Кельвинах:
, измеряемую в Кельвинах:  , (5.1)
, (5.1)
где  – количество вещества или число молей,
– количество вещества или число молей,  – масса газа в сосуде,
– масса газа в сосуде,  – молярная масса газа.
– молярная масса газа.
Абсолютная температура является мерой средней кинетической энергии молекулы:  (5.2)
(5.2)
где  =
=  – число степеней свободы молекулы газа или число независимых координат, с помощью которых можно описать положение молекулы в пространстве, причем
– число степеней свободы молекулы газа или число независимых координат, с помощью которых можно описать положение молекулы в пространстве, причем 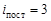 – число поступательных степеней свободы,
– число поступательных степеней свободы,  – число вращательных степеней свободы,
– число вращательных степеней свободы,  – число колебательных степеней свободы,
– число колебательных степеней свободы,  Дж/К – постоянная Больцмана. Для жестких молекул, у которых не возбуждены колебательные степени свободы, существует всего три значения
Дж/К – постоянная Больцмана. Для жестких молекул, у которых не возбуждены колебательные степени свободы, существует всего три значения  :
:
для одноатомных молекул  ;
;
для двухатомных молекул;  ;
;
для трех- и более атомных молекул  .
.
Внутренняя энергия идеального газа это суммарная кинетическая энергия всех молекул:  , (5.3)
, (5.3)
Примерами одноатомных молекул могут быть молекулы таких газов, как гелий  , неон
, неон  , аргон
, аргон  , криптон
, криптон  , ксенон
, ксенон  – благородные газы. Двухатомные молекулы у молекулярного водорода
– благородные газы. Двухатомные молекулы у молекулярного водорода  , кислорода
, кислорода 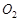 , азота
, азота  . Трехатомные молекулы у углекислого газа
. Трехатомные молекулы у углекислого газа  , водяного пара
, водяного пара  , озона
, озона  . Многоатомные молекулы у метана
. Многоатомные молекулы у метана  , этилового спирта (этанола)
, этилового спирта (этанола)  и т.д.
и т.д.
Если изменять объем газа, то газ при этом совершает работу:
|
|
|
 . (5.4)
. (5.4)
Из (5.4) видно, что работа газа при расширении положительная, а при сжатии – отрицательная. Если объем газа не менятся (изохорический процесс), то газ работу не совершает.
Первое начало термодинамики: тепло, данное газу, идет на изменение внутренней энергии газа и на совершение газом работы над внешними телами.  , (5.5)
, (5.5)
где  – изменение внутренней энергии идеального газа,
– изменение внутренней энергии идеального газа,  – элементарная работа газа при изменении объема на малую величину
– элементарная работа газа при изменении объема на малую величину  .
.
Теплоемкостью газа называется величина, характеризующая количество тепла, необходимое для нагревания всего газа на 1 К.
 (5.6)
(5.6)
В зависимости от способа изменения состояния газа, теплоемкость может принимать разные значения и даже может быть функцией температуры  . Если теплоемкость газа является постоянной величиной
. Если теплоемкость газа является постоянной величиной 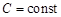 , то такой поцесс называется политропическим.
, то такой поцесс называется политропическим.
В качестве примера политропического процесса можно привести изохорический процесс с теплоемкостью
 , (5.7)
, (5.7)
изобарический процесс с теплоемкостью
 (5.8)
(5.8)
Из (5.6) следует, что при известной зависимости  можно найти тепло
можно найти тепло  , необходимое для нагревания газа от тепературы
, необходимое для нагревания газа от тепературы  до
до  :
:
 (5.9)
(5.9)
5.1. Сколько тепла надо сообщить m = 220 г углекислого газа, чтобы при неизменной температуре t 0 = 27 0 С расширить его в e2 = (2,72)2 раз? Ответ: Q = 24,93 кДж.
 5.2. Идеальный одноатомный газ в количестве 4 моль находится в сосуде под незакреплённым поршнем массы m = 1 кг и площади S = 0,1 м 2. Газу сообщено тепло Q = 1001 Дж. На какую высоту h поднялся поршень?
5.2. Идеальный одноатомный газ в количестве 4 моль находится в сосуде под незакреплённым поршнем массы m = 1 кг и площади S = 0,1 м 2. Газу сообщено тепло Q = 1001 Дж. На какую высоту h поднялся поршень?
Атмосферное давление p а = 10 5 Па, g = 10 м/с 2.
Ответ: 
5.3. Какую работу надо совершить над m = 16 г кислорода, чтобы очень быстро (адиабатически) охладить его на  ? (415,5 Дж.)
? (415,5 Дж.)
5.4. Некоторое количество идеального газа имело объём 1 л и давление 105 Па. Какую работу совершает этот газ, расширяясь до вдвое большего объёма в процессе T/V 2 = const? Ответ:  .
.
5.5. Один моль идеального газа совершает процесс  , где b = const. Чему равна теплоемкость газа в этом процессе? (
, где b = const. Чему равна теплоемкость газа в этом процессе? ( )
)
|
|
|
5.6. Теплоемкость одного моля идеального одноатомного газа зависит от температуры по закону  , где
, где  Дж/К,
Дж/К,  К.
К.
Найти работу, совершенную газом, при изменении температуры газа от  до
до 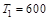 К. Универсальная газовая постоянная R = 8,3 Дж/моль×К;
К. Универсальная газовая постоянная R = 8,3 Дж/моль×К;
Ответ: –2334 Дж
Качественные задачи
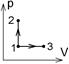
 5.7к. Идеальный газ совершает циклический процесс 1-2-3-1, как показано на рисунке, где процессы 2-3 – изохорический, а 3-1 – изотермический. Площадь
5.7к. Идеальный газ совершает циклический процесс 1-2-3-1, как показано на рисунке, где процессы 2-3 – изохорический, а 3-1 – изотермический. Площадь  фигуры 1-2-3 равна 10 Дж, а площадь
фигуры 1-2-3 равна 10 Дж, а площадь  фигуры 1-3-В-А равна 15 Дж. В процессе 3-1 газ отдал окружающей среде тепло...
фигуры 1-3-В-А равна 15 Дж. В процессе 3-1 газ отдал окружающей среде тепло...
Ответ: 15 Дж
 5.8к. На диаграмме (p, V) изображен цикл Карно для идеального газа. Для величины работы адиабатического расширения газа
5.8к. На диаграмме (p, V) изображен цикл Карно для идеального газа. Для величины работы адиабатического расширения газа  и адиабатического сжатия
и адиабатического сжатия  справедливо утверждение...
справедливо утверждение...
а) работы невозможно сравнить
б) 
в) 
 г)
г) 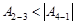
5.9к. Молярные теплоемкости азота в процессах  и
и  равны
равны  и
и  соответственно. Их отношение
соответственно. Их отношение  равно: а)
равно: а)  б)
б) 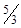 в)
в)  г)
г) 
5.10к. Средняя кинетическая энергия молекул газа при температуре Т зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место только поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекулы азота 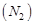 равна... а)
равна... а)  б)
б)  в)
в)  г)
г) 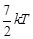
5.11к. Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты  . На увеличение внутренней энергии газа расходуется часть теплоты
. На увеличение внутренней энергии газа расходуется часть теплоты  , равная в процентах...
, равная в процентах...
 5.12к. Если не учитывать колебательные движения в линейной трехатомной " молекуле" газа (см.рис.), то отношение кинетической энергии вращательного движения к полной кинетической энергии молекулы равно...а)
5.12к. Если не учитывать колебательные движения в линейной трехатомной " молекуле" газа (см.рис.), то отношение кинетической энергии вращательного движения к полной кинетической энергии молекулы равно...а) 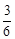 б)
б)  в)
в)  г)
г) 
5.13к. Молярная теплоемкость идеального газа при постоянном давлении равна  , где
, где  Дж/(кг×моль) – универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно..
Дж/(кг×моль) – универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно..
а) 9 б) 1 в) 2 г) 3
|
|
|


