 |
Законы сохранения импульса, момента импульса
|
|
|
|
И механической энергии
Исходя из закона изменения импульса (2.1), можно рассмотреть частный случай, когда сумма внешних сил равна нулю. Тогда импульс системы не изменяется во времени (закон сохранения импульса):
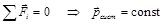 (3.1)
(3.1)
Исходя из закона изменения момента импульса (2.3), можно рассмотреть частный случай, когда сумма внешних моментов сил равна нулю. Тогда момент импульс системы не изменяется во времени (закон сохранения момента импульса):
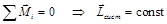 (3.2)
(3.2)
Очень часто в физических задачах рассматривается модель очень краткого взаимодействия двух или нескольких тел (столкновение двух тел в полете, взрыв сняряда и разлет осколков, столкновение свободного тела с телом, подвешенным на шарнире, и т.д.). Если в таких ситуациях результирующая сила или момент сил за время столкновения не существенно изменяют импульс (2.2) или момент импульса (2.4), то законы (3.1) и (3.2) можно считать почти точными.
В случаях существенного изменения импульса или момента импульса остается возможность применения законов сохранения (3.1) и (3.2) только в проекции на ось, проекция результирующей силы или момента силы на которую равны нулю:
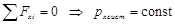 (3.3)
(3.3)
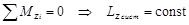 (3.4)
(3.4)
Третьим основным законом механики является закон изменения полной механической энергии системы  , где
, где 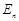 – потенциальная энергия системы тел,
– потенциальная энергия системы тел, 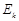 – кинетическая энергия этой системы:
– кинетическая энергия этой системы:
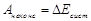 , (3.5)
, (3.5)
где 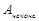 – работа неконсервативных сил.
– работа неконсервативных сил.
Если работа неконсервативных сил равна нулю, то выполняется закон сохранения механической энергии:
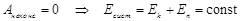 (3.6)
(3.6)
В механических задачах чаще всего учитываются два типа потенциальных энергий и два типа кинетических.
Гравитационная потенциальная энергия и потенциальная энергия упругой деформации
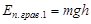 или
или 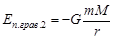
 (3.7)
(3.7)
где  – высота центра масс тела над произвольным нулевым уровнем,
– высота центра масс тела над произвольным нулевым уровнем,  – масса тела,
– масса тела, 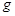 – ускорение свободного падения,
– ускорение свободного падения, 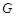 – гравитационная постоянная,
– гравитационная постоянная, 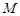 – масса планеты,
– масса планеты, 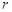 – расстояние от центра планеты до центра масс тела,
– расстояние от центра планеты до центра масс тела,  – коэффициент жесткости пружины,
– коэффициент жесткости пружины, 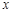 – деформация пружины.
– деформация пружины.
|
|
|
Понятие потенциальной энергии связано с выделением особых консервативных сил. Связь между консервативной силой и потенциальной энергией задается оператором "набла", действие которого на скалярную функцию 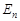 называется градиентом потенциальной энергии:
называется градиентом потенциальной энергии:
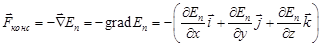 , (3.8)
, (3.8)
Кинетическая энергия поступательного и вращательного движения
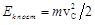 ,
,  (3.9)
(3.9)
где  – скорость центра масс системы тел с суммарной массой
– скорость центра масс системы тел с суммарной массой  ,
,
 – момент инерции системы тел относительно оси вращения (2.5), проходящей через центр масс С этой системы, w – угловая скорость вращения вокруг этой оси (чаще всего для системы из одного вращающегося тела).
– момент инерции системы тел относительно оси вращения (2.5), проходящей через центр масс С этой системы, w – угловая скорость вращения вокруг этой оси (чаще всего для системы из одного вращающегося тела).
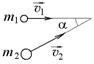 3.1. Маленький пластилиновый шарик массы m 1 = 0,1 кг движется горизонтально со скоростью
3.1. Маленький пластилиновый шарик массы m 1 = 0,1 кг движется горизонтально со скоростью  1 м/с. Под углом a = 30° к направлению его движения летит второй шарик массы m 2 = 0,2 кг со скоростью
1 м/с. Под углом a = 30° к направлению его движения летит второй шарик массы m 2 = 0,2 кг со скоростью 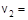 2 м/с и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения первого шарика. Найдите
2 м/с и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения первого шарика. Найдите 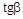 . Ответ: 0,448
. Ответ: 0,448
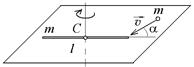 3.2. На горизонтальной плоскости лежит тонкий однородный стержень массы m =0,1 кг и длины l = 1 м, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью
3.2. На горизонтальной плоскости лежит тонкий однородный стержень массы m =0,1 кг и длины l = 1 м, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью 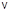 = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара. Ответ: 0,75 рад/с.
= 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара. Ответ: 0,75 рад/с.
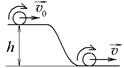 3.3. Тонкий однородный диск массы m = 1 кг и радиуса R = 1 мскатывается без проскальзывания с горки высоты h = 1 м, совершая плоское движение. Начальная скорость центра масс диска равна
3.3. Тонкий однородный диск массы m = 1 кг и радиуса R = 1 мскатывается без проскальзывания с горки высоты h = 1 м, совершая плоское движение. Начальная скорость центра масс диска равна 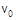 = 1 м/с. Сопротивление воздуха пренебрежимо мало, g = 10 м/с2. Найдите скорость центра масс диска, после того, как он скатится с горки. Ответ: 3,79 м/с;
= 1 м/с. Сопротивление воздуха пренебрежимо мало, g = 10 м/с2. Найдите скорость центра масс диска, после того, как он скатится с горки. Ответ: 3,79 м/с;
|
|
|
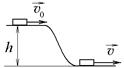 3.4. Резиновая шайба массы m = 1 кг, двигаясь со скоростью
3.4. Резиновая шайба массы m = 1 кг, двигаясь со скоростью 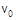 = 1 м/с, соскальзывает с горки высоты h = 1 м и приобретает скорость
= 1 м/с, соскальзывает с горки высоты h = 1 м и приобретает скорость 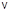 у подножия горки. Во время движения над шайбой была совершена работа сил трения, модуль которой равен А тр=1 Дж (g = 10 м/с2).Найдите скорость шайбы
у подножия горки. Во время движения над шайбой была совершена работа сил трения, модуль которой равен А тр=1 Дж (g = 10 м/с2).Найдите скорость шайбы 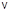 Ответ: 4,36 м/с
Ответ: 4,36 м/с
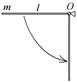 3.5. Тонкий однородный стержень массы m = 1 кги длины l = 1 м может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через конец стержня О. Стержень приводят в горизонтальное положение и отпускают без толчка. Сопротивление воздуха пренебрежимо мало, g = 10 м/с2. В момент прохождения им положения равновесия найдите скорость нижнего конца стержня. (5,48 м/с)
3.5. Тонкий однородный стержень массы m = 1 кги длины l = 1 м может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через конец стержня О. Стержень приводят в горизонтальное положение и отпускают без толчка. Сопротивление воздуха пренебрежимо мало, g = 10 м/с2. В момент прохождения им положения равновесия найдите скорость нижнего конца стержня. (5,48 м/с)
Качественные задачи.
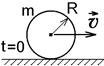 3.6к.. В начальный момент времени t = 0 тонкий обруч с массой m = 0,1 кг и с радиусом R = 0,5 м не вращался, а поступательно скользил по горизонтальной поверхности с кинетической энергией 800 Дж. Под действием силы трения он начал катиться без проскальзывания с кинетической энергией поступательного движения 200 Дж. Сила трения совершила работу:
3.6к.. В начальный момент времени t = 0 тонкий обруч с массой m = 0,1 кг и с радиусом R = 0,5 м не вращался, а поступательно скользил по горизонтальной поверхности с кинетической энергией 800 Дж. Под действием силы трения он начал катиться без проскальзывания с кинетической энергией поступательного движения 200 Дж. Сила трения совершила работу:
а) 300 Дж б) 600 Дж в) 500 Дж г) 400 Дж
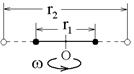 3.7к. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r1 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости w, при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние r2 = 2r1 и раскрутили до той же угловой скорости. Какая работа при этом была совершена?
3.7к. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r1 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости w, при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние r2 = 2r1 и раскрутили до той же угловой скорости. Какая работа при этом была совершена?
1) А2 = 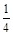 А1 2) А2 = 2А1 3) А2 =
А1 2) А2 = 2А1 3) А2 =  А1 4) А2 = 4А1
А1 4) А2 = 4А1
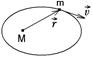 3.8к. Планета массой
3.8к. Планета массой  движется по эллиптической орбите, в одном из фокусов которой находится звезда массы
движется по эллиптической орбите, в одном из фокусов которой находится звезда массы  .
. 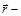 радиус-вектор планеты (см.рисунок). Выберите правильное утверждение:
радиус-вектор планеты (см.рисунок). Выберите правильное утверждение:
а) момент импульса планеты относительно центра звезды меняется и максимален при наибольшем ее удалении 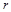 от звезды
от звезды
б) момент силы тяготения, действующей на планету (относительно центра звезды), изменяется, но направлен перпендикулярно плоскости орбиты
в) величина момента импульса планеты относительно центра звезды в любой момент времени определяется выражением 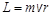
|
|
|
г) момент импульса планеты относительно центра звезды не изменяется
 3.9к. Два невесомых стержня длины b соединены под углом a1 = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a2 = 120°. С какой угловой скоростью стала вращаться такая система? 1) 3w 2)
3.9к. Два невесомых стержня длины b соединены под углом a1 = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a2 = 120°. С какой угловой скоростью стала вращаться такая система? 1) 3w 2) 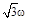 3)
3) 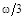 4)
4)  5) w
5) w
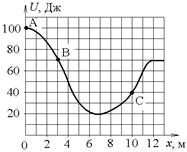 3.10к. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике
3.10к. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике  . Кинетическая энергия шайбы в точке С
. Кинетическая энергия шайбы в точке С
а) в 2 раза больше, чем в точке В
б) в 2 раза меньше, чем в точке В
в) в 1,75 раза больше, чем в точке В г)в 1,75 раза меньше, чем в точке В
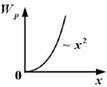 3.11к. На рисунке показан график зависимости потенциальной энергии
3.11к. На рисунке показан график зависимости потенциальной энергии 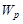 от координаты х. График зависимости проекции силы
от координаты х. График зависимости проекции силы 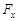 от координаты х имеет вид...
от координаты х имеет вид...
а)  б)
б) 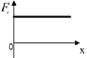 в)
в) 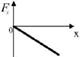 г)
г) 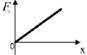
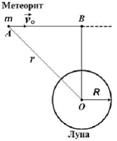 3.12к. Находясь на расстоянии
3.12к. Находясь на расстоянии 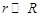 , по направлению к Луне летит метеорит, скорость которого
, по направлению к Луне летит метеорит, скорость которого 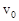 . Для расчета минимального прицельного расстояния ОВ, при котором метеорит не упадет на поверхность Луны, используют законы сохранения механической энергии и момента импульса. Выберите из предложенных вариантов верную запись этих законов. Радиус
. Для расчета минимального прицельного расстояния ОВ, при котором метеорит не упадет на поверхность Луны, используют законы сохранения механической энергии и момента импульса. Выберите из предложенных вариантов верную запись этих законов. Радиус 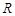 и массу
и массу 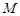 Луны, гравитационную постоянную
Луны, гравитационную постоянную 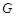 , скорость метеорита вблизи поверхности Луны
, скорость метеорита вблизи поверхности Луны 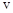 считать известными.
считать известными.
а) 
б) 
в) 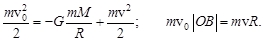
3.13к. Кинетическая энергия тела (спутника), движущегося по круговой орбите вокруг Земли, меньше его гравитационной потенциальной энергии, взятой по модулю в ______ раза.
3.14к. Шарик массой  упал с высоты
упал с высоты 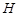 на стальную плиту и упруго отскочил от нее вверх. Изменение импульса шарика в результате удара равно...
на стальную плиту и упруго отскочил от нее вверх. Изменение импульса шарика в результате удара равно...
а) 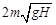 б)
б) 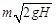 в)
в) 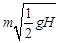 г)
г) 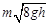
 3.15к. Экспериментатор, стоящий на неподвижной скамье Жуковского, получает от помощника колесо, вращающееся вокруг вертикальной оси с угловой скоростью w. Если экспериментатор повернет ось вращения колеса на угол 180°, то он вместе с платформой придет во вращение с угловой скоростью w/5. Отношение момента инерции экспериментатора со скамьей к моменту инерции колеса равно... а) 10 б) 2,5 в) 5 г) 4
3.15к. Экспериментатор, стоящий на неподвижной скамье Жуковского, получает от помощника колесо, вращающееся вокруг вертикальной оси с угловой скоростью w. Если экспериментатор повернет ось вращения колеса на угол 180°, то он вместе с платформой придет во вращение с угловой скоростью w/5. Отношение момента инерции экспериментатора со скамьей к моменту инерции колеса равно... а) 10 б) 2,5 в) 5 г) 4
|
|
|
|
|
|


