 |
Открытая транспортная задача
|
|
|
|
При открытой транспортной задаче сумма запасов не совпадает с суммой потребностей, т.е. 
≠ 
.
При этом возможны два варианта:
а) если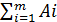 
< 
, то объем запасов превышает объем потребления,все потребители будут удовлетворены полностью и часть запасов останется не вывезенойю Для решения задачи вводят фиктивного (n+1) потребителя, потребности которого Bn+1 = 
Модель Такой задачи будет иметь вид F(x) =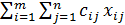 
min при ограничениях:
,
Xij≥ 0, j=1,n+1, j=1,n;
б)если <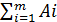 
то объем потребления превышает объем запасов, часть потребностей останется неудовлетворенной. Для решения вводим фиктивного (m+1) поставщика.
Am+1= - 
Модель такой задачи имеет вид: 
min
При ограничениях:
,
Xij≥ 0, i = 1,m+1, j =1,n.
При введении фиктивных поставщика или потребителя открытая транспортная задача становится закрытой и решается по ранее рассмотренному алгоритму для закрытых транспортных задач, причем тарифы, соответствующие фиктивному поставщику или потребителю, принимаются больше или равными наибольшему из всех транспортных тарифов, иногда их считают равными нулю. В решении целевой функции фиктивный поставщик или потребитель не учитываются.
Пример 9. Составить оптимальный план перевозки грузов от трех поставщиков с грузами 240, 40, 110 т к четырем потребителям с запросами 90, 190, 40 и 130 т. Стоимости перевозок единицы груза от каждого поставщика к каждому потребителю заданы матрицей.
Решение. Запасы грузов у поставщик: 
= 390т. Запросы
потребителей: 
= 450т, так как < 
, то вводим фиктивного поставщика с грузом а4ф= 450 – 390 = 60т.
Тариф фиктивного поставщика 4ф примем равным 0 ден.ед.
Составим опорный план методом минимальной стоимости.
| bj ai | αi | |||||
| 130 | +3 9 | |||||
| -5 | ||||||
| -2 | ||||||
| 4ф | -13 | |||||
| βj |
Так как m+n–1=7, а число занятых клеток равно 6, то для исключения вырожденности введем в клетку (2,2) нулевую поставку. Оценки ∆1,1= –2, ∆1,3 = 3, ∆2,1= –14, ∆2,4 = –7, ∆3,3 = –10, ∆4ф1= –8, ∆4ф3= –1,∆4ф4= –5. Для клетки (1,3), имеющую положительную оценку строим контур и перераспределяем грузы.
|
|
|
| – |
| + |
| + |
| – |
| (2.2) |
| (1.2) |
| (1.3) |
| (2.3) |
Получаем новый план.
| Bj Ai | αi | |||||
| -5 | ||||||
| -2 | ||||||
| 4ф | -13 | |||||
| βj |
∆11= -2, ∆21= -14, ∆23=-3, ∆24=-7, ∆32=-4, ∆33=-13, ∆41=-8, ∆43=-4, ∆44=-5.
Таким образом, мы получили оптимальное решение.
.
Стоимость транспортных расходов составляет: (Xопт) = 3120 ден.ед.
Варианты контрольной работы.
Классическая транспортная задача.
Решить транспортную задачу. С-матрица стоимостей. Прочерк означает невозможность перевозки по данному маршруту;
ai- запасы поставщиков, bj- заявки потребителей
1. С = 
2.С = 
3. С = 
4. С = 
5. С =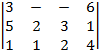 
6. С = 
7. С = 
8. С = 
9.С = 
10. С = 
11.С = 
12. С = 
13. С =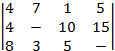 
14. С = 
15. С = 
16. С = 
17. С =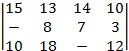 
18.С = 
19. С = 
20.С = 
21. С = 
22. С = 
23. С = 
24. С = 
25. С = 
26. С = 
27. С = 
28. С = 
29. С = 
30. С = 
| A1 | A2 | A3 | B1 | B2 | B3 | B4 | |
Транспортная параметрическая задача
|
|
|
Формулировка классической транспортной задачи имеет вид:
→ min
При ограничениях:
xij³0
Задача формулируется следующим образом: для всех значений параметра d£l£j, где d,j - произвольные действительные числа, найти такие значения xij (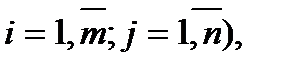
которые обращают в минимум функцию
= 
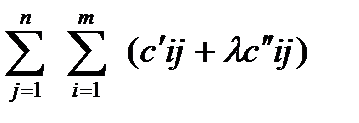
При ограничениях:
,
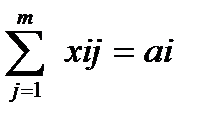
xij³0, 
Пользуясь методом потенциалов, решаем задачу приl=d до получения оптимального решения. Признаком оптимальности являются условия:
ai+bj – (c¢ij+ dc²ij)£0 для незанятых клеток,
ai+bj = c¢ij+ dc²ij для занятых клеток,
где ai и bj– потенциалы строк и столбцов.
Оценки представим в виде ∆ij=μij + lυij
Значения l находятся в пределах l1£l£l2:
max 
если существует хотя бы одно 
<0,
l1=
¥, если все ≥0.
min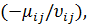 
если существует хотя бы одно >0,
l2=
¥, если все £0.
Алгоритм решения задачи:
1. Задачу решаем при конкретном значении параметра l=d до получения оптимального решения.
2. Определяем 
|
|
|
