 |
Оптимальное исследование рынка
|
|
|
|
Группе, исследующей рынок, требуется получить данные из n различных мест. В ее распоряжении имеется n дней, и она предполагает провести по одному дню в каждом месте, проведя по ajопросов, j=1,…,n. Вероятность успешного опроса в каждом месте задается матрицей Р. Элемент матрицы pijхарактеризует вероятность успешного опроса в течении i-го дня в j-ом месте, i=1,…,n.
Определить время проведения опросов, при котором общее число опросов максимально.
Сведем данную задачу к задаче о назначениях.
Введем величину rij=pijaj, показывающую число успешных опросов в j-ом месте в течение i-го дня.
1, если в i-й день опрос проводится в j-ом месте;
хij=
0, в противном случае.
Математическая модель задачи имеет следующий вид:





Функция F характеризует суммарное число успешных опросов. Ее нужно максимизировать. Первое и второе ограничения соответствуют тому, что в течение одного дня можно находиться только в одном месте. Для расчета модели венгерским методом надо перейти к противоположной функции
и в соответствующей таблице записывать значение rijс противоположным знаком.
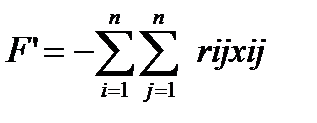
Оптимальное использование торговых агентов
Торговая фирма продает товары в nразличных городах, покупательная способность жителей которых оценивается bjусл.ед., j=1,…,n. Для реализации товаров фирма располагает n торговыми агентами, каждого из которых она направляет в один из городов. Профессиональный уровень агентов различен; доля реализуемых i-ым торговым агентом покупательных способностей составляет ai, i=1,…,n. Как следует распределить торговых агентов по городам, чтобы фирма получила максимальную выручку от продажи товаров?
Решение этой проблемы может быть найдено с помощью задачи о назначениях.
|
|
|
В качестве кандидатов выступают торговые агенты, в качестве работ - города.
Введем параметр cij=aibj, характеризующий величину покупательных способностей, реализуемых i-ом торговым агентом в j-ым городе.
Управляющие переменные xij, i=1,…,n; j=1,…,n определяются по формуле
1, если i-й агент направлен в j-й город;
xij=
0, в противном случае.
Математическая модель запишется в следующей форме:

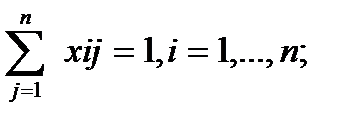


Первое и второе ограничения формализуют соответственно условию о том, что в каждый город направляется один торговый агент и один торговый агент не может работать в двух городах. Целевая функция F - это сумма реализованных покупательных способностей всеми торговыми агентами во всех городах. Она должна подлежать максимизации. Для решения задачи венгерским методом надо, как и в предыдущем примере, перейти к противоположной функции.
Задача о диете
Задачей о диете называется задача линейного программирования, состоящая в определении такого рациона (набора продуктов питания), которой удовлетворял бы потребности человека (например, при питании работников некоторого предприятия) в необходимых питательных веществах при минимальной общей стоимости приобретаемых продуктов питания. Эта задача является частным случаем более общей задачи об оптимальном составе смеси.
В общем виде задача о диете формулируется следующим образом. Пусть xj– количество продукта питания j-го вида; cj – цена единицы продукта j-го вида;n – количество видов продуктов питания  Известны нормы потребления (не менее) каждого из m типов питательных веществ, которые обозначены bi
Известны нормы потребления (не менее) каждого из m типов питательных веществ, которые обозначены bi  и содержание питательных веществ каждого типа в единице продукта каждого вида, которое обозначается величиной aij. Требуется определить количество продуктов питания каждого вида, обеспечивающих нормы потребления всех питательных веществ имеющих наименьшую стоимость. Экономико-математическая модель данной задачи имеет вид:
и содержание питательных веществ каждого типа в единице продукта каждого вида, которое обозначается величиной aij. Требуется определить количество продуктов питания каждого вида, обеспечивающих нормы потребления всех питательных веществ имеющих наименьшую стоимость. Экономико-математическая модель данной задачи имеет вид:
|
|
|


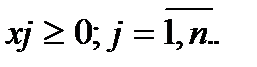
|
|
|


