Параметры течения газовых потоков и связь между ними

Лекция 1 Вводная

Введение

Гидродинамика - наука, изучающая законы движения несжимаемой и сжимаемой жидкости (газа). Развитие этой науки проходило как решение проблем, связанных с определением силы сопротивления, оказываемого жидкой (газообразной) средой движущемуся в ней телу. Не останавливаясь подробно на истории гидроаэродинамики отметим некоторые этапы развития этой науки. Первые успехи теории сопротивления, относящиеся к ХVII в., были достигнуты благодаря изучению закона падения тел и движения маятника, который служил в то время инструментом для измерения времени. На основе своих опытов Галилей впервые показал, что сопротивление, испытываемое телом, движущимся в жидкой среде, возрастает с увеличением плотности среды и скорости движения. Количественную оценку величины сопротивления Галилей не произвел. В конце ХVII и начале ХVIII в. в изучение проблемы сопротивления большой вклад внес Исаак Ньютон. Исследуя движение шара в различных средах, Ньютон установил, что сопротивление шара R пропорционально плотности среды, квадрату скорости движения v и площади сечения S. Таким образом, был открыт основной закон сопротивления: , при этом для шара С= 0.5. В своих теоретических работах Ньютон особенно подробно исследовал движение гипотетической жидкости, состоящей из дискретных частиц. Применительно к ней Ньютон создал так называемую ударную теорию сопротивления пластинки, движущейся под некоторым углом атаки. Применяя теорему о количестве движения, он определил величину силы сопротивления. Ньютон полагал, что масса жидкости, набегающей за единицу времени на пластинку площадью S под углом атаки равна , а нормальная составляющая скорости частиц жидкости к пластине, равная , полностью теряется при ударе жидкости об эту пластину. Ньютон получил следующую формулу для силы сопротивления R, нормальной к поверхности пластины: . Величина подъемной силы крыла, полученная в соответствии с полученной формулой, была настолько мала, что долгое время этот факт приводился в качестве доказательства неосуществимости полета аппаратов тяжелее воздуха.

В настоящее время при макроскопическом выводе уравнений движения жидкости выделяется элементарный объем, к которому приложены поверхностные и объемные силы, и используется второй закон Ньютона для вычисления его ускорения. При этом в основе системы аксиом Ньютона лежит базисный эксперимент по соударению двух точечных масс, моделирующийся упругим соударением двух шаров [19]. Для жидкостей и газов такого базисного эксперимента нет. Хотя сам И.Ньютон в работе «Математические начала натуральной философии» отмечал «Жидкость есть такое тело, коего части уступают всякой как бы то ни было приложенной силе и, уступая, свободно движутся друг относительно друга», уравнения движения жидкости и газа, в основу которых положены законы сохранения Ньютона, позволили в значительной степени изучить многие явления природы, достичь технического прогресса и, что немаловажно, дать толчок в развитии многих важных разделов математики.

В XVIII в. учение о сопротивлении стимулировалось главным образом развитием мореплавания, гидроэнергетики и артиллерии. Развитие мореходства выдвинуло задачу об определении сопротивления корабля, что заставило ученых более детально заняться вопросами обтекания. В 1763 г. капитан французского флота Борда провел многочисленные опыты по определению сопротивления различных тел в воздухе и в воде. Борда подтвердил квадратичный закон сопротивления Ньютона и одновременно, в чем его огромная заслуга, показал, что ударная теория Ньютона дает слишком заниженные значения подъемной силы. В результате чего вновь возродился интерес к проблеме создания летательных аппаратов тяжелее воздуха.

С середины XVIII в. развернулись теоретические исследования по изучению движения жидкости, положившие начало теоретической гидродинамике. Честь ее создания принадлежит Российской Академии наук в лице Леонарда Эйлера и Даниила Бернулли. В труде «Общие принципы движения жидкостей» Л. Эйлер впервые вывел основные дифференциальные уравнения движения так называемой «идеальной жидкости», положив начало важнейшей отрасли механики сплошной среды - гидроаэродинамике. Л. Эйлеру гидроаэродинамика обязана, в частности, введением понятия давления. Д. Бернулли принадлежит открытие фундаментального закона гидродинамики, устанавливающего связь между давлением и скоростью в потоке несжимаемой жидкости, обобщенного ныне для случая сжимаемой жидкости.

Дальнейшее развитие аналитические методы гидродинамики получили в трудах известного французского ученого Лагранжа, давшего новую форму дифференциальных уравнений гидродинамики и разработавшего теорию потенциального движения жидкости.

Как самостоятельная наука теоретическая гидродинамика начала складываться в первой половине ХIХ в.. Стало формироваться теоретическое направление, цель которого описать поведение жидкости и газов и их взаимодействие с телами путем построения адекватных моделей. Поставленная Даламбером задача о теоретическом определении силы сопротивления тела, обтекаемого потенциальным (безвихревым) потоком идеальной жидкости, привела к неожиданному результату: сила сопротивления оказалась равной нулю. Этот результат носит название парадокса Даламбера. Указанное обстоятельство сыграло роль своеобразного тупика, в котором очутилась теория идеальной жидкости при определении силы сопротивления.

Значительно позже известные немецкие ученые Гельмгольц и Кирхгофф вновь сделали попытку использовать модель идеальной жидкости, предложив совершенно иную модель обтекания со срывом струй. Эта теория позже была развита и усовершенствована в работах Жуковского, Леви- Чивита и Вилля, а далее в работах А.И. Некрасова, Н.С. Аржанникова, Н.А. Слезкина и др.

В начале ХIХ в. в работах С. Пуассона, Дж. Стокса, Р. Ирншоу были впервые теоретически проанализированы нелинейные эффекты, возникающие при распространении волн давления в сжимаемой среде.

Во второй половине ХIХ в. в работах Б. Римана, а затем Ж. Адамара нелинейная теория распространения волн в сжимаемой среде была доведена до совершенства. В. Рэнкин и А. Гюгонио заложили основы движения сжимаемых сред с разрывами параметров.

В 1826 г. французский ученый Навье получил впервые дифференциальные уравнения движения вязкой жидкости, основываясь на ряде физических гипотез. В 1846г. английский гидродинамик Стокс дал строгий вывод этих уравнений, в силу чего они известны как уравнения Навье- Стокса. При феноменологическом выводе уравнений Навье- Стокса, используются два главных допущения:

а) о тензорном законе вязкого сопротивления, обобщающем закон Ньютона;

б) о короткодействии внутренних сил в элементарном объеме, которые, следовательно, сводятся к силам поверхностным. При принятом условии компоненты тензора напряжений не зависят от порядка индексов, т.е. тензор напряжений симметричен. При малых числах Рейнольдса это вполне оправдано. Однако турбулентность в потоке опровергает это допущение. Кроме того, по определению - элементарный объем это такой малый объем, в котором сохраняются основные свойства макроскопического процесса и (в газовой динамике) свойство короткодействии сил применимо лишь с оговорками.

Турбулентное течение характеризуется заметным вихревым течением с вихрями самых разных масштабов. Подробный обзор стоящих здесь проблем дан Белоцерковским О.М. в книге [18]. Для практического решения задачи о движении турбулентных течений, как правило, вводится допущение о локальной изотропии механизма турбулентного перемешивания. Изотропия позволила получить все тензоры аналогичные случаю только молекулярной вязкости. Опираясь на аналогию между ламинарным и осредненным турбулентным течением Ж. Буссинеск (1877) по аналогии с первым предложил формулу для касательного напряжения, похожую на формулу Ньютона, . Здесь вместо обычной молекулярной вязкости употребляется коэффициент турбулентной (молярной) вязкости «А» [6]. Величина «А» определяется на основе различных полуэмпирических подходов. Неадекватность модели Буссинеска физическому процессу очевидна. Такой подход не отражает многие свойства турбулентных потоков (с крупномасштабными пульсациями). В частности, не учитывается свойство анизотропии крупномасштабных вихрей. Поэтому аппроксимации величины «А» не могут носить общий характер. Следовательно, внесение дополнительных поправок в такую модель, видимо, только усложняет задачу и не решают проблему в целом. Однако для решения ряда задач этот подход позволяет получить приемлемые результаты. Поэтому теории, построенные на «моделях турбулентности» все еще имеют широкое распространение.

В конце ХIХ в. при исследовании движений сжимаемых сред стала ясной необходимость использования представлений термодинамики, причем не только ее первого начала, которое выражает закон сохранения энергии, но и второго начала - закона не убывания энтропии в замкнутых адиабатических системах.

С начала XX в. и до середины 30-х годов в теоретической газовой динамике шло накопление фактов, вызванные потребностями практики создавались теории обтекания крыла бесконечного размаха и тел вращения, движения газа в межлопаточных каналах турбины и соплах. В связи с ростом интереса к проблемам авиации, т.е. к изучению движения тел в вязкой жидкости с относительно большими скоростями, теория Навье- Стокса значительно продвинулась вперед благодаря работам Л. Прандтля, предложившего в 1904 г. модель пограничного слоя, которая явилась большим вкладом в теорию сопротивления.

Огромная роль в развитии отечественной и мировой аэродинамики принадлежит Н.Е. Жуковскому и С.А. Чаплыгину. Н.Е. Жуковским написан ряд работ, заложивших теоретические основы аэродинамики полета и крыла. Им разработаны методы экспериментальных исследований в аэродинамике. Отличительной особенностью работ С.А. Чаплыгина является общность даваемых им методов, что позволило ему и созданной им школе (А.И. Некрасов, В.В. Голубев, М.В. Келдыш, М.А. Лаврентьев, Л.И. Седов, Ф.И. Франкль, С.А. Христианович и др.) значительно продвинуть вперед разработку проблем современной аэродинамики. В последние годы продолжается стремительное развитие науки о газовой динамике, которая к середине 60-х годов превратилась в разветвленную область знания, составляющую основу ряда направлений естествознания и многих областей современной техники. Под воздействием потребностей газовой динамики происходило и происходит развитие асимптотических методов математики, вычислительной математики, вычислительной техники и др. На фундаменте классической газовой динамики в последние десятилетия интенсивно развиваются ее новые специальные разделы, например физико - химическая газодинамика. Она сама уже представляет совокупность ряда направлений, таких как:

гиперзвуковая газовая динамика, связанная с изучением полета тел в атмосфере Земли и других планет с очень большой скоростью. Здесь возникает высокая температура потока, обтекающего тело, которая делает необходимым учет химических превращений в газах;

радиационная газовая динамика, связанная также с гиперзвуковым полетом, с задачами горения газовых смесей, в которых необходимо учитывать процессы переноса лучистой энергии в газах;

релаксационная газовая динамика, в которой определяющую роль играет неравновесный характер протекающих в газе физико - химических процессов и другие разделы.

В представленном кратком обзоре не нашли своего отражения многие важные моменты развития аэродинамики. В частности, не прослежена история развития теории «вихря» и связанная с ней теория отрыва потока. С подробной историей развития науки можно познакомиться в [5,7,11].

На сегодня наука “газовая динамика” является математически одной из наиболее развитых и строго обоснованных.

Задача прикладной газовой динамики - построение адекватных приближенных математических моделей для решения практически важных частных задач в газовой динамике и изучение поведения газов в этих случаях. При составлении математической модели необходимо стремиться к тому, чтобы она отражала все наиболее существенные стороны процесса. С другой стороны, математическая модель должна быть достаточно простой для исследования, давать возможность извлечь из нее доступными средствами необходимую информацию о процессе. Поэтому какими-то факторами, влияние которых на процесс представляется малым, неизбежно приходится пренебрегать и они оказываются не представленными в математической модели процесса. Для уточнения «модели» часто прибегают к замене «неосновных факторов» их интегральной оценкой или «сглаженным» учетом при описании происходящего процесса [17].

Разделы газовой динамики и рассматриваемые в них задачи. Одним из важных разделов Г. д. является изучение т. н. внутренних течений газа в трубах и каналах, в частности в соплах и диффузорах реактивных двигателей и аэродинамич. труб. В приближённых методах исследования этих течений параметры газа считаются постоянными по сечению трубы или канала; изучаются течения в нек-рых газовых машинах, напр. в элементах компрессоров и газовых турбин, и др.

Широкий круг задач Г. д. связан с изучением внешнего обтекания тел газом. Для расчёта обтекания идеальным газом тонких тел, вносящих в поток лишь малые возмущения, разработаны методы, основанные на линеаризации ур-ний движения. Эти методы теряют силу при скоростях, близких к скорости звука (см. Околозвуковое течение), и при больших сверхзвуковых скоростях (см. Гиперзвуковое течение). При таких скоростях даже при обтекании тонких тел существенны нелинейные эффекты.

На основании установленных теоретич. путём законов подобия можно переносить результаты исследования обтекания одного тонкого тела при одном значении числа M на случаи обтекания других тел при том же значении числа M или того же тела при др. значениях числа M.

Расчёт обтекания сжимаемым газом тел конечной толщины вызывает значит. трудности. Получены точные решения лишь некоторых задач об обтекании при M >1 простейших тел, напр. круглого конуса и клина. В более сложных случаях течений около тел другой формы при М >1 с успехом используются численные методы расчёта, в частности метод характеристик, меток сеток и др. Дозвуковое течение (М <1) является более сложным для матем. исследования, что связано гл. обр. с трудностями при формулировании граничных условий для дифференц. ур-ний эллиптич. типа из-за того, что в дозвуковых потоках возмущения распространяются во все стороны.

Наиб. трудности связаны с изучением обтекания тел смешанным потоком, когда в части области, занятой движущимся газом, скорость газа больше скорости звука, а в др. части меньше её, что имеет место, напр., при сверхзвуковом обтекании тел, имеющих затупленную головную часть. В решении сложных задач Г. <д. имеются значит. успехи, связанные с использованием численных методов для решения систем конечно-разностных ур-ний, однако для многих важных задач Г. <д. всё ещё нет теорем о существовании, единственности и устойчивости решения.

Ещё одно направление газодинамич. исследований связано с задачами о неустановившихся движениях. К ним относятся, в частности, задачи внутр. баллистики, задачи о распространении и действии взрывных и детонационных волн, вопросы работы ударных труб, задачи о пульсациях давления и др. параметров в отрывных зонах, о нестационарных движениях газа в газопроводах и др. Mн. задачи об одномерных неустановившихся движениях могут быть решены численными методами. Большое значение для понимания качественных особенностей явлений имеют найденные точные решения задач о сильном точечном взрыве, о поведении произвольного разрыва в нач. распределениях параметров газа, о распространении сферич. детонационной волны и др. Важный раздел Г. д.- теория газовых струй. Теория турбулентных струй с учётом сжимаемости развивается, как и в случае несжимаемой жидкости, на полуэмпирич. основе. Она применяется, в частности, для расчёта эжекторов.

Учёт вязкости и теплопроводности газа в задачах об обтекании тел и в ряде задач о течениях газа в трубах и каналах производится во мн. случаях на основе теории пограничного слоя. В отличие от течений несжимаемой жидкости, в случае газа задачи об определении поверхностного трения и об определении темп-ры и тепловых потоков связаны друг с другом. Специфическим для околозвуковых и сверхзвуковых течений газа является взаимодействие между пограничным слоем и внеш. потоком, происходящее при отрыве пограничного слоя в месте, где возникающие в потоке скачки уплотнения приближаются к обтекаемой поверхности. При большой сверхзвуковой скорости значит. часть кинетич. энергии летящего тела переходит в теплоту, разогревая прилегающий к телу слой газа и обтекаемую поверхность (см. Аэродинамический нагрев). Толщина возмущённого слоя газа между поверхностью обтекаемого тела и ударной волной при этом может быть того же порядка, что и толщина вязкого слоя; поэтому в таком случае вязкость сильно влияет на всё возмущённое течение.

Целью решения всех перечисленных задач Г. д., как внутренних, так и внешних, является определение силового, теплового и физ.-хим. воздействия движущегося газа на омываемые им поверхности, а в нек-рых случаях - ещё и полных полей газодинамич. параметров во всей области течения.

Методы Г. <д. проникли в астрофизику и космогонию, где они применяются для решения задач о движениях космич. газовых масс и об их эволюции. При рассмотрении таких задач приходится учитывать действие гравитац. сил, а также действие на газ эл.-магн. полей. В связи с этими задачами, а также нек-рыми задачами о движении газа при высокой темп-ре, возникающими, напр., при создании магнитогазодинамич. генераторов электроэнергии или при решении проблемы управляемых термоядерных реакций, быстро развиваются разделы, связывающие Г. д. с электродинамикой и физикой высоких темп-р,- магнитная гидродинамика и динамика ионизованного газа (плазмы).

 

Параметры течения газовых потоков и связь между ними

 

Основные параметры, характеризующие состояние неподвижного (стационарного) газа:

Р - давление-

Паскаль:

1 Па = 1 н/м²; (Па, КПа, МПа)

- техническая атмосфера:

1 ат. = 9.81 10 ⁴ Па

- мм.рт.ст:

1 мм.рт.ст= 133 Па

физическая атмосфера:

1 атм.= 1.013 10⁵ Па

Бар

1 Бар = 10⁵ Па

Т- температура -

Градус Цельсия

1^оС

Градус Кельвина

1^oК

Градус Фаренгейта

1^оF ()

Градус Реомюра

1^оR

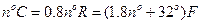
ρ- плотность

ρ(кг/м³)

ν- удельный объем

v=1/ρ (м³/кг)

 

Для идеального газа существует связь между данными параметрами (уравнение состояния идеального газа- уравнение Менделеева- Клайперона)

R- универсальная газовая постоянная (дж/кг ^оK)

Идеальный газ:

- отсутствует взаимодействие между молекулами не при каких условиях не рассматривается природа газа;

Влияние динамики потока и реальности газа:

*появляются силы взаимного притяжения молекул

123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: