 |
Уравнения количества движения газа в форме Л. Эйлера и И. Громеки
|
|
|
|
Многие практически важные реальные случаи сводятся к рассмотрению случаев течения потока идеального газа.
Для потока идеального газа:
- поток газа лишен сил трения
- отсутствует внутренний теплообмен и теплопроводность
(в потоке реального газа возникают градиенты температуры и совершается внутренний теплообмен между соседними частицами.
Переход рассмотрения процессов газодинамики к потоку идеального газа (отсутствует внутренний теплообмен и теплопроводность, изоэнтропийный процесс (отсутствуют потери энергии) и μ=0) позволяет уравнения Навье- Стокса об изменении количества движения для частицы газового потока преобразовать в уравнения Эйлера, полученные в 1759 г.:
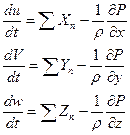
(5)
Уравнения могут быть представлены в развернутом виде;
(6)
Уравнения показывают, что ускорение частицы идеального газа вызывается соответствующими изменениями сил давления, действующих на элемент и силами внешних полей.
Переходя к рассмотрению движения потока идеального газа в цилиндрических координатах (r, θ, z) (тангенциальное ускорение, кариолисово ускорение), вводя в рассмотрение уравнения специфических элементов движения потока- компонентов вихря, потенциальной и кинетической энергии, некоторую функцию давления, выражающий потенциал объемного действия поверхностных сил давления
Некоторую потенциальную функцию U, частные производные от которой по координатам выражают проекции единичных массовых сил на оси координат
Профессор Казанского университета И. Громека в 1881 г. Вывел уравнения, названные в его честь:
(7)
Для установившегося движения (
, при отсутствии вихрей
(
Получим:
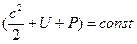(8)
|
|
|
Из данного уравнения в гидродинамике было получено уравнение Бернулли для несжимаемой жидкости:
. (9)
Уравнение моментов количество движения
Данный момент имеет особое значение при изучении вращательного движения газа.
Моментом количества движения относительно некоторой точки (оси вращения) называется произведение количества движения тела на кратчайшее расстояние от точки до линии, по которой направлена скорость.
o 
 |
1
r1
1’
r c1u
c1r 1
2 c1
C2u 1’
 |
C2 c2r 2’
Момент количества движения (1-1’):
(10)
Т.к. 
Для сечений 1-1’ 
По аналогии для сечения 2-2’ момент количества движения составит:
Разность моментов количества движения равен моменту импульса.
Момент импульса- произведение величины импульса на кратчайшее расстояние от точки до линии действия силы, создающей данный импульс.
(Импульс- произведение скорости точки на массу)
(11)
P- равнодействующая внешних сил, действующих на частицу
ro- расстояние от линии действия силы до оси вращения.
Выражение 
называется моментом равнодействующих внешних сил относительно оси вращения. 
Для установившегося движения 
Тогда выражение момента М сводится к виду:
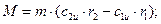(12)
Полученное уравнение называется уравнением Эйлера для вращательного движения и широко используется при изучении особенностей движения газа в лопаточных аппаратах.
Например, рассмотрим движение потока газа в центробежном компрессоре.
Величина момента (М), окружная скорость (ω) определяют теоретическую мощность:
C учетом того,что: 
С учетом (12) теоретическая мощность определится как:
(13)
Отношение Ne/m- называется теоретическим напором (Ht), развиваемым рабочим колесом компрессора:
Тогда 
Используя теорему косинусов:
Уравнение (13) превращается в вид:
(13)
Лекция 3
|
|
|
