 |
Уравнения сохранения энергии
|
|
|
|
В соответствии с первым началом термодинамики (закону сохранения энергии)
Составим баланс энергии в неподвижной системе координат, для одной и той же массы газа, заполняющей объем 1’-2’, а затем 1-2. Перемещение любого вида энергии равно разности количества данного вида энергии в положении 1-2 и 1’-2’.
Пусть на участке газа 1-2 подводится теплота q. В соответствии с 1 началом термодинамики:
, (1) где Δu- изменение внутренней энергии
l- работа расширения потока газа
Работа расширения газа может быть представлена в виде слагаемых:
- l пр- работа, затрачиваемая на проталкивание частицы газа на расстояние dx.
- l кин- работа, затрачиваемая на изменение кинетической энергии
- l пот- работа, затрачиваемая на изменение потенциальной энергии
- l тех- работа, затрачиваемая на совершение технически полезного эффекта (работа)
- l тр- работа сил трения.
Таким образом, с учетом названных составляющих работы расширения (1) можно записать в виде:
(2)
Определим составляющие для l:
- Работа проталкивания равна разнице работ по вталкиванию и выталкиванию частицы газа:
Очевидно, что работа вталкивания определится как:
Работа выталкивания:
C учетом того, что V1=F1.Δx1; V2=F2.Δx2Δx2, 
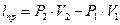(3)
Cоответственно для 1 кг газа:
(4)
(5)
После подстановки (3), (4), (5) в (2) получим:
(6)
Дальнейшее преобразование полученного выражения (6) связано с тем, что 
, подведенная извне величина q может быть представлена как:
, где qнар- наружный подвод тепла через боковую поверхность потока газа
qвнутр- внутренний подвод тепла к частице газа за счет преобразования в теплоту работы трения.
Т.е: 
Cоответственно, (6) превращается:
(7)
Из курса термодинамики известно, что энтальпия i (дж/кг) может быть определена:
|
|
|
Тогда (7) можно записать в виде:
(8) При условии отсутствия теплообмена потока газа (qнар=0)
Технической работы (l тех=0) уравнение (8) можно записать в виде:
(9)
Из (9) видно, что изменение теплосодержания в потоке теплоизолированного газа (адиабатное течение S=const) связано только с изменением скорости потока.
Если изменение скорости потока (с1 и с2) в условиях отсутствия теплообмена (qнар=0) можно пренебречь уравнение (8) можно записать:
Т.е. при адиабатном расширении потока газа техническая работа совершается за счет уменьшения величины энтальпии.
Величина 
называется располагаемым теплоперепадом
При условиях: (c1=c2), lтех=0 уравнение (8):
(9)- данное уравнение при изучении потоков газа в теплообменных аппаратах.
2. Уравнение сохранения энергии в механической форме
Запишем уравнение (1) в следующем виде:
(10)
Учитывая, что 
Выражение (10): 
(11)
Т.к. 
, то (11) перепишем в виде:
(12)
Запишем уравнение (8) в дифферинциальной форме:
(13)
Приравняв (12) и (13), получим:
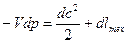(14)
После интегрирования (14) получим:
(15)- обобщенное уравнение Бернулли в механической форме:
- располагаемая работа газа, которая может быть израсходована на изменение кинетической энергии газа и на совершение технической работы.
При отсутствии технической работы (lтех=0) (15) запишем в виде:
(16)
Интеграл 
можно вычислить при условии определенности уравнений:
Если плотность газа постоянна (ρ=const),
Запишем (16) в виде:
(17)
Приведем (17) к виду:
Или 
(18)
3. Параметры заторможенного потока
В условиях отсутствия теплообмена (q=0) уравнение (9)
Перепишем в виде:
(19)
Из (19) видно:
При с1=0- i1=max; При с2=0- i2=max; Разделив (19) на сp, приняв с2=0- (остановленный поток газа), получим:
(20) To- температура заторможенного потока газа;
- величина динамического повышения температуры потока газа при торможении
Из (18) можно получить:
|
|
|
(21)
P- статическое давление;
Po- полное давление;
- динамическое давление;
Уравнение (19) можно преобразовать, учитывая, что:
к виду:
(22)
Лекция 4
Скорость распространения слабых возмущений
Скорость звука
Если газ движется с некоторыми скоростями, параметрами и и в каком- либо месте потока возникает препятствие, то оно оказывает воздействие на все частицы, находящиеся вблизи него.
Данное воздействие (возмущение) передается параметрам соседних частиц газа и распространяется на все более удаленные от препятствия участки потока.
Т.к. газ является сжимаемой средой, то возмущение передается не мгновенно, а с некоторой конечной скоростью, которая зависит от силы возмущения и от упругих свойств газа (сжимаемости).
Возмущение приводит к местному изменению давления, одноврменно с которым изменяются все параметры газа (температура, плотность и др.).
Возмущение называется слабым, если изменение параметров из за воздействия возмущения значительно меньше относительно абсолютных параметров:
(1)
В газодинамике скорость распространения любых малых возмущений в физической газовой среде называется скоростью звука (a – (м/c2)):
Согласно понятию слабых возмущений и, используя законы сохранения энергеии
для потока газа, можно вывести и записать:
(2)
(
Правая часть данного уравнения представляет собой отношение приращения давления к приращению плотности потока газа в условиях воздействия возмущений.
Плотность газа в потоке зависит от давления, температуры, но, т.к. скорость возмущений в потоке достаточно велика, то влияние теплообмена в потоке практически не учитывается.
Кроме того, вследствие небольших амплитуд смещения частиц газа при слабом возмущении трение между частицами ничтожно мало и не приводит к выделению теплоты.
Таким образом, для оценки выражения 
можно использовать уравнение адиабаты:
, откуда 
(3)
Продифферинцировав (3) по ρ, можно получить:
(4)
Из (4) получим:
Или:, с учетом 
(5)
Полученное уравнение показывает, что скорость звука является мерой сжимаемости газа. Большие значения а говорят о том, что требуются большие значения сжимаемости dp, чтобы вызвать некоторое изменение dρ. И, наоборот, если создать одинаковое dp, то при больей скорости звука они вызовут меньшие значения изменения плотности газа. Т.е. чем больше скорость звука, тем меньше сжимаемость.
|
|
|
Из (5) также следует, что скорость звука возрастает при увеличении температуры газа, а, следовательно при этом сжимаемость газа уменьшается.
Введем в рассмотрение критерий оценки скорости газовых потоков- число Маха.
Число М- отношение скорости потока к скорости звука.
(6)
В случае M<1- дозвуковой поток;
M>1- cверхзвуковой поток;
M≈1- околозвуковой поток.
В случае изучение особенностей сжимания потока пи движении газа полное давление не является простой суммой статического и динамического давления.
Для таких потоков целесообразно использовать следующие зависимости:
(7)
Разделив (7) на Т, учитывая, что и с использованием (6) получим:
(8)
Аналогичным образом для давления заторможенного потока (полное изоэнтропическое торможение) получим:
(9)
Для плотности газового потока:
(10)
Если применить уравнение сохранения энергии для потока газа, в котором p=0, можно получить:
(11)
При движении потока со скорость с= сmax вся тепловая энергия преобразуется в
Энергию направленного движения, что соответствует истечению газа в пустоту.
(Т=0, p=0). Очевидно, что 0<c<cmax.
В частном случае при с=a=cкр скорость звука называется критической скоростью
При этом все параметры состояния в данном месте потока (Т, p,ρ) также называют критическими:
(12)
Для нахождения значения Ткр в уравнении (12) воспользуемся (9) с учетом того, что М=1.
(13)
Тогда: 
(14)
Для определения p кр воспользуемся соотношением:
(15)
Или:
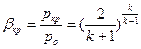(16)
|
|
|
