Условие отрыва пограничного слоя

Поскоку п.с. очень тонкий, то из основного уравнения для вязкого сжимаемого газа (уравнение Навье- Стокса) после преобразований выводится зависимость:

при y<δ

Т.е. в пределах п.с. статическое давление потока по нормали не меняется- то распределение давлений на внешней границе п.с. и на поверхности обтекаемого профиля совпадают.

Уравнение позволяет объяснение отрыва п.с.

Рассмотрим обтекание некоторой криволинейной поверхности АВ, предполагая, что давление внешнего потока вдоль данной поверхности вначале уменьшается до минимального значения в точке М и далее увеличивается.

 

 

P(x)

 

U=Uo

 

 

 

M B

A S

x

Участок внешнего потока, в котором градиент давления отрицателен, называется конфузорным. Участок внешнего потока, в котором градиент давления положителен, называется диффузорным.

На конфузорном участке поток разгоняется, на диффузорным- замедляется. Толщина п.с. на конфузорном участке уменьшается, на диффузорном- увеличивается.

За счет обмена частицами между ядром потока и п.с. на конфузорном участке АМ запас кинетической энергии в п.с. достаточно для преодоления сил трения с поверхностью. На диффузорном участке кинетическая энергия ядра потока уменьшается и, следовательно, и кинетическая энергия в п.с. В точке S запас кинетической энергии недостаточен для преодоления сил трения,, наблюдается отрыв потока, остановка п.с., обратное движение. Это приводит к резкому увеличению толщины п.с. (возникае явление набухания п.с.), резко увеличиваются потери энергии. На практике явление отрыва п.с. наблюдаются в компрессорных конфузорных и диффузорных решетках.

 

Интегральное соотношение для пограничного слоя

 

Y C

 

 

A

P

τ_o

dy

B D

dx

 

Применим уравнение импульсов (количества движения) к объему газа, заключенному между двумя параллельными сечениями АВ и CD пограничного слоя (ширина слоя =1.

В сечении АВ действует давление Р, в сечении CD-

Определим изменение количества движения для выделенного объема, учитывая, что в выделенный объем газ попадает через сечение АВ и через сечение АС.

Секундный расход газа через выделенные сечения:

, где m- масса газа, вошедшая через АВ

- масса газа, вошедшая через АС.

u- скорость потока в приграничном слое.

Суммарный расход газа составит:

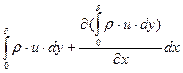
Количество движения через сечение АВ:

Количество движения через сечение АС:

u_o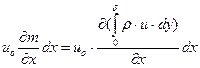

Соответственно, изменение количества движения объема газа за счет поступления частиц через сечения АВ и АС составит:

 

u₀- cкорость внешнего потока газа (ядра).

Изменение количества движения через сечение СD:

Изменение количества движения для выделенного объема АВСD:

Равно проекции на ось x импульсов действующих сил:

- давления газа на сечения АВ и СD;

- cилы трения на участке ВD;

Проекции сил давления на ось x найдем как:

Пренебрегая бесконечно малыми величинами второго порядка можно получить выражение:

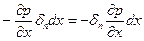
Единичное изменение силы трения определится как:

Приравняв секундное изменение количества движения к импульсу сил и переходя к полным производным, получим:

Лекция 8

Элементы газовой динамики единичного профиля и решетки профилей

1. Основные геометрические параметры крылевого профиля и решетки профилей

Сверхзвуковой профиль имеет острую клиновидную переднюю форму. В ряде случаев контур такого профиля составляется из прямолинейных отрезков.

Ромбовидный

 

 

Чечевицеобразный

 

Для дозвукового профиля характерны округленная передняя кромка и заостренная задняя кромка.

 

cmax

fmax

Xf

b

Xc

ε

X1

X2

 

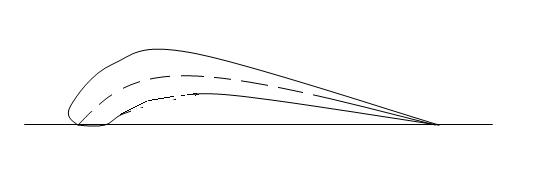
Любой профиль может получен путем изгиба симметричного профиля.

Средней линией профиля называется лини, проходящая через центр окружностей, вписанных в профиль.

Хорда профиля (b)- отрезок прямой, соединяющий две самые удаленные точки осевой дуги профиля.

Координаты точек профиля задаются обычно в долях длины хорды и которая принимается за ось абцисс, либо в мм.

Оносительной толщиной профиля называется отношение максимальной толщины на длину хорды:

Относительной выпуклостью (кривизной)- отношение максимальной стрелы прогиба осевой дуги f_max к длине хорды:

Положение м аксимальной толщины и максимальной стрелы прогиба средней линии определяются:

Кривизна профиля может характеризоваться углом изгиба средней линии ε- углом между касательной к средней линии в носике и задней кромке, называющимися соответственно- передней и задней касательными профиля.

Угол между передней касательной профиля и его хордой определяется углом X₁, между задней касательной и хордой- углом X₂.

Таким образом, можно записать:

Выбрав определенный вид осевой дужки (средней линии) и форму исходного симметричного профиля можно получить серии профилей с непрерывным изменением относительных выпуклостей и толщины.

Если рассечь рабочее колесо и направляющий аппарат осевой турбомашины цилиндрическим сечением на некотором диаметре D, а для центробежного компрессора сечением, перпендикулярным оси его вращения, то получается т.называемая кольцевая или круговая решетки соответственно.

 

Развернув цилиндрические сечения на плоскость, получим плоскую решетку профилей- т.е. совокупность бесконечного числа одинаково расположенных идентичных кривых профилей, находящихся друг от друга на одном и том расстоянии.

Линия, соединяющая соответственные точки профилей, называется фронтом решетки, а нормаль к ней- осью решетки.

 

iβ1Т

W₁

υ W2

t

β1Т

β2Т W2

β2Т

β1Т

 

Шаг решетки (t)- расстояние между двумя соседними прфилями, отчитываемыми в направлении фронта (ось u)

υ- Угол между хордой профиля и фронтом решетки называется углом установки

Отношение шага к хорде профиля называется относительным шагом решетки

Величина, обратная относительного шага решетки называется густотой решетки:

Геометрическими углами входа и выхода из решетки называются углы β_1Т, β_2T- между передней и задней касательными и фронтом решетки.

Углом атаки i- называется угол между вектором входной скорости W₁ и передней касательной

Угол отставания потока υ называется угол между задней касательной и вектором выходной скорости W₂.

Углы β₁ и β₂ называются углами входа и выхода потока в решетку соответственно.

Разность этих углов определяет поворот потока в решетке:

В газодинамике различают прямую и обратную задачи об обтекании профиля и решетки профилей.

Прямая задача- нахождении распределения давления по поверхности данного профиля при заданном времени перед профилем поля скоростей.

Обратная задача- нахождении геометрии профиля, обеспечивающего заданное распределение давления по его поверхности.

В аэродинамике решетки профилей обе эти задачи обычно рассматриваются применительно к суммарным параметрам решетки.

Под прямой задачей понимается определение аэродинамических сил и нахождение угла выхода потока при заданном поле скоростей перед решеткой заданной конфигурации. В случае потока вязкого газа определить потери полного давления.

Под обратной задачей понимается нахождение конфигурации решетки, которая поворачивает поток на заданный угол Δβ. Существует большое множество решеток, удовлетворяющих поставленным условиям. Для потенциального потока задается геометрия решетки или распределении давлений по профилю. Для вязкого газа находится оптимальная решетка (с минимальными потерями).

 

Теорема Жуковского о силовом воздействии потенциального потока на решетку профилей

Рассмотрим обтекание прямолинейной бесконечной решетки Крыловых профилей установившимся потоком газа. Полагаем, что профили имеют бесконечный размах, течение потока- плоско- параллельное. Определим силу, с которой воздействует поток на крыло единичной длины.

а₁, а₂, b₁, b₂- конгруэтные линии тока.

Принимаем к выделенному объему потока уравнение количества движения и получаем выражение для проекции на фронт равнодействующей всех сил, приложенных к объему

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: