 |
Мгновенная частота и ее статистические характеристики
|
|
|
|
Как уже отмечалось, одной из важнейших характеристик сформированного радиосигнала является стабильность его несущей частоты, требования к которой постоянно повышаются. Следует подчеркнуть, что именно стабильность частоты во многом определяет точностные характеристики, разрешающую способность и другие качественные показатели радиотехнических систем различного назначения, играет определяющую роль в решении вопросов обеспечения электромагнитной совместимости радиоэлектронных средств. Типовые ограничения на относительную нестабильность частоты в современных радиопередатчиках лежат в пределах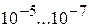 
. В специальных случаях нестабильность не должна превышать 
.
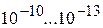Частота высокочастотных электромагнитных колебаний, используемых для формирования радиосигнала, определяется задающим генератором (возбудителем), а ее нестабильность невозможно устранить в последующих каскадах устройства. Поэтому жесткие нормы, предъявляемые к стабильности частоты, должны быть выдержаны именно в возбудителе.
При рассмотрении генераторов немодулированных гармонических колебаний, которые в дальнейшем будем называть просто автогенераторами (АГ), обычно предполагается, что их выходное напряжение имеет чисто синусоидальную форму. Спектр такого колебания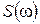 
, часто называемого монохроматическим, представляет собой одиночную спектральную линию. Однако монохроматическое колебание является идеализированной моделью реального выходного сигнала, позволяющей сравнительно просто решить ряд вопросов, связанных в основном с энергетикой процессов в АГ.
Реальное напряжение на выходе АГ не является монохроматическим хотя бы по тому, что оно существует только на ограниченном интервале времени, а потому не может иметь спектр в виде одиночной линии. Однако главным образом это обусловлено тем, что параметры и режим работы АГ зависят от большого числа внешних факторов, изменяющихся во времени. Кроме того, в реальных АГ всегда действуют флуктуационные возмущения –естественные спутники любого физического процесса. Все это приводит к изменению параметров генерируемых колебаний, в результате чего они становятся случайными функциями времени.
|
|
|
Тем не менее, сигналы на выходе АГ являются узкополосными процессами, т. е. их энергия сосредоточена в узкой полосе частот, ширина которой значительно меньше средней частоты колебаний. Это позволяет представить их в виде гармонических колебаний с медленно изменяющимися амплитудой и начальной фазой:
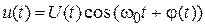, (1.1)
где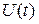 
= 
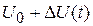– мгновенная амплитуда колебания, имеющая среднее значение 
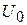, не зависящее от времени; 
<< 
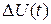– отклонение амплитуды от среднего значения.
Полная текущая фаза колебания (аргумент косинуса в (1.1))
Ф(t) =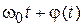 
. (1.2)
Мгновенная частота колебания определяется следующим образом:
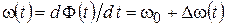, (1.3)
где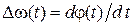 
– отклонение мгновенного значения частоты от ее среднего значения 
.
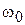Согласно формулам (1.2) и (1.3) среднюю частоту следует определить как
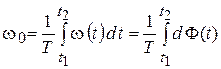, (1.4)
где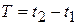 
– интервал наблюдения (или существования) колебаний.
Медленность изменени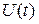й и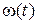 
в выражении (1.1) понимается в том смысле, что заметные изменения этих параметров происходят за время, существенно превышающее средний период колебаний 
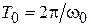. Действи-тельно, если 
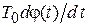<< 2 
, то 
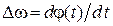<< 2 / 
.
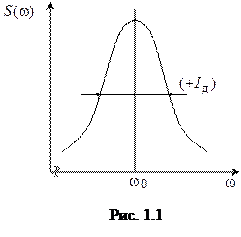Таким образом, выходное напряжение АГ представляет собой гармоническое колебание, модулированное по амплитуде и фазе (следовательно, и по частоте), и имеет энергетический спектр 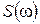не в виде одиночной линии, а в виде «контура» (рис. 1.1) со средней шириной 
. Под обычно понимают ширину «контура» на уровне 0.5 от максимального значения 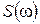. Поэтому часто говорят об «уширении» спектральной линии, а само колебание называют квазигармоническим.
|
|
|
Энергетический спектр квазигармонического колебания может служить мерой его нестабильности в широком смысле, т. е. мерой его отличия от идеального гармонического колебания. Различить влияние амплитудных и фазовых (частотных) флуктуаций по виду энергетического спектра высокочастотных колебаний практически невозможно.
Поскольку случайный характер процессов 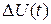и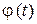 
и их влияние на работу конкретной радиотехнической системы могут быть различными, более корректно рассмотреть статистические и спектральные характеристики раздельно амплитудных и, особенно, фазовых флуктуаций вблизи несущей частоты. Более того, в большинстве случаев малые и медленные изменения амплитуды не оказывают заметного влияния на характеристики радиосистем. Так, при амплитудной модуляции (манипуляции) полезный модулирующий сигнал вызывает значительно большие изменения амплитуды, так что влиянием 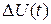можно пренебречь. При частотной или фазовой модуляциии амплитуда колебаний вообще не несет информации, а при приеме таких сигналов они подвергаются глубокому амплитудному ограничению, поэтому в дальнейшем влияние 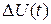рассматриваться не будет.
При неизменной амплитуде реального гармонического колебания его нестабильность также можно описать энергетическим спектром и уширением спектральной линии. Однако с практической точки зрения нестабильность колебания часто целесообразно характеризовать нестабильностью его частоты и фазы, поскольку последние проще измерить. Более того, нестабильность этих параметров во многих случаях непосредственно связана с основными показателями конкретной радиосистемы. В связи с этим первоначально рассмотрим статистические характеристик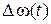и 
и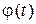 
.
Поскольку 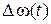и 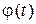в общем случае являются случайными функциями времени, можно говорить лишь о вероятности того или иного их значения.
В соответствии со сказанным,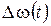 
можно рассматривать как случайный процесс, в первом приближении удовлетворяющей условиям стационарности и эргодичности 
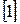. Для его описания обычно используют такие статистические характеристики, как автокорреляционная функция
|
|
|
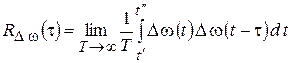, (1.5)
где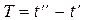 
– время существования колебаний, и спектральная плотность мощности мгновенного отклонения частоты
,
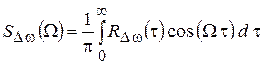связанные друг с другом прямым и обратным преобразованиями Фурье ,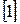
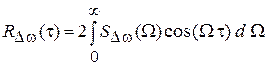. (1.6)
Отметим, что в соответствии с (1.3) и (1.4) среднее значение 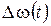= 0.
Важнейшим физическим свойством автокорреляционной функции и энергетического спектра является то, что они описывают как «интенсивность», так и «быстроту» отклонения 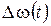относительно нулевого уровня и являются в этом смысле универсальными характеристиками нестабильности частоты.
Дисперсия функции 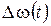, характеризующая «интенсивность» отклонения частоты, связана с автокорреляционной функцией и энергетическим спектром соотношениями
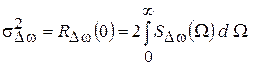. (1.7)
Дисперсия мгновенного отклонения частоты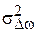 
характеризует процесс изменения частоты относительно среднего значения односторонне, никак не отражая того, как быстро происходят эти изменения, в то время, как во многих случаях это важно. Поэтому более полными характеристиками являются 
и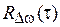 
.
В некоторых случаях удобней пользоваться функцией спектральной плотности мощности флуктуаций фазы 
= 
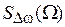. (1.8)
Соотношение (1.8) вытекает из того, что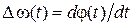 
, а дифференцированию во «временной области» (если речь идет об энергетических спектрах) соответствует умножение на в «частотной области». Величина измеряется в децибелах среднего квадрата фазовых отклонений от опорного колебания по отношению к 1 рад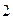 
в полосе 1 Гц для каждого значения частоты отстройки (
).
|
|
|
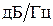