 |
Влияние нестабильности частоты на характеристики радиотехнических устройств и систем
|
|
|
|
Одной из причин, оправдывающих целесообразность введения понятий кратковременной и долговременной нестабильностей частоты, является их различное влияние на работу той или иной радиосистемы. Рассмотрим этот вопрос более подробно.
В первую очередь обратимся к системе радиосвязи, использующей сигналы с амплитудной модуляцией. Как известно, обработка амплитудно-модулированного (АМ) сигнала в простейшем случае сводится к его фильтрации в трактах высокой и промежуточной частоты и последующему амплитудному детектированию.
Введем понятие результирующей амплитудно-частотной характеристики коэффициента передачи (усиления) 
каскадов приемника, осуществляющих фильтрацию. Под 
будем понимать расстройку относительно средней частоты полосы пропускания фильтров усилителя промежуточной частоты (УПЧ), вызванную нестабильностями частот возбудителя передатчика и гетеродина приемника. Естественно, что при отсутствии нестабильности = 0, а принимает максимальное значение, равное 
.
 |
Медленные изменения несущей частоты и частоты гетеродина (или одной из них), обусловленные долговременной нестабильностью, вызывают соответствующие изменения
и 
. Поскольку инерционными свойствами фильтрующих каскадов приемника в этом случае можно пренебречь, медленные изменения 
будут приводить к «медленной» паразитной амплитудной модуляции сигнала на входе детектора, что и иллюстрирует рис. 1.4.
Для того чтобы глубина этой паразитной модуляции была существенно меньше полезной необходимо, чтобы изменения частоты за счет нестабильности были значительно меньше полосы пропускания результирующей частотной характеристики приемника – 
(рис. 1.4). В свою очередь 
выбирается близкой к ширине спектра АМ сигнала – 
. Таким образом, для систем связи с амплитудной модуляцией абсолютная долговременная нестабильность должна быть значительно меньше ширины спектра АМ сигнала
|
|
|
<< . (1.16)
Для оценки влияния быстрых изменений , вызванных кратковременной нестабильностью, целесообразно воспользоваться представлением рассматриваемых процессов в частотной области (рис. 1.5), где изображены амплитудно-частотная характеристика и спектр сигнала на входе УПЧ. Быстрым изменениям соответствуют спектральные составляющие, лежащие за пределами полосы пропускания селективных цепей и эффективно подавляемые ими. Во временной области это означает, что инерционные свойства фильтров приемника препятствуют быстрым изменениям амплитуды проходящего сигнала.
Следовательно, в системах связи с АМ-сигналами требования к кратковременной нестабильности частоты будут менее жесткими, чем к долговременной.
Рассмотрим теперь систему связи с частотной модуляцией (ЧМ). Обработка сигнала в ЧМ-приемнике обычно сводится к фильтрации и частотному детектированию. Избирательные свойства, как и при АМ, приводят к появлению паразитной амплитудной модуляции при медленных изменениях . Поэтому для пренебрежимо малой паразитной АМ необходимо выполнить условие, аналогичное (1.16), т. е. << 
. Однако ширина спектра ЧМ-сигнала существенно больше ширины спектра АМ-сигнала. Кроме того, в ЧМ-приемниках, как правило, используется система автоматической подстройки частоты, как раз и устраняющая медленные изменения . Помимо этого сигнал промежуточной частоты может быть подвергнут глубокому амплитудному ограничению. Все сказанное говорит о том, что требования к абсолютной долговременной нестабильности частоты при ЧМ существенно менее жесткие, чем при АМ.
Быстрые изменения частоты воспринимаются как полезный сигнал и тем самым искажают последний, поэтому кратковременная нестабильность частоты при ЧМ играет важную роль. Для того чтобы нестабильность не приводила к нежелательным искажениям, необходимо выполнить условие
|
|
|
<< 
, (1.17)
где – среднеквадратическое значение полезной девиации частоты ЧМ-сигнала.
В системах передачи информации на одной боковой полосе (ОБП) оказываются важными как долговременная, так и кратковременная нестабильности частоты. Обработка сигнала в системах с ОБП сводится к фильтрации и последующему переносу спектра ОБП в область нулевой частоты. Последняя операция осуществляется в приемнике с помощью преобразователя частоты и (в системах с подавленной несущей) независимого местного гетеродина.
Если за счет долговременной нестабильности несущей частоты передатчика и частоты гетеродина промежуточная частота изменяется на , то спектры переданного сигнала 
и сигнала, восстановленного в приемнике 
, оказываются сдвинутыми друг относительно друга по частоте на эту величину. При этом переданный и принятый сигналы будут различными и во временной области. Экспериментальные исследования показывают, что для сохранения натуральности речи необходимо выполнить условие [5]
≤ 50 Гц, (1.18)
а для обеспечения высокохудожественной передачи речи или музыки ≤ 10 Гц. При ≥ 300 Гц пропадает разборчивость речи. Из сравнения (1.18) с (1.16) следует, что требования к долговременной нестабильности частоты при ОБП существенно выше, чем при АМ. Для снижения этих требований в ряде случаев передают не только ОБП, но и подавленный до определенного уровня сигнал несущей частоты (пилот-сигнал), используемый для автоподстройки гетеродина приемника.
Для оценки влияния быстрых изменений частоты на работу систем с ОБП напомним, что радиосигнал на ОБП представляет собой сигнал с комбинированной (амплитудной и частотной (фазовой)) модуляцией 
и может быть представлен в виде 
, где 
– изменение мгновенной фазы за счет модуляции.
При идеальном приеме на выходе приемника будет восстановлен переданный сигнал 
. Однако за счет нестабильности частот несущей и местного гетеродина при переносе в область нулевой частоты сигнал искажается и принимает вид 
= 
, где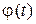 
– изменяющаяся за счет нестабильности составляющая мгновенной фазы.
|
|
|
Последнее выражение можно представить в виде
= 
,
где 
– среднее значение частоты передаваемого информационного сигнала 
; 
– уклонение мгновенного значения частот несущей и гетеродина; 
– быстро изменяющаяся функция, содержащая часть информации о передаваемом сигнале.
Для того чтобы быстрые изменения частоты, обусловленные кратковременной нестабильностью, не искажали передаваемый сигнал, необходимо выполнение условия << 
, где – среднеквадратическое значение функции . Как правило, существенно меньше, чем при обычной ЧМ. Поэтому требования к кратковременной нестабильности для систем передачи на ОБП более жесткие, чем при ЧМ.
Еще более жесткие требования к кратковременной и долговременной нестабильностям предъявляются к многоканальным системам с ОБП.
Обратимся теперь к радиолокационным системам (РЛС). Рассмотрим влияние нестабильности частоты на точность измерения дальности радиолокатором, работающем на основе фазового метода 
. Будем считать, что передатчик РЛС излучает непрерывный квазигармонический сигнал с постоянной амплитудой 
= 
. Разность полных фаз между отраженным от цели сигналом и опорным сигналом в устройстве сравнения РЛС составит
= 
– 
= 
, (1.19)
где 
– время прохождения сигнала до цели и обратно, эквивалентное в данном случае времени усреднения; 
.
Используя соотношение (1.19), нетрудно определить дальность до цели:
+ 
, (1.20)
где 
– усредненная за время наблюдения частота зондирующего сигнала; с – скорость света; – истинная дальность до цели; – ошибка по дальности.
Как известно , простейшим вариантам фазовых РЛС свойственна неоднозначность определения дальности за счет того, что измерители регистрируют изменение фаз в пределах от 0 до 2π. В нашем случае будем считать, что в РЛС предусмотрена возможность измерения грубой дальности, устраняющего неоднозначность.
Нетрудно заметить, что флуктуации начальной фазы – 
приводят к появлению ошибки по дальности. Для оценки погрешности целесообразно ввести относительную среднеквадратическую ошибку 
, определяемую следующим образом:
|
|
|
= 
= 
, (1.21)
где 
; 
.
Сравнивая (1.21) с (1.12) и учитывая (1.13), нетрудно убедиться, что среднеквадратическая ошибка по дальности может быть сведена к виду
= 
= 
.
Таким образом, согласно (1.13) и (1.21) относительная среднеквадратическая ошибка определения дальности равна относительной кратковременной нестабильности частоты.
Для определения скорости движения цели в РЛС широко используется эффект Допплера , который заключается в изменении частоты сигналов, отраженных от движущихся целей. Разность частот зондирующего и отраженного сигналов 
, называемая допплеровской частотой, определяется соотношением 
= 
, где – частота зондирующего сигнала; 
– радиальная составляющая скорости движения цели по отношению к РЛС.
Считая, как и ранее, что РЛС излучает квазигармонический сигнал с постоянной амплитудой 
= , для разности полных фаз между отраженным от цели сигналом и опорным сигналом в устройстве сравнения РЛС можно получить следующее соотношение
= – = 
– 
, (1.22)
где .
Продифференцировав по времени (1.22), для случая отсутствия нестабильности ( 0) получим 
= 
. В реальной ситуации за счет нестабильности частоты 
≠ 0, следовательно
, (1.23)
где 
– допплеровская частота, полученная в результате измерения; 
= 
– ошибка измерения.
Согласно (1.23), абсолютная среднеквадратическая ошибка измерения частоты Допплера может быть найдена следующим образом:
= 
, (1.24)
где 
.
Последняя формула может быть подвергнута преобразованиям, аналогичным (1.12), (1.13). Если при этом учесть, что энергетический спектр производной от функции равен энергетическому спектру самой функции, умноженному на квадрат частоты анализа, то выражение (1.24) можно привести к виду
= 2 
.
Таким образом, среднеквадратическая ошибка измерения скорости 
= = 
определяется временем 
(т. е. фактически дальностью до цели) и энергетическим спектром флуктуаций частоты 
. Последний, как было показано ранее, является характеристикой кратковременной нестабильности.
Помимо измерения скорости цели допплеровское смещение частоты ши-роко используется в спутниковых радионавигационных системах (РНС) для определения координат наземных объектов . Остановимся более подробно на методе определения координат, основанном на интегрировании допплеровской частоты.
Пусть в точке приема вычисляется интеграл
= 
= 
, (1.25)
где 
– фиксированный интервал времени; 
– радиальная скорость искусственного спутника Земли (ИСЗ) относительно потребителя.
Как следует из формулы (1.25),
|
|
|
= 
. (1.26)
Таким образом, интеграл от допплеровской частоты в пределах фиксирует разность дальностей до ИСЗ в последовательные моменты времен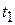и 
и 
, т. е. дает значение навигационного параметра в разностно-дально-мерной РНС с опорными станциями, координаты которых определяются положениями ИСЗ в эти моменты времени.
Фиксированное значение 
соответствует поверхности положения в виде гиперболоида, а его пересечение с поверхностью Земли дает линию положения. Произведя интегрирование в течение интервала времени 
, найдем вторую разность расстояний и получим вторую линию положения. Положение наблюдателя характеризуется точками пересечения линий положения, а получающаяся неоднозначность устраняется с помощью априорных данных о координатах потребителя. Естественно, что ошибки в определении допплеровской частоты приводят к появлению соответствующей ошибки и в найденных координатах потребителя.
Описанный метод определения координат, называемый интегральным допплеровским, используется, например, в низкоорбитальной спутниковой РНС «Транзит». В этой системе каждый ИСЗ находится в зоне радиовидимости от 10 до 16 мин, а период передачи навигационной информации равен 2 мин . Следовательно, за один пролет ИСЗ можно получить 5…8 линий положения. Избыточное их число используется для статистического сглаживания получаемых оценок координат. Подчеркнем, что в данном случае время усреднения составляет 2 мин, т. е. речь идет о влиянии средневременной нестабильности частоты на погрешность измерения.
Основные характеристики РЛС с селекцией движущихся целей по скорости (СДЦ) (разрешающая способность по скорости и дальность действия) зависят от уширения спектральной линии самого зондирующего сигнала и интенсивности его спектральных компонент на «крыльях» спектра 
.
Приемное устройство РЛС с СДЦ содержит совокупность настроенных на различные частоты узкополосных фильтров, выходные сигналы которых соответствуют целям, движущимся с различными скоростями. В идеальном случае разрешающая способность по скорости, т. е. минимальная разница между частотами отраженных от целей сигналов за счет допплеровского сдвига, определяется полосой пропускания и стабильностью характеристик фильтров.
Реально за счет нестабильности зондирующего сигнала его спектр расширяется и «крылья» спектра более мощного отраженного сигнала могут иметь большую интенсивность, чем спектральные компоненты сигналов, отраженных от целей, движущихся с близкими скоростями, но находящихся на большем расстоянии или имеющих меньшую эффективную площадь рассеяния. На рис. 1.6, а и б представлены идеальные (вертикальные линии) и реальные спектры соответственно зондирующего и отраженных сигналов.
Сказанное приводит к частичному или полному перекрытию спектров. Нетрудно заметить, что уширение спектральной линии самого зондирующего сигнала и интенсивность его спектральных компонент на «крыльях» спектра приводит к частичному или полному перекрытию спектров и к ухудшению разрешающей способности по скорости и уменьшению дальности действия РЛС с СДЦ.
СИНТЕЗАТОРЫ ЧАСТОТЫ
|
|
|
