 |
Усредненная частота и ее статистические характеристики
|
|
|
|
Рассмотренные ранее характеристики нестабильности частоты целесообразно использовать на практике только в том случае, если они могут быть измерены с помощью некоторых технических средств. При этом немаловажную роль играют удобство измерений и простота измерительной аппаратуры.
Введенные характеристики нестабильности мгновенной частоты не удовлетворяют отмеченным требованиям по следующей причине. На практике измерение частоты производится резонансным и гетеродинным методами или методами дискретного счета. Последние используются наиболее часто, позволяя обеспечить более высокую точность измерений.
Электронно-счетный частотомер, работающий по этому принципу, преобразует квазигармоническое колебание в последовательность коротких импульсов, частота следования которых равна частоте измеряемого колебания. Обычно импульсы генерируются в те моменты, когда 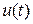 = 0. В состав частотомера входит счетчик импульсов, который с помощью специальной стробирующей схемы производит счет импульсов за время
= 0. В состав частотомера входит счетчик импульсов, который с помощью специальной стробирующей схемы производит счет импульсов за время  =
= 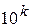 с (
с ( – целое положительное или отрицательное число, включая 0). Если за время
– целое положительное или отрицательное число, включая 0). Если за время  количество зафиксированных счетчиком импульсов оказалось равным N, то частота принимается равной
количество зафиксированных счетчиком импульсов оказалось равным N, то частота принимается равной 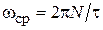 . Очевидно, что в силу дискретного характера счета числа периодов возможна потеря единицы в младшем разряде, которая и определяет погрешность измерений. Однако эту погрешность можно уменьшить в М раз, пропустив исследуемое колебание через умножитель частоты с кратностью умножения М.
. Очевидно, что в силу дискретного характера счета числа периодов возможна потеря единицы в младшем разряде, которая и определяет погрешность измерений. Однако эту погрешность можно уменьшить в М раз, пропустив исследуемое колебание через умножитель частоты с кратностью умножения М.
Если пренебречь этой погрешностью, то можно считать, что электронно-счетный частотомер измеряет набег полной фазы колебания Ф(t) за интервал времени  и делит его на
и делит его на  . Таким образом, частотомер регистрирует
. Таким образом, частотомер регистрирует
|
|
|
 , (1.9)
, (1.9)
где  – момент начала измерения, а
– момент начала измерения, а  – интервал усреднения. Поскольку
– интервал усреднения. Поскольку  на относительно небольших интервалах наблюдения – случайная функция времени,
на относительно небольших интервалах наблюдения – случайная функция времени,  также будет случайной функцией и
также будет случайной функцией и  и
и  . Из (1.2) и (1.9) нетрудно получить
. Из (1.2) и (1.9) нетрудно получить
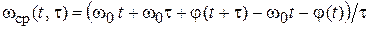 =
=  , (1.10)
, (1.10)
где
 (1.11)
(1.11)
– усредненное на интервале  уклонение частоты.
уклонение частоты.
Из соотношений (1.4), (1.9) и (1.10) вытекает, что
 ,
,
где  – интервал наблюдения (или существования) колебаний.
– интервал наблюдения (или существования) колебаний.
Таким образом,  представляет собой разность частот, усредненных на интервалах усреднения
представляет собой разность частот, усредненных на интервалах усреднения  и наблюдения
и наблюдения  .
.
На рис. 1.2 приведен пример реализации мгновенной частоты на интервале наблюдения  и показаны значения усредненных частот
и показаны значения усредненных частот  и их уклонений
и их уклонений  при различных
при различных  и времени измерения. Очевидно, что и при изменении
и времени измерения. Очевидно, что и при изменении  и при сдвиге момента начала усреднения
и при сдвиге момента начала усреднения  и
и  будут изменяться по случайному закону. Определим дисперсию усредненного уклонения частоты. Учитывая (1.11), нетрудно получить
будут изменяться по случайному закону. Определим дисперсию усредненного уклонения частоты. Учитывая (1.11), нетрудно получить
 =
=  =
=  , (1.12)
, (1.12)
 |
где
 ;
;  – время наблюдения.
– время наблюдения.
Рис. 1.2
Раскрывая квадрат под знаком интеграла и учитывая соотношения (1.5)– (1.7), записанные для мгновенной фазы, (1.8) и очевидное равенство
 , определим
, определим
 =
= 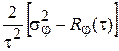 =
=  =
=
= 8  = 2
= 2 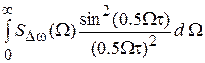 . (1.13)
. (1.13)
Последняя формула связывает дисперсию  усредненного укло-нения частоты со спектральной плотностью мощности флуктуаций мгновенной частоты. Необходимо отметить, что полученное соотношение для дисперсии справедливо только при бесконечном времени наблюдения (существования) колебаний
усредненного укло-нения частоты со спектральной плотностью мощности флуктуаций мгновенной частоты. Необходимо отметить, что полученное соотношение для дисперсии справедливо только при бесконечном времени наблюдения (существования) колебаний  , которое в реальных случаях всегда конечно.
, которое в реальных случаях всегда конечно.
Поэтому на практике используется оценка дисперсии, а конечное время наблюдения учитывается введением в подынтегральное выражение формулы (1.13) «фильтрующего» множителя [2]:
 , (1.14)
, (1.14)
исключающего из дисперсии спектральные составляющие  , лежащие на частотах
, лежащие на частотах 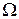 <
<  и адекватно не отраженные в спектре при малых временах наблюдения.
и адекватно не отраженные в спектре при малых временах наблюдения.
Анализ полученного выражения показывает, что в зависимости от конкретных значений  и
и  вклад различных составляющих энергетического спектра
вклад различных составляющих энергетического спектра  в величину дисперсии оказывается различным. Так, за счет наличия «фильтрующего» множителя
в величину дисперсии оказывается различным. Так, за счет наличия «фильтрующего» множителя 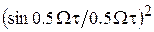 с ростом
с ростом  убывает влияние на величину оценки дисперсии высокочастотных составляющих мгновенного уклонения частоты. Уменьшение
убывает влияние на величину оценки дисперсии высокочастотных составляющих мгновенного уклонения частоты. Уменьшение 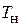 , как уже отмечалось, приводит к тому, что за счет множителя в квадратных скобках (1.14) из рассмотрения исключаются низкочастотные составляющие
, как уже отмечалось, приводит к тому, что за счет множителя в квадратных скобках (1.14) из рассмотрения исключаются низкочастотные составляющие  .
.
|
|
|
Нетрудно заметить, что при 
 , а при
, а при  и
и 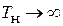
 , т. е. при увеличении интервала усреднения дисперсия усредненного уклонения частоты убывает, стремясь к нулю, а при уменьшении
, т. е. при увеличении интервала усреднения дисперсия усредненного уклонения частоты убывает, стремясь к нулю, а при уменьшении  – приближается к дисперсии мгновенного отклонения частоты.
– приближается к дисперсии мгновенного отклонения частоты.
Таким образом, в качестве весьма универсальных характеристик нестабильности частоты могут быть приняты различные статистические функции, достаточно полно описывающие процесс изменения частоты в части как интенсивности ее уклонения от среднего значения, так и скорости этих уклонений. Однако с точки зрения унификации и стандартизации терминологии, измерительной аппаратуры и самих АГ целесообразно выбрать вполне определенные характеристики. В связи с этим на международном уровне было рекомендовано принять в качестве основных характеристик функцию спектральной плотности мощности нестабильности мгновенной частоты  и дисперсию усредненного уклонения частоты
и дисперсию усредненного уклонения частоты  .
.
Это объясняется, во-первых, тем, что, зная эти характеристики, можно достаточно просто проанализировать влияние нестабильности на качественные показатели радиотехнических систем различного назначения (см. 1.4), и, во-вторых, эти характеристики просто измерить.
Выбор именно двух характеристик, а не одной (хотя они и связаны друг с другом соотношением (1.14)), обусловлен тем, что 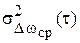 характеризует процесс изменения частоты во временной области, а
характеризует процесс изменения частоты во временной области, а  – в частотной (спектральной). Неудобство этих характеристик с практической точки зрения заключается в том, что они являются функциями, а не числами. Следует отметить, что в ряде случаев в качестве характеристики нестабильности целесообразно использовать высокочастотный спектр самого квазигармонического колебания
– в частотной (спектральной). Неудобство этих характеристик с практической точки зрения заключается в том, что они являются функциями, а не числами. Следует отметить, что в ряде случаев в качестве характеристики нестабильности целесообразно использовать высокочастотный спектр самого квазигармонического колебания 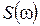 .
.
|
|
|


