 |
Пассивные цифровые синтезаторы
|
|
|
|
 |
Одна из простейших схем цифрового синтеза (схема двухуровневого синтезатора) представлена на рис. 2.1. Принцип ее работы заключается в следующем. В формирователе импульсов ФИ из гармонических колебаний ОКГ формируется периодическая последовательность коротких импульсов с частотой следования
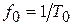 , поступающая затем на вход делителя с переменным коэффициентом деления ДПКД. Коэффициент деления ДПКД выбирается так, чтобы частота следования импульсов на выходе последнего была в два раза выше требуемой частоты сигнала на выходе синтезатора. Этот поток импульсов подается на вход триггера Т, создающего последовательность прямоугольных импульсов со скважностью 2 и частотой следования, равной заданной. В перестраиваемом полосовом фильтре ПФ из этой импульсной последовательности выделяется синусоидальный сигнал с частотой первой гармоники. Изменяя коэффициент деления ДПКД и перестраивая ПФ, можно изменять частоту выходных колебаний.
, поступающая затем на вход делителя с переменным коэффициентом деления ДПКД. Коэффициент деления ДПКД выбирается так, чтобы частота следования импульсов на выходе последнего была в два раза выше требуемой частоты сигнала на выходе синтезатора. Этот поток импульсов подается на вход триггера Т, создающего последовательность прямоугольных импульсов со скважностью 2 и частотой следования, равной заданной. В перестраиваемом полосовом фильтре ПФ из этой импульсной последовательности выделяется синусоидальный сигнал с частотой первой гармоники. Изменяя коэффициент деления ДПКД и перестраивая ПФ, можно изменять частоту выходных колебаний.
Очевидно, что в общем случае при некоторых значениях  требуемый коэффициент деления ДПКД может оказаться нецелым числом. Счетчиковые делители, на базе которых создается ДПКД, не могут поделить частоту на нецелое число, поэтому в подобных случаях поступают следующим образом. Положим, что коэффициент деления ДПКД должен быть установлен равным (
требуемый коэффициент деления ДПКД может оказаться нецелым числом. Счетчиковые делители, на базе которых создается ДПКД, не могут поделить частоту на нецелое число, поэтому в подобных случаях поступают следующим образом. Положим, что коэффициент деления ДПКД должен быть установлен равным ( ), где
), где 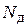 , l, m – целые числа и
, l, m – целые числа и  , т. е.
, т. е. 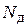 – целая часть коэффициента деления, а
– целая часть коэффициента деления, а  – его дробная часть (несократимая дробь). Для этого, например, в течение первых l циклов деления коэффициент деления ДПКД устанавливается равным
– его дробная часть (несократимая дробь). Для этого, например, в течение первых l циклов деления коэффициент деления ДПКД устанавливается равным  , а в последующих (
, а в последующих ( ) циклах – равным
) циклах – равным  . Тогда средний за m циклов коэффициент деления
. Тогда средний за m циклов коэффициент деления
 .
.
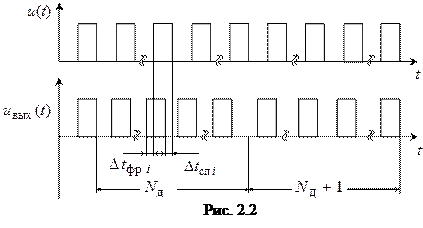
При этом сигнал на выходе синтезатора будет иметь нужную частоту, но с некоторым колебанием фазы, изменяющейся по периодическому закону с периодом  . Таким образом, в рассматриваемом случае сигнал на выходе Т-триггера представляет собой последовательность импульсов, периодически смещающихся относительно «гипотетических» импульсов, имеющих постоянную частоту следования
. Таким образом, в рассматриваемом случае сигнал на выходе Т-триггера представляет собой последовательность импульсов, периодически смещающихся относительно «гипотетических» импульсов, имеющих постоянную частоту следования  =
= 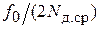 . Сказанное поясняется временными диаграммами (рис. 2.2).
. Сказанное поясняется временными диаграммами (рис. 2.2).
|
|
|
 |
Следовательно, спектр выходного сигнала будет содержать побочные составляющие. Для определения уровня максимальной из побочных составляющих, возникающих в выходном сигнале ССЧ при нецелочисленном коэффициенте деления, воспользуемся методом Я. Д. Ширмана [9]. Согласно этому методу, подобная последовательность может быть представлена в виде ряда Фурье, каждая из спектральных составляющих которого периодически изменяется во времени. Считая для простоты, что речь идет об импульсах единичной амплитуды, можно записать
 ,
,
где  – постоянная составляющая;
– постоянная составляющая;
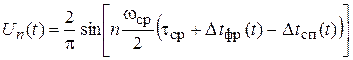
и  – амплитуда и фаза n -й гармоники соответственно;
– амплитуда и фаза n -й гармоники соответственно;  и
и  – средние частота и период повторения импульсов на выходе Т-триггера (частота и период следования идеальной «гипотетической» последовательности).
– средние частота и период повторения импульсов на выходе Т-триггера (частота и период следования идеальной «гипотетической» последовательности).
Полосовой фильтр, стоящий на выходе ССЧ, выделит из импульсной последовательности на его входе только первую гармонику, т. е.
 .
.
Поскольку для каждого из импульсов рассматриваемой последовательности закон изменения  и
и  одинаков, а
одинаков, а 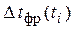 практически равно
практически равно 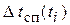 , можно утверждать, что
, можно утверждать, что 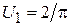 ,
,  , где
, где 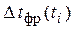 =
=  =
=  .
.
Таким образом, на выходе ССЧ будет присутствовать фазомодулированный сигнал с постоянной амплитудой и несущей частотой, равной  .
.
Графики изменения  для случаев
для случаев  и
и 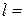 1, 2,..., 9, 10 (при этом
1, 2,..., 9, 10 (при этом  будет принимать значения
будет принимать значения 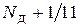 ,
,  , …,
, …,  ,
,  ) представлены на рис. 2.3, где n – номер цикла деления. Подчеркнем, что при выполнении одного цикла деления на
) представлены на рис. 2.3, где n – номер цикла деления. Подчеркнем, что при выполнении одного цикла деления на  формируемый импульс сдвигается в сторону опережения на величину
формируемый импульс сдвигается в сторону опережения на величину 
 , а при делении на (
, а при делении на (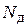 +1) – на
+1) – на  – в сторону отставания. Нетрудно убедиться, что максимальный временной сдвиг между идеальными и реальными импульсами будет наблюдаться в том случае, когда
– в сторону отставания. Нетрудно убедиться, что максимальный временной сдвиг между идеальными и реальными импульсами будет наблюдаться в том случае, когда  , а закон изменения
, а закон изменения  будет близок к треугольному. При этом
будет близок к треугольному. При этом 
 , а индекс фазовой модуляции будет равен
, а индекс фазовой модуляции будет равен
|
|
|
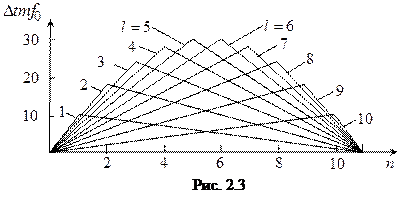
 . (2.1)
. (2.1)
 |
Поскольку  является периодической функцией времени, максимальная побочная спектральная составляющая
является периодической функцией времени, максимальная побочная спектральная составляющая 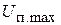 в спектре выходного сигнала ССЧ будет определяться амплитудой максимальной гармоники (в данном случае первой) при разложении
в спектре выходного сигнала ССЧ будет определяться амплитудой максимальной гармоники (в данном случае первой) при разложении  в ряд Фурье и будет равна
в ряд Фурье и будет равна
 =
= 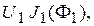
где  – функция Бесселя первого рода первого порядка;
– функция Бесселя первого рода первого порядка;
 =
=  =
= 
 (2.2)
(2.2)
– амплитуда первой гармоники при разложении  в ряд Фурье.
в ряд Фурье.
Считая, что индекс получаемой паразитной фазовой модуляции меньше единицы, и учитывая (2.2) и справедливость приближенного равенства  , окончательно получим
, окончательно получим
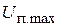 =
= 
 =
=  =
= 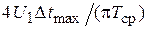 . (2.3)
. (2.3)
Относительный уровень максимальной спектральной составляющей в выходном сигнале синтезатора с учетом (2.3) будет равен
 . (2.4)
. (2.4)
Анализ соотношений (2.2)–(2.4) показывает, что снижение уровня побочных спектральных составляющих в выходном сигнале простейшего двухуровневого ССЧ требует в первую очередь увеличения  , что при заданном диапазоне частот выходного сигнала может быть достигнуто за счет соответствующего повышения тактовой частоты
, что при заданном диапазоне частот выходного сигнала может быть достигнуто за счет соответствующего повышения тактовой частоты  .
.
Кроме того, для снижения уровня побочных составляющих целесообразно чередовать циклы деления на 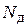 и
и  , что позволит уменьшить
, что позволит уменьшить  . Если при этом установленный коэффициент деления сохранять неизменным до тех пор, пока
. Если при этом установленный коэффициент деления сохранять неизменным до тех пор, пока 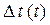 не приблизится к 0.5
не приблизится к 0.5  , а затем изменить на единицу, то выполнится неравенство
, а затем изменить на единицу, то выполнится неравенство  ≤
≤  (рис. 2.4). Закон изменения
(рис. 2.4). Закон изменения 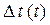 будет приближаться к пилообразному, а
будет приближаться к пилообразному, а  уменьшится и станет равным
уменьшится и станет равным
 (2.5)
(2.5)
 Выводы соотношений (2.4) и (2.5) аналогичны с той лишь разницей, что в последнем случае
Выводы соотношений (2.4) и (2.5) аналогичны с той лишь разницей, что в последнем случае  =
=  и амплитуда первой гармоники периодической последовательности пилообразных импульсов единичной амплитуды в отличие от треугольных равна
и амплитуда первой гармоники периодической последовательности пилообразных импульсов единичной амплитуды в отличие от треугольных равна  , а не
, а не  .
.
Управлять коэффициентом деления ДПКД можно с помощью счетно-решающего устройства СЧРУ, вычисляющего получаемый временной сдвиг между формируемыми и идеальными импульсами по известному отличию текущего коэффициента деления от среднего. Подобный двухуровневый синтезатор часто называют оптимальным [4]. Совокупность ДПКД и СЧРУ можно рассматривать как делитель с дробно-переменным коэффициентом деления (ДДПКД). В соответствии с соотношением (2.5) требуемую чистоту спектра выходных колебаний синтезатора можно реализовать только при больших коэффициентах деления. При этом необходимо учитывать, что максимальное значение  ограничено быстродействием существующих ДПКД.
ограничено быстродействием существующих ДПКД.
|
|
|
При введении в рассматриваемый синтезатор устройства коррекции временного положения формируемых импульсов ценой усложнения СЧРУ можно либо в n раз увеличить  , либо на
, либо на  уменьшить
уменьшить  , где n показывает, во сколько раз уменьшился временной сдвиг между идеальными и формируемыми импульсами за счет введения корректирующего устройства.
, где n показывает, во сколько раз уменьшился временной сдвиг между идеальными и формируемыми импульсами за счет введения корректирующего устройства.
Получить любую среднюю частоту и реализовать декадную установку частоты в соответствии с соотношением  (где
(где
 = 0, 1, 2, …, 9;
= 0, 1, 2, …, 9;  – минимальный десятичный разряд в значении частоты) можно сложением нескольких потоков импульсов. Вариант структурной схемы соответствующего устройства изображен на рис. 2.5 [4].
– минимальный десятичный разряд в значении частоты) можно сложением нескольких потоков импульсов. Вариант структурной схемы соответствующего устройства изображен на рис. 2.5 [4].
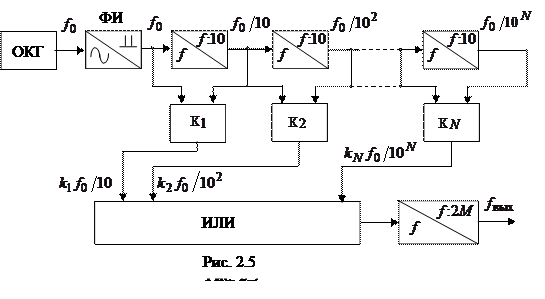 |
Исходный поток импульсов с частотой 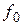 поступает последовательно на ряд делителей на 10. Управляемые ключи K1–K N имеют по два входа и по одному выходу. На входы подаются потоки импульсов со входа и выхода соответствующего делителя. Выходные импульсы каждого делителя служат метками времени, которые делят поток входных импульсов на пачки по десять в каждой. Счетчики в ключах, ориентируясь по этим меткам, ведут счет импульсов в каждой пачке и в зависимости от нужной частоты пропускают требуемое число импульсов (от одного до девяти), выбирая их так, чтобы интервалы между ними как можно меньше отличались друг от друга. Все потоки импульсов складываются на выходе схемы «ИЛИ». Если каждый ключ выделяет из десятиимпульсной пачки
поступает последовательно на ряд делителей на 10. Управляемые ключи K1–K N имеют по два входа и по одному выходу. На входы подаются потоки импульсов со входа и выхода соответствующего делителя. Выходные импульсы каждого делителя служат метками времени, которые делят поток входных импульсов на пачки по десять в каждой. Счетчики в ключах, ориентируясь по этим меткам, ведут счет импульсов в каждой пачке и в зависимости от нужной частоты пропускают требуемое число импульсов (от одного до девяти), выбирая их так, чтобы интервалы между ними как можно меньше отличались друг от друга. Все потоки импульсов складываются на выходе схемы «ИЛИ». Если каждый ключ выделяет из десятиимпульсной пачки  импульсов (
импульсов (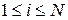 ), то за время, соответствующее периоду колебаний на выходе последнего делителя и равное
), то за время, соответствующее периоду колебаний на выходе последнего делителя и равное  , на выходе схемы «ИЛИ» появится
, на выходе схемы «ИЛИ» появится  +
+  импульсов. Следовательно, средняя частота сигнала на выходе схемы «ИЛИ»
импульсов. Следовательно, средняя частота сигнала на выходе схемы «ИЛИ»  . Включение на выходе ССЧ делителя на
. Включение на выходе ССЧ делителя на 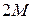 позволяет сформировать импульсы со скважностью, близкой к 2, и средней частотой
позволяет сформировать импульсы со скважностью, близкой к 2, и средней частотой  . При этом
. При этом  . Если
. Если 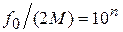 Гц, то
Гц, то  Гц, где
Гц, где  – любое целое положительное или отрицательное число включая 0.
– любое целое положительное или отрицательное число включая 0.
|
|
|
Очевидно, что, как и в предыдущем ССЧ, выходной сигнал представляет собой периодический поток импульсов с времяимпульсной модуляцией. Поэтому в спектре выходного сигнала будут присутствовать побочные спектральные составляющие, лежащие на частоте  и ее гармониках (здесь
и ее гармониках (здесь  – номер последнего по порядку ключа, на выходе которого при данной
– номер последнего по порядку ключа, на выходе которого при данной  есть поток импульсов.
есть поток импульсов.
Выбирая в каждой декаде требуемое число импульсов так, чтобы интервалы между ними наименьшим образом отличались друг от друга, для оценки относительного уровня максимальной побочной составляющей можно получить следующее соотношение  :
:

 =
=  . (2.6)
. (2.6)
Сравнивая выражения (2.5) и (2.6), нетрудно заметить, что при оптимальном построении и M = 1оба синтезатора имеют практически одинаковый уровень максимальной побочной составляющей.
Основным недостатком рассмотренных двухуровневых синтезаторов при малых  является большая кратковременная нестабильность частоты, вызванная, в общем случае, неравномерностью частоты следования выходных импульсов. Попутно отметим, что
является большая кратковременная нестабильность частоты, вызванная, в общем случае, неравномерностью частоты следования выходных импульсов. Попутно отметим, что  не зависит от коэффициента деления делителя, включенного на выходе ССЧ. Поэтому оценка уровня максимальной побочной составляющей в выходном сигнале ССЧ может быть выполнена с помощью осциллографа путем измерения отношения
не зависит от коэффициента деления делителя, включенного на выходе ССЧ. Поэтому оценка уровня максимальной побочной составляющей в выходном сигнале ССЧ может быть выполнена с помощью осциллографа путем измерения отношения  (см. (2.3)).
(см. (2.3)).
Еще один недостаток связан с тем, что при коэффициенте перекрытия  >> 2 и высоких требованиях к фильтрации высших гармоник в выходном сигнале ССЧ существенно усложняется реализация выходного полосового фильтра.
>> 2 и высоких требованиях к фильтрации высших гармоник в выходном сигнале ССЧ существенно усложняется реализация выходного полосового фильтра.
Свободны от отмеченных недостатков цифровые синтезаторы прямого синтеза (DDS – direct digital synthesizer) с потоками многоуровневых импульсов. Они обеспечивают широкие возможности формирования сигналов различной формы с различными видами модуляции и манипуляции, имеют малое время перестройки с одной частоты на другую, а уменьшение шага сетки частот (а значит, и минимальной частоты рабочего диапазона) достигается в них без особых затруднений. Однако максимальные значения рабочих частот ограничены быстродействием цифровых узлов и, как правило, не превышают 300…400 МГц.
|
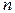 -разрядных бинарного сумматора и регистра данных, преобразователь кодов фазы в коды амплитуды ПК, обычно выполняемый на основе блока памяти кодов значений
-разрядных бинарного сумматора и регистра данных, преобразователь кодов фазы в коды амплитуды ПК, обычно выполняемый на основе блока памяти кодов значений 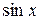 , и цифро-аналоговый преобразователь ЦАП.
, и цифро-аналоговый преобразователь ЦАП.|
|
|
 |
Особенности работы ЦВС рассмотрим на примере синтезатора, предназначенного для формирования моногармонического сигнала.
Пусть в ЧР записан код 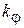 дискрета фазы
дискрета фазы  для текущего значения выходной частоты
для текущего значения выходной частоты 
 =
=  , где
, где  – число дискретов фазы (объем НКФ), n – количество разрядов кода;
– число дискретов фазы (объем НКФ), n – количество разрядов кода; 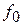 – тактовая частота;
– тактовая частота;  . При
. При 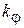 = 1
= 1
 .
.
С приходом каждого тактового импульса в сумматоре суммируются значения чисел, записанных в регистре данных и в частотном регистре, и сумма переписывается вновь в регистр данных. Таким образом, в накопителе формируется код текущей фазы мгновенного значения выходного колебания. Как только значение текущей фазы в накопителе превысит  (
( превысит
превысит  , где
, где  – номер приходящего тактового импульса), произойдет переполнение, в регистр данных запишется разность между последним значением текущей фазы и
– номер приходящего тактового импульса), произойдет переполнение, в регистр данных запишется разность между последним значением текущей фазы и  , и процесс накопления фазы повторится.
, и процесс накопления фазы повторится.
В соответствии с кодом числа в накопителе преобразователь кодов вырабатывает код амплитуды выходного сигнала ЦВС, пропорциональной 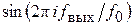 . При этом на выходе ЦАП появляется импульс постоянной длительности
. При этом на выходе ЦАП появляется импульс постоянной длительности 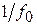 , имеющий амплитуду
, имеющий амплитуду 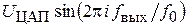 .
.
Непрерывная последовательность выходных импульсов ЦАП представляет собой ступенчатую аппроксимацию синусоидального напряжения. Изменяя дискрет фазы, код которой записан в ЧР, можно изменять частоту выходного сигнала ЦВС.
Для сокращения необходимого объема блока памяти в ПК хранится информация только для значений текущей фазы в пределах первого квадранта, она же используется и для остальных трех квадрантов с соответствующей коррекцией фазы. Более того, в блоке памяти обычно происходит квантование по фазе, т. е. в нем записаны коды значения синусоиды только для ряда дискретных значений фазы в пределах угла 0…  . Если число таких значений
. Если число таких значений 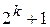 , то шаг квантования фазы
, то шаг квантования фазы
 (k < n). (2.7)
(k < n). (2.7)
Вместо блока памяти может использоваться блок вычислений, в котором по определенной программе вычисляется код амплитуды, соответствующей текущему значению кода фазы.
Текущие значения амплитуды синтезируемого синусоидального сигнала также квантованы, а относительная величина шага квантования равна  , где m – разрядность ЦАП.
, где m – разрядность ЦАП.
Квантование фазы в блоке памяти и мгновенных значений напряжения на выходе ЦАП приводит к отклонениям синтезированного колебания от моногармонического, характеризуемым уровнями фазового  и амплитудного
и амплитудного  шума.
шума.
Для определения уровня фазового шума первоначально допустим, что разрядность ЦАП настолько велика, что наличием амплитудного шума можно пренебречь. Далее учтем, что отклонения квантованных значений фазы от действительных случайны и равномерно распределены в интервале между  и
и 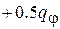 . Тогда плотность вероятности этих отклонений будет
. Тогда плотность вероятности этих отклонений будет  , а их дисперсия –
, а их дисперсия –
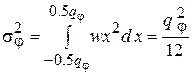 . (2.8)
. (2.8)
В соответствии с (1.7)
 , (2.9)
, (2.9)
где  – спектральная плотность мощности фазового шума.
– спектральная плотность мощности фазового шума.
Спектральная плотность мощности самого напряжения, вызванного шумом квантования фазы, при отстройке  от средней частоты
от средней частоты 
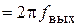 , учитывая комментарии, сделанные при выводе соотношения (2.3), будет определяться выражением
, учитывая комментарии, сделанные при выводе соотношения (2.3), будет определяться выражением 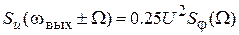 , где
, где 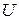 – амплитуда выходного напряжения. Считая, что
– амплитуда выходного напряжения. Считая, что  достаточно быстро убывает с ростом
достаточно быстро убывает с ростом 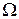 , определим среднеквадратическое значение суммы всех побочных спектральных составляющих:
, определим среднеквадратическое значение суммы всех побочных спектральных составляющих:
 =
=  . (2.10)
. (2.10)
Далее, подставив (2.7)–(2.9) в (2.10), окончательно найдем
 = 10
= 10 
 .
.
При оценке шума квантования амплитуды положим, что фазовым шумом можно пренебречь, т. е. число уровней квантования фазы достаточно велико. Далее, как и ранее, допустим, что отклонение реального значения амплитуды от квантованного является случайной величиной с равномерным законом распределения и лежит в пределах от  до
до  . Тогда плотность вероятности отклонения амплитуды составит
. Тогда плотность вероятности отклонения амплитуды составит  , а его дисперсия, т. е. квадрат среднеквадратического отклонения амплитуды,
, а его дисперсия, т. е. квадрат среднеквадратического отклонения амплитуды, 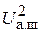 =
= 
 . С учетом последнего равенства для оценки относительного уровня шума квантования амплитуды будет справедливо следующее выражение:
. С учетом последнего равенства для оценки относительного уровня шума квантования амплитуды будет справедливо следующее выражение:
 .
.
В соответствии с теоремой Котельникова 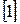 частота тактовых импульсов должна быть по крайней мере в два раза выше максимальной частоты формируемых колебаний. Для облегчения фильтрации гармоник тактовой частоты
частота тактовых импульсов должна быть по крайней мере в два раза выше максимальной частоты формируемых колебаний. Для облегчения фильтрации гармоник тактовой частоты  обычно выбирают из условия
обычно выбирают из условия  .
.
Форма выходного сигнала ЦВС близка к синусоидальной, если  >>
>> 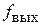 (
(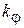 <<
<<  ), а
), а 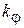 в целое число раз меньше
в целое число раз меньше  . В этом случае в конце каждого цикла накопления фазы нет остатка. Если
. В этом случае в конце каждого цикла накопления фазы нет остатка. Если 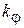 по значению сравнимо с
по значению сравнимо с  , форма выходного сигнала может существенно отличаться от требуемой гармонической. Если же
, форма выходного сигнала может существенно отличаться от требуемой гармонической. Если же 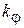 ¹
¹  (p – целое число, меньшее n), период сформированного колебания будет определяться наибольшим общим делителем
(p – целое число, меньшее n), период сформированного колебания будет определяться наибольшим общим делителем  чисел
чисел 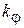 и
и  и станет равным
и станет равным  . При этом в спектре выходного сигнала ЦВС появятся дискретные составляющие, следующие с интервалом
. При этом в спектре выходного сигнала ЦВС появятся дискретные составляющие, следующие с интервалом  . Для снижения уровня спектральных составляющих на частоте
. Для снижения уровня спектральных составляющих на частоте  и ее гармониках на выходе ЦВС включается фильтр нижних частот с граничной частотой несколько выше
и ее гармониках на выходе ЦВС включается фильтр нижних частот с граничной частотой несколько выше  .
.
Рассматриваемый ЦВС с успехом может быть использован и в тех случаях, когда необходимо синтезировать сигнал, форма которого отличается от синусоидальной, например периодическую последовательность прямоугольных, треугольных, пилообразных и т. п. импульсов. Для этого достаточно в схеме рис. 2.6 применить преобразователь кодов, в котором каждому текущему значению кода фазы будет соответствовать код амплитуды сигнала требуемой формы.
Отметим, что серийно выпускаемые интегральные пассивные цифровые ССЧ имеют тактовую частоту 300…1000 МГц, разрядность НФ – от 32 до 48, разрядность ЦАП – 10…14, что обеспечивает уровень высших гармоник не более  дБ [7]. В состав интегральной микросхемы могут быть включены дополнительные узлы, обеспечивающие формирование сигналов с различными видами модуляции и манипуляции (см. 2.4). Кроме того, интегральные схемы ЦВС зачастую имеют в своем составе и основные узлы умножителя частоты на основе ССЧ с ФАП. Это связано с тем, что источником колебаний с тактовой частотой
дБ [7]. В состав интегральной микросхемы могут быть включены дополнительные узлы, обеспечивающие формирование сигналов с различными видами модуляции и манипуляции (см. 2.4). Кроме того, интегральные схемы ЦВС зачастую имеют в своем составе и основные узлы умножителя частоты на основе ССЧ с ФАП. Это связано с тем, что источником колебаний с тактовой частотой  является опорный кварцевый генератор. Рабочая частота высокостабильных ОКГ
является опорный кварцевый генератор. Рабочая частота высокостабильных ОКГ  , как правило, не превышает 10 МГц, что существенно меньше требуемых значений
, как правило, не превышает 10 МГц, что существенно меньше требуемых значений  . Поэтому между ОКГ и схемой управления и синхронизации ЦВС включается умножитель частоты, обычно выполняемый на основе рассматриваемого далее кольца ФАП с делителем в цепи обратной связи.
. Поэтому между ОКГ и схемой управления и синхронизации ЦВС включается умножитель частоты, обычно выполняемый на основе рассматриваемого далее кольца ФАП с делителем в цепи обратной связи.
|
|
|



