Вычисление коэффициента корреляции для большой выборки

При вычислении статистик связи для большой выборки данные группируются в корреляционную решетку и проводятся дополнительные расчеты:

1. Определите условные центры по ряду X и Y - это классы, имеющие наибольшую частоту или близкие к середине ряда. В нашем случае в ряду X условное средне X_o =32, в ряду Y - Y_o =26.

2. Рассчитайтеусловные отклонения:

Ai =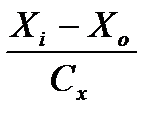

Bi =

где: X_i, Y_i – это отдельные значения вариант по ряду X и Y.

Часть отклонений имеет знак «+», другая часть – «-».

3. Далее заполните графы в соответствии с формулами, записанными в таблице:

A_in_i,B_jn_j, - умножьте условные отклонения насоответствующие им частоты, как по ряду X, таки Y;

A_i²n_i, B_j²n_j -перемножьтеквадраты условныхотклонений на соответствующие частоты, как по ряду X, таки Y;

∑B_jn_i, -– последовательно суммируйтепроизведения условныхотклонений B_j по классам на соответствующие частоты n_i; (расчеты проводятся по строкам);

Пример: расчеты по первой строке

1*(-6)+5*(-5)*1*(4)=-35.

∑B_jn_iA_i– рассчитанное значение ∑B_jn_i умножьтеусловное отклонение по ряду XA_i: -35*(-2)= 70;

4. Следующим этапом вычислите средние по классам по ряду X и Y, как средневзвешенное с учетом веса каждого класса (частоты):

Пример:

5. Расчет:

· моментов

m1x= =	m2x= =
m1y= =	m2y= =
mxy= =
· средних квадратических отклонений по ряду X и Y:
=	=

· коэффициента корреляции R:

R = = .

· ошибки коэффициента корреляции m_R:

· критерия достоверности Стьюдента t_ф

t_ф = = .

Коэффициент корреляции R=0,828, можно сделать вывод - теснота связи между диаметром на высоте груди и высотой деревьев – высокая.

 

Таблица 5.1

Построение корреляционной решетки между изучаемыми признаками __ H _ и _ D ___

Признаки	Высота, м	Час-тота, nx	Ai	Aini	Ai2ni	Sbjni	SbjAini	Средние по клссам
Действительные значения классов по H
Действительные значения класов по_ D _													-3	-21		-35		21,0
												-2	-20		-26		23,4
												-1	-15		-30		24,0
															-14		25,0
															-1	-1	25,9
																	27,0
																	27,0
																	26,5
																	29,0
ny																-88
bj		-6	-5	-4	-3	-2	-1
bjnj		-6	-25	-24	-21	-22	-13					-88	S
bj2nj													S
Средние по клссам			25,33	25,14	30,18	31,69	34,82	40,50	40,00	52,00

· коэффициент детерминации R²

R²=0,686 – означает, что диаметр на высоте груди объясняет на
68,6 % изменчивость высоты деревьев, остальные 31,4% приходится на другие факторы, не вошедшие в анализ.

· Число степеней свободы df = N-2=75-2=73

· Критерий достоверности Стьюдента табличный (Прил.1 ) tRst5% =1,96

Выводы:

Сравниваем t_ф>t_{st5% ,} 12,63>1,96, делаем вывод, чтодостоверность коэффициента корреляции высокая на 5% уровне значимости. Между диаметром деревьев и высотой наблюдается положительная связь, теснота которой - высокая.

2.Вычисление корреляционного отношения для большой выборки:

Заполните вспомогательнуюТабл.5.2. Данные для граф 1-4 берутся из Табл.5.1. Далее расчеты ведутся согласно формулам.

Таблица 5.2

Таблица расчетов

Xi	Частота, ni	Ai	Sbjni	(Sbjni)2
		3	4	5
		-3	-35
		-2	-26		67,6
		-1	-30
			-14
			-1		0,083
					0,5
Итого:			-88		340,18

Подведите итоги под графами 4, 6.

Произведите расчеты:

· моментов

m₂ =

· корреляционного отношения:

h = 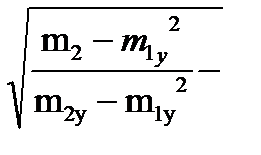= - высокая связь

· ошибкии достоверности корреляционного отношения:

mη= tф = = .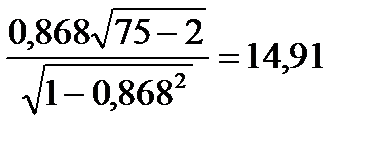

Выводы:

Сравниваем t_ф>t_{st5% ,} 14,91>1,96, делаем вывод, чтодостоверность корреляционного отношения высокая на 5% уровне значимости. Статистику можно использовать для анализа.

 

3. Расчет коэффициента линейности связи:

e=h²-r²=0,868-0,828=0,067

me =±

te =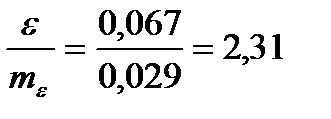

Проведите сравнение t_e и t_stα.

Если t_e > t_stα, то связь криволинейная, в ином случае прямолинейная.

В нашем примере 2,31>1,96, уровень значимости 5%. Связь слабо криволинейная.

ПРАКТИЧЕСКАЯ РАБОТА № 5 (часть 2)

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: