Среднее квадратическое отклонение

Является наиболее совершенной характеристикой вариации. Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:

Среднее квадратическое отклонение простое:

Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:

Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1,25.

Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.

Коэффициент осцилляции, линейный коэф. вариации, коэф.вариации.

(Относительные показатели вариации)

Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней:

Коэффициент осцилляции (v_R) рассчитывается по формуле:

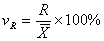
И отражает относительную меру колеблемости крайних значений признака вокруг средней.

Линейный коэффициент вариации (v_d) рассчитывается по формуле:

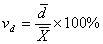
И отражает долю усреднённого значения абсолютных отклонений от средней величины.

Коэффициент вариации (v_σ ) как относительное квадратическое отклонение от средней величины рассчитывается по формуле:

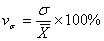
На практике чаще всего вычисляют коэффициент вариации. Нижней границей этого показателя является нуль, верхнего предела он не имеет, однако известно, что с увеличением вариации признака увеличивается и его значение. Коэффициент вариации является в известном смысле критерием однородности совокупности (в случае нормального распределения).

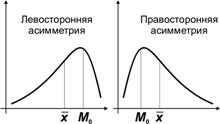
Ассиметрия: левосторонняя, правосторонняя

В симметричных распределениях средняя арифметическая, мода и медиана совпадают (. Если это равенство нарушается — распределение ассиметрично..

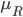В качестве обобщающих характеристик вариации используются центральные моменты распределения -го порядка , соответствующие степени, в которую возводятся отклонения отдельных значений признака от средней арифметической:

Для несгруппированных данных:

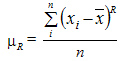
Для сгруппированных данных:

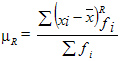
Момент первого порядка 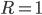согласно свойству средней арифметической равен нулю .

Момент второго порядка является дисперсией .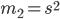

Моменты третьего 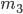и четвертого 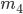порядков используются для построения показателей, оценивающих особенности формы эмпирических распределений.

С помощью момента третьего порядка измеряют степень ассиметричности распределения.

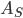— коэффициент ассиметрии

В симметричных распределениях 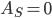, как все центральные моменты нечетного порядка. Неравенство нулю центрального момента третьего порядка указывает на асимметричность распределения. При этом, если , то асимметрия правосторонняя; если 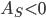, то асимметрия левосторонняя.

Коэффициент эксцесса

Для характеристики островершинности или плосковершинности распределения вычисляют отношение момента четвертого порядка (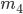) к среднеквадратическому отклонению в четвертой степени (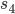). Для нормального распределения , поэтому эксцесс находят по формуле: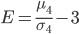

Для нормального распределения 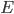обращается в нуль. Для островершинных распределений , для плосковершинных .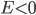

Выборочное наблюдение

Выборочным называется такое несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, а полученные в процессе исследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: