Простая случайная выборка.

Простая случайна выборка заключается в отборе единиц из генеральной совокупности в целом без разделения ее на группы, подгруппы или серии отдельных единиц.

Расчет средней ошибки повторной простой случайной выборки производится следующим образом:

где числитель — дисперсия признака х в выборочной совокупности;
n — численность выборочной совокупности.

Расчет средней ошибки бесповторной случайной выборки:

Где N — объем генеральной совокупности; n — объем выборки.

Границы генеральной средней (теорема Маркова).

Генеральной средней называют среднее арифметическое значений признака генеральной совокупности:

.

(6.2)

где x_i – варианта генеральной совокупности, n_i – частота варианты x_i,

Если все значения признака различны, то

Зная выборочную среднюю величину признака и предельную ошибку выборки (из формулы предельной ошибки выборки), можно рассчитать границы (пределы), в которых заключена генеральная средняя:

определяющие доверительный интервал.

Средняя ошибка для бесповторной выборки.

Бесповторная выборка называется потому, что каждая из единиц после регистрации ее признаков обратно не возвращается и в дальнейшем уже в отборе не существует.

При бесповторной выборке сокращается численность единиц генеральной совокупности. Поэтому при определении ошибки выборочной средней и доли признака при бесповторном отборе должна быть учтена численность генеральной совокупности и доля выборки.
Генеральную совокупность обозначим через N, тогда доля выборочной совокупности n, будет равна . Поэтому в формулу ошибки выборки при повторном отборе должен быть введен дополнительный множитель . Тогда формулы ошибок выборки бесповторного отбора примут следующий вид:
для определения ошибки выборочной средней:

Дополнительный множитель всегда будет меньше 1.

Формулы для определения необходимого объема простой случайной повторной и бесповторной выборки.

Чтобы рассчитать численность в повторной и бесповторной простой случайной выборки, можно использовать следующие формулы:

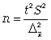(для средней при повторном способе);

(для средней при бесповторном способе);

где - предельная ошибка выборки

T-нормированное отклонение

N-объем генеральной совокупности

S-дисперсия выборки

Систематическая (механическая) выборка.

Механическая выборка применяется в тех случаях, когда генеральная совокупность каким-либо образом упорядочена.

Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотношением объеа выборки и генеральной совокупности.

Для проведения отбора желательно, чтобы все единицы генеральной совокупности имели порядковые номера от 1 до N.

Отбор единиц осуществляется в соответствии с установленными пропорциями через равные интервалы.

Необходимый объем в случае систематической выборки.

(бесповторный способ);

где - предельная ошибка выборки

T-нормированное отклонение

N-объем генеральной совокупности

S-дисперсия выборки

Типическая (стратифицированная) выборка.

Используется, когда все единицы генеральной совокупности объединены в несколько крупных типических групп, такие группы называются стратами(слоями).

Отбор единиц в типическую выборку может быть организован 2 способами:

1. Пропорционально объему типических групп(слоев).

Число единиц определяется используя принцип представительности. n_i=n*(N_i/N), где N_i – объем i-ой группы, n_i-объем выборки из i-ой группы.

Средняя ошибка вычисляется по формулам:

(повторный)

(бесповторный)

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: