 |
Формулы для объема типической выборки в вопросе 47.
|
|
|
|
- Пропорционально внутригрупповой вариации признака.
Отбор единиц в выборку заключается в пропорциональности вариации признака в типических группах. ni=n*Si*Ni/å S*Ni где Si-среднее квадратичное отклонение признака в группе с номером i.
Средняя ошибка определяется по формулам:
(1/N)* /(å S*Ni/ ni) (повторная)
(1/N)* /(å S*Ni/ ni)*(1-(ni /Ni) (бесповторная)
На практике применение способа (2) затруднено из-за сложностей в получении сведений о вариации до проведения выборочного наблюдения.
Число единиц для типической выборки пропорциональной объему типических групп.
При выборке, пропорциональной объёму типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
ni = n * 
,
Где ni – объём выборки из i-й группы; Ni – объём i-й группы; N – объем генеральной совокупности; n – численность выборочной совокупности.
Средняя из внутригрупповых дисперсий.
Внутригрупповая дисперсия (частная, остаточная, случайная) отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы (хi) от средней арифметической этой группы (xср) (групповой средней) и может быть исчислена как:
Простая дисперсия 2. взвешенная дисперсия
Средняя из внутригрупповых дисперсий по совокупности в целом - вариация значений признака под влиянием прочих факторов. На основании внутригрупповой дисперсии по каждой группе можно определить общую среднюю из внутригрупповых дисперсий:
, где
ni – число единиц выборочной совокупности
- средняя из выборочных дисперсий типических групп
|
|
|
Необходимый объем типической выборки, организованной пропорционально объему типических групп для случая: а) повторного отбора; б) бесповторного отбора.
(повторный отбор)
(бесповторный отбор), где
N - объем (число единиц) генеральной совокупности;
n - объем (число единиц) выборочной совокупности;
σ - выборочная средняя, т.е. среднее значение изучаемого признака по выборочной совокупности;
t — коэффициент доверия, определяемый по таблицам в зависимости от уровня вероятности;
∆ - предельная ошибка выборки.
Число единиц для типической выборки, организованной пропорционально вариации признака.
Отбор, пропорциональный внутригрупповой дифференциации признака, осуществляется на основе использования внутригрупповых дисперсий по каждой типической группе.
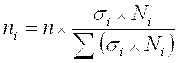(может быть неправильная формула, не нашла)
Средняя ошибка для типической выборки, организованной пропорционально вариации признака для случая: а) повторного отбора; б) бесповторного отбора.
1. Для средней количественного признака:
где Si2 — средняя из внутригрупповых дисперсий по выборочной совокупности.
2. Для доли (альтернативного признака):
где wi(1 – wi) – числитель - средняя из внутригрупповых дисперсий доли (альтернативного признака) по выборочной совокупности.
Серийная выборка.
Сущность серийной выборки заключается в собственно-случайном либо механическом отборе групп единиц (серий), внутри которых производится сплошное обследование. Единицей отбора при этой выборке является группа или серия, а не отдельная единица генеральной совокупности, как это имело место в рассматриваемых ранее выборках.
Данный способ отбора удобен в тех случаях, когда единицы генеральной совокупности изначально объединены в небольшие более или менее равновеликие группы или серии. В качестве таких серий могут выступать упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие подобные объединения.
|
|
|
В большинстве случаев серийная выборка имеет не столько методологические, сколько организационные преимуществами перед другими способами формирования выборочном совокупности. Например, в Великобритании серийный отбор используется в обследованиях населения, когда серией являются домохозяйства, объединенные общим почтовым индексом. В случайном порядке производится выборка индексов и под обследование попадают все домохозяйства, имеющие индекс попавших в выборочную совокупность матовых отделений.
|
|
|
