 |
Генеральная совокупность. Повторный отбор. Бесповторный отбор.
|
|
|
|
В выборочном наблюдении используются понятия «генеральная совокупность» — изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам, и «выборочная совокупность» — случайно выбранная из генеральной совокупности некоторая ее часть. К данной выборке предъявляется требование репрезентативности, т.е. при изучении лишь части генеральной совокупности полученные выводы можно применять ко всей совокупности.
Бесповторным называется такой отбор, при котором попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор. При этом объем генеральной совокупности по мере формирования выборки уменьшается.
При повторном отборе попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность для участия в дальнейшей процедуре отбора. В этом случае объем генеральной совокупности остается постоянным, что упрощает формулы ошибок.
На практике обычно пользуются бесповторным случайным отбором.
Ошибки репрезентативности: систематические, случайные.
Ошибки репрезентативности возникают вследствие несоответствия структуры выборки структуре генеральной совокупности. Источником их существования является разная вариация признака у статистических единиц, в результате которой распределение единиц в выборочной совокупности отличается от распределения единиц в генеральной совокупности. Ошибки репрезентативности делятся на систематические и случайные.
Систематические ошибки репрезентативности возникают из-за неправильного формирования выборки, при котором нарушается основной принцип научно организационной выборки – принцип случайности.
|
|
|
Случайные ошибки репрезентативности означают, что даже при соблюдении принципа случайности отбора единиц, расхождения между характеристиками выборки и генеральной совокупности все же имеют место.
Средняя ошибка выборки
Средняя ошибка выборки представляет из себя среднее квадратичное отклонение выборочных средних относительно генеральных средних
 |


Где n- число всех возможных выборок из генеральной совокупности
X-выборочная средняя i-ой совокупности
Подкоренное выражение в формуле представляет собой дисперсию средних.
Поскольку, как правило, генеральная средняя и неизвестна, этой формулой нельзя воспользоваться. Используют следующее соотношение:
квадрат средней ошибки (дисперсия выборочных средних) прямо пропорционален дисперсии признака х в генеральной совокупности о и обратно пропорционален объему выборки п:
 отсюда
отсюда 
Средняя ошибка выборки тем больше, чем больше вариация в генеральной совокупности, и тем меньше, чем больше объем выборки.
Вышеприведенные формулы применяются, когда отбор единиц в выборочную совокупность производится в порядке повторной выборки.
Предельная ошибка выборки
Предельная ошибка- максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления. Зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы.
Формула предельной ошибки выборки:
D= 
 =t*
=t*  ,
,
где D (дельта) - величина пред. ошибки выборки с заданной вероятностью;
t – коэффициент доверия, которому соответствуют вероятности предельной ошибки выборки;
 - средняя ошибка выборки.
- средняя ошибка выборки.
Формулы предельных ошибок выборки:
при повторном отборе:
D = t*  = t*
= t*  ,
,
|
|
|
при бесповторном отборе:
D = t*  = t
= t 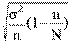
|
|
|


