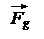|
IV. Электростатика. V. Постоянный электрический ток. Физические основы механики, молекулярной физики и термодинамики. Основные формулы
|
|
|
|
IV. Электростатика
Закон сохранения электрического заряда. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Поток вектора напряженности. Теорема Остроградского - Гаусса и ее применение к расчету электрических полей. Работа в электростатическом поле. Разность потенциалов, потенциал. Связь между потенциалом и напряженностью. Вычисление потенциала. Поле диполя. Электрическое поле в веществе. Поляризация диэлектриков. Вектор поляризации и его связь с поверхностной плотностью поляризационных зарядов. Напряженность поля внутри диэлектрика. Теорема Остроградского - Гаусса для диэлектриков. Вектор электрического смещения. Условия на границе раздела двух диэлектриков. Вычисление напряженности поля в диэлектрике. Проводнике в электрическом поле. Поле внутри проводника и у его поверхности. Электроемкость уединенного проводника. Конденсаторы. Примеры вычисления емкости. Энергия заряженного проводника и конденсатора. Энергия электростатического поля. Объемная плотность энергии.
V. Постоянный электрический ток
Постоянный электрический ток, его характеристики и условия существования. Законы Ома и Джоуля - Ленца в дифференциальной форме. Обобщенный закон Ома в интегральной форме. Разность потенциалов, электродвижущая сила, напряжение. Классическая электронная теория металлов. Вывод законов Ома и Джоуля - Ленца из электронных представлений. Сверхпроводимость. Работа выхода электронов из металла. Термоэлектронная эмиссия.
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ, МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
ОСНОВНЫЕ ФОРМУЛЫ
| Скорость мгновенная Где r- радиус-вектор материальной точки; t- время; s- расстояние вдоль траектории движения; t - единичный вектор, касательный к траектории. | v 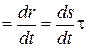
|
| Ускорение: мгновенное тангенциальное нормальное полное где R- радиус кривизны траектории; n – единичный вектор главной нормали. | а=  аt=
аt= 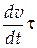 аn=
аn= 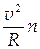 а = аt+ аn; а =
а = аt+ аn; а = 
|
| Скорость угловая где j - угловое перемещение. | 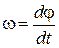
|
| Ускорение угловое Связь между линейными и угловыми величинами | 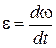 S=jR; v=wR;
аt=eR; аn =w2R
S=jR; v=wR;
аt=eR; аn =w2R
|
| Импульс материальной точки где m- масса материальной точки | p= mv |
| Основное уравнение динамики материальной точки (второй закон Ньютона) | F= 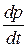 =ma =ma
|
| Закон сохранения импульса для изолированной системы | 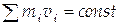
|
| Радиус-вектор центра масс | rс= 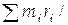 
|
| Скорости частиц после столкновения: упругого центрального неупругого где v1 и v 2 – скорости частиц до столкновения; m1 и m 2– массы частиц. | u1= -v1 +2  u2= -v2 +2
u2= -v2 +2  u1= u2 =
u1= u2 = 
|
| Сила сухого трения где f – коэффициент трения; Fn – сила нормального давления. | Fтр= f Fn |
| Сила упругости где k– коэффициент упругости (жест- кость); Dl- деформация | Fуп = k Dl |
| Сила гравитационного взаимодействия где m1 и m 2– массы частиц; G- гравитационная постоянная; r – расстояние между частицами | Fтр = G 
|
| Работа силы | А= 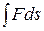
|
| Мощность | N = 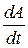 = F v = F v
|
| Потенциальная энергия: упругодеформированного тела гравитационного взаимодействия двух частиц тела в однородном гравитационном поле где g- напряженность гравитационного поля (ускорение свободного падения); h- расстояние от нулевого уровня. | П = 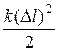 ;
П = ;
П = 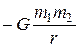 ;
П = m g h, ;
П = m g h,
|
| Напряженность гравитационного поля Земли где Мз- масса Земли; R- радиус Земли; h- расстояние от поверхности Земли. | G= 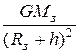 , ,
|
| Потенциал гравитационного поля Земли | j = - 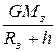 , ,
|
| Кинетическая энергия материальной точки | Т = 
|
| Закон сохранения механической энергии | E = T +П = const |
| Момент инерции материальной точки где r- расстояние до оси вращения. | J = m r2, |
| Моменты инерции тел массой m относительно оси, проходящей через центр масс: тонкостенного цилиндра (кольца) радиуса R, если ось вращения совпадает с осью цилиндра сплошного цилиндра (диска) радиуса R, если ось вращения совпадает с осью цилиндра шара радиуса R тонкого стержня длиной l, если ось вращения перпендикулярна стержню |
J0 = m R 2,
J0= 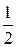 mR 2;
J0 = mR 2;
J0 = 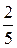 m R 2;
J0= m R 2;
J0= 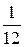 m l2. m l2.
|
| Момент инерции тела массой m относительно произвольной оси (теорема Штейнера) где J0- момент инерции относительно параллельной оси, d – расстояние между осями. | J = J0 +m d 2, |
| Момент силы где r- радиус-вектор точки приложения силы | М = r ´ F, |
| Момент импульса | L= Jw. |
| Основное уравнение динамики вращательного движения | М = 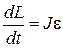 . .
|
| Закон сохранения момента импульса для изолированной системы | 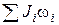 = const. = const.
|
| Работа при вращательном движении | А = 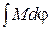
|
| Кинетическая энергия вращающегося тела | T = 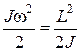
|
| Релятивистское сокращение длины где l0- длина покоящегося тела; с - скорость света в вакууме. | l = l0 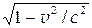 , ,
|
| Релятивистское замедление времени где t0- собственное время. | t= 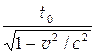 , ,
|
| Релятивистская масса где m0- масса покоя. | m= 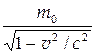
|
| Энергия покоя частицы | E0 = m0c2. |
| Полная энергия релятивистской частицы | E = m0c2= 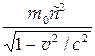
|
| Релятивистский импульс | р = mv= 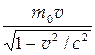
|
| Кинетическая энергия релятивистской частицы | T= E-E0= m0c2 ( 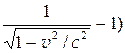 . .
|
| Релятивистское соотношение между полной энергией и импульсом | Е2 = р2с2+E02 |
| Теорема сложения скоростей в релятивистской механике где u и u¢ - скорости в двух инерциальных системах координат, движущихся относительно друг друга со скоростью v, совпадающей по направлению с u (знак “-“) или противоположно ей направленной (знак “+”). | 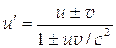 , ,
|
| Количество вещества где – N-число молекул; NА- постоянная Авогадро; m- масса вещества; M- молярная масса. | n = 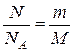 , ,
|
| Уравнение Клапейрона-Менделеева где р- давление газа; V – его объем; R-молярная газовая постоянная; T – термодинамическая температура. | pV =n RT, |
| Уравнение молекулярно-кинетической теории газов где n-концентрация молекул; < eпост> - средняя кинетическая энергия поступательного движения молекулы; m0 – масса молекулы; < vкв> - средняя квадратичная скорость. | p= 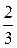 n< eпост> = n< eпост> = 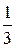 n m0< vкв> 2, n m0< vкв> 2,
|
| Средняя энергия молекулы где i- число степеней свободы; k- постоянная Больцмана. | < e> = 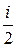 kT, kT,
|
| Внутренняя энергия идеального газа | U = 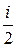 nRT nRT
|
Скорости молекул:
средняя квадратичная
средняя арифметическая
наиболее вероятная 
| < vкв> = 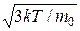 = = 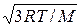 ;
< v> = ;
< v> = 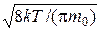 = = 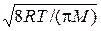 ;
< vв> = ;
< vв> = 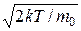 = = 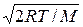 . .
|
| Средняя длина свободного пробега молекулы где d- эффективный диаметр молекулы | < l> =( 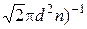
|
| Среднее число столкновений молекулы в единицу времени | < z> = 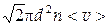
|
| Распределение молекул в потенциальном поле сил где П – потенциальная энергия молекулы. | n = n0exp  , ,
|
| Барометрическая формула | p = p0exp 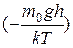 . .
|
| Уравнение диффузии где D – коэффициент диффузии; r- плотность; dS- элементарная площадка, перпендикулярная оси Ох. |
dm= -D  dS dt, dS dt,
|
| Уравнение теплопроводности где æ - теплопроводность. | dQ = -æ 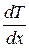 dS dt, dS dt,
|
| Сила внутреннего трения где h - динамическая вязкость | dF= -h 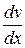 dS, dS,
|
| Коэффициент диффузии | D = 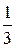 < v > < l>. < v > < l>.
|
| Вязкость (динамическая ) | h = 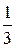 r < v > < l> = Dr r < v > < l> = Dr
|
| Теплопроводность где сn - удельная изохорная теплоемкость | æ = 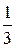 cn r< v > < l> = h cn, cn r< v > < l> = h cn,
|
| Молярная теплоемкость идеального газа изохорная изобарная |
Cn= 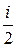 R;
Cр= R;
Cр= 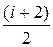 R. R.
|
| Первое начало термодинамики | dQ = dU + dA, dU = Cn dT, dA = p dV. |
| Работа расширения газа при процессе изобарном изотермическом адиабатном где g=Ср /Сn |
A = p (V2-V1)= nR(T2-T1);
A=n RT ln 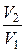 =n RT ln =n RT ln 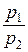 ;
A = n Cn(T1-T2)= ;
A = n Cn(T1-T2)=
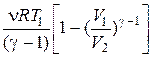 =
= =
= 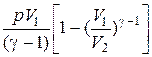 , ,
|
| Уравнения Пуассона | pV g = сonst TV g-1 = сonst Tgp g-1 = сonst |
| Коэффициент полезного действия цикла Карно где Q и Т – количество теплоты, полученное от нагревателя, и его температура; Q0 и Т0 – количество теплоты, переданное холодильнику, и его температура | h = 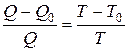
|
| Изменение энтропии при переходе из состояния 1 в состояние 2 | S2 –S1= 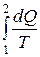
|
|
|
|
|
|
|
|
|
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. Тело массой m = 1, 00 кг, двигаясь по горизонтальной поверхности, сталкивается с горизонтальной пружиной, жесткость которой k = 0, 20 кН/м, а масса пренебрежимо мала. Тело сжимает пружину на s = 1, 0 см, считая от ее недеформированного положения. Коэффициент трения между телом и поверхностью m = 0, 50. Какова скорость тела в момент соударения?
|
|
|
|
Решение | |||||
 m = 1, 00 кг m = 1, 00 кг
| Изменение кинетической энергии тела равно работе | ||||
| k = 0, 20 кН/м | сил, действующих на него: | ||||
| s = 1, 0 см | DWк = Wк2 – Wк1 = А. | (1) | |||
| m = 0, 50 | В рассматриваемом случае | ||||
| Wк1 = mv 2 / 2, Wк2 = 0. | |||||
| v -? | Внешними силами являются сила трения скольжения | ||||
|
| 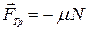 
|
| (2) | ||
где N - сила реакции опоры, и сила упругости пружины
 , ,
| (3) |
где r - величина деформации.
Так как N = mg, то модуль силы трения равен Fтр= m mg .
Работа силы трения на пути s равна
| Атр= – m mgs . | (4) |
Работа силы упругости при сжатии пружины на величину s
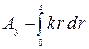 = – k s2/2. = – k s2/2.
| (5) |
Из (1), (4), (5) следует:
| mv 2 / 2 = m mgs + k s2/2. | (3) |
Таким образом
v = 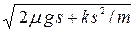 . .
| (4) |
Проверка (4) на размерность:
[v ] = (( м/с2)м + (Н/м)м2/кг)0, 5 = ( м2/с2 + (кг× м/м× с2)м2/кг)0, 5 = м/с.
Вычисления:
v = (2 × 0, 50× 9, 8× 10-2 + 0, 20× 103× 10- 4/ 1, 0) 0, 5 = 3, 4 (м/с).
Ответ: скорость тела в момент соударения v = 3, 4 м/с.
2. Сплошной однородный диск скатывается без скольжения с наклонной плоскости, образующей угол a = 30° с горизонтом. Определить линейное ускорение центра диска.
|
Решение | ||
| a = 30° | На тело действуют сила тяжести | ||
| реакция опоры | |||
| а -? | Уравнения движения тела имеют вид: | ||
| где
Момент импульса тела относительно оси Z, |
| ||
проходящей через центр масс диска перпендикулярно плоскости XY равен
| Lz = I z w, | (3) |
где
| I z = m R2 / 2 - | (4) |
– момент инерции диска массы m и радиуса R относительно оси Z. Момент
силы трения относительно оси Z равен
| MТр = FТр R, | (5) |
моменты силы тяжести и реакции опоры относительно оси Z равны нулю.
Таким образом, уравнение (1) в проекции на ось Х имеет вид
| ma = mg sina - FТр, | (6) |
уравнение (2) в проекции на ось Z
| I z e = FТр R, | (7) |
где 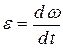 - угловое ускорение.
- угловое ускорение.
В отсутствие проскальзывания e = а/ R. Тогда из (4), (5), (7) следует:
| ma = 2 FТр |
и с учетом (6) –
| a = ( 2/3) g sina | (8) |
Проверка формулы (8) на размерность очевидна.
Вычисления:
a = ( 2/3) × 9, 81× sin30° = 3, 27 (м/с2)
Ответ: ускорение центра масс диска равно a = 3, 27 м/с2.
|
|
|
3. В сосуде объемом 30 л находится смесь водорода и гелия при температуре 300 К и давлении 832 кПа. Масса смеси равна 24 г. Определить массу водорода, массу гелия, плотность и молярную массу смеси.
|
Решение | ||||
| V = 3, 0× 10-2 м3 | Для каждой компоненты данной смеси применимо уравнение Менделеева-Клапейрона: | |||
| Т = 300 К | p1 V = m1 RT/ m1 ; | (1) | ||
| p = 8, 32 × 105 Па | p2 V = m2 RT/ m2 , | (2) | ||
 m =2, 4× 10-2 кг m =2, 4× 10-2 кг
| где p1 – парциальное давление водорода, m1 – масса | |||
| m1 = 2 × 10-3 кг/моль | водорода, m1 – его молярная масса, V – объем сосуда, | |||
| m2 = 4 × 10-3 кг/моль | Т – температура газа, R = 8, 31 Дж/(моль× К) – универ- | |||
| сальная газовая постоянная, p2 – парциальное | ||||
| m1, m2, r, m -? | давление гелия, m2 – масса гелия, m2 – его молярная | |||
| масса. | ||||
Согласно закону Дальтона давление смеси газов равно сумме парциальных давлений компонент данной смеси:
| p = p1 + p2 . | (3) |
Из (1)-(3) следует:
| p V = ( m1 / m1 + m2 / m2 ) RT | (4) |
Так как m = m1 + m2 , то из (4) следуют выражения для массы водорода и массы гелия:
| m1 = m1 ( m2 pV/ RT - m ) /(m2 - m1) | (5) | ||
| m2 = m2 ( m - m1 pV/ RT ) /(m2 - m1) | (6) |
Проверка формул (5), (6) на размерность:
[m] = ( кг/моль)(( кг/моль)Па× м3/(Дж/(моль× К) × К - m)/(кг/моль) = кг× Н× м× /Дж = кг.
Плотность вещества определяется формулой:
| r = m / V . | (7) |
Молярная масса смеси находится по формуле
| m = m / (n1 + n2), | (8) |
где n1 = m1 / m1, n2 = m2 / m2 - число молей водорода и гелия соответственно.
Из ( 4) и (8) следует:
| m = m RT / p V. | (9) |
Проверка формулы (9) на размерность:
[m] = кг (Дж/(моль× К)) × К / Па× м3 = (кг /моль) Дж / Н× м = кг /моль
Вычисления:
m1 = 2× 10-3(4× 10-3× 8, 32× 105× 3, 0× 10-2/8, 31× 300-2, 4× 10-2)/(4- 2)× 10-3 = 1, 6× 10-2 (кг);
m2 = 4× 10-3(2, 4× 10-2 - 2× 10-3× 8, 3× 105 × 2, 0× 10-2/8, 31× 300)/(4- 2)× 10-3 = 0, 8× 10-2 (кг);
r = 2, 4× 10-2 / 3, 0× 10-2 = 0, 80 (кг/м3);
m = 0, 240 × 8, 31× 300/ 830× 103× 0, 200 = 3, 60× 10-3 (кг /моль).
Ответ: масса водорода m1 = 16 г; масса гелия m2 = 8 г;
плотность смеси r = 0, 80 кг/м3; молярная масса смеси m = 3, 60× 10-3 кг /моль.
4. Объем углекислого газа, находящегося под давлением 110 кПа, увеличился от 1, 00 л до 2, 00 л. Определить количество теплоты, изменение внутренней энергии и работу расширения газа, если расширение происходило 1) изотермически; 2) изобарно; 3) адиабатно.
|
Решение | |||||||
| p = 1, 10× 105 Па | Согласно первому началу термодинамики, количество | ||||||
| V1 =1, 00 × 10-3 м3 | теплоты Q, полученное газом, расходуется на | ||||||
V2 =2, 00 × 10-3 м3
 m = 44 × 10-3 кг/моль m = 44 × 10-3 кг/моль
| увеличение его внутренней энергии U и на совершенную им работу А: | ||||||
| i = 6 |
| Q = DU + А. | (1) | ||||
| 1) Т = const | Внутренняя энергия идеального газа определяется | ||||||
| 2) p = const | выражением: | ||||||
| 3) Q = 0 |
| U = ( i /2) m RT/ m | (2) | ||||
| DU ; А; Q -? | или с учетом уравнения Менделеева-Клапейрона: | ||||||
|
| p V = m RT/ m | (3) | |||||
|
| U = ( i /2) p V, |
| (4) | ||||
где p, Т , V, m – давление температура, объем и масса газа, m. i - молярная масса газа и число степеней свободы его молекул.
Работа газа при изменении его объема определяется по формуле:
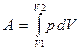 . .
| (5) |
1) В изотермическом процессе (Т = const) согласно (2) U = const, DU=0 .
Так как p = m RT/ V m, то
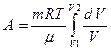 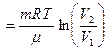 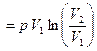 . .
| (6) |
Проверка формулы (6) на размерность:
[А] = Па × м 3 = Н× м = Дж.
Вычисления:
[А] = 1, 10× 105 × 1, 00 × 10-3 × ln 2 = 76 (Дж).
Согласно (1) в данном случае Q = А.
2) В изобарном процессе ( p = const ) согласно (4)
| D U = ( i /2) p ( V2 - V1 ), | (7) |
Проверка формулы (7) на размерность:
[D U ] = Па × м 3 = Н× м = Дж.
Вычисления:
D U = ( 6/2) × 1, 10× 105 × ( 2, 00 × 10-3 - 1, 00 × 10-3) = 330 (Дж).
Согласно (5) в данном случае
| А = p ( V2 - V1 ) | (8) |
Проверка формулы (8) на размерность:
[ А ] = Па × м 3 = Н× м = Дж.
Вычисления:
А = 1, 10× 105 × ( 2, 00 × 10-3 - 1, 00 × 10-3) = 110 (Дж).
Количество теплоты, полученное газом в данном процессе в соответствии с (1), (7), (8) находится по формуле
| Q = (( i /2) + 1 ) p ( V2 - V1 ) | (9) |
Проверка формулы (9) на размерность аналогична проверке формул (7) и (8).
Вычисления:
Q = (3 +1) × 1, 10× 105 × ( 2, 00 × 10-3 - 1, 00 × 10-3) = 440 (Дж).
В адиабатном процессе ( Q = 0 ) согласно (1)
| DU = - А. | (10) |
Вычисление величины DU в данном случае проводится с помощью формулы (4):
| D U = ( i /2) ( p2 V2 - p1 V1 ) | (11) |
В соответствии с уравнением Пуассона
| p V g = const, | (12) |
где g = ( i + 2 )/ i
| p2 = p1 (V1 /V 2)g. | (13) |
Согласно (10), (11), (12)
| D U = ( i /2) p1V1 ((V1 /V 2)g-1 - 1 ) | (14) | ||
| А = ( i /2) p1 V1 ( 1 -(V1 /V 2)g-1 ) | (15) |
Проверка формул (14), (15) на размерность аналогична проверке формул (7) и (8).
Вычисления:
g = ( 6+ 2 )/6 = 1, 33; D U = 3 × 1, 10× 105 × 1, 00 × 10-3 ( 0, 5 0, 4 - 1) = - 73, 2 (Дж);
А = 61 Дж.
Ответ: 1) в изотермическом процессе D U = 0; А = 76 Дж. Q = 76 Дж;
2) в изобарном процессе D U = 330 Дж; А = 110 Дж; Q = 440 Дж;
3) в адиабатном процессеD U = - 73, 2 Дж; А =73, 2 Дж; Q = 0.
|
|
|



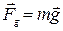 , сила трения
, сила трения 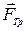 и
и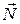 .
.  , (1)
, (1)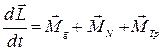 , (2)
, (2)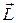 - момент импульса тела,
- момент импульса тела, 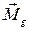 ,
, 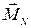 ,
, 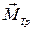 - соответственно моменты силы трения, реакции опоры и силы трения.
- соответственно моменты силы трения, реакции опоры и силы трения.