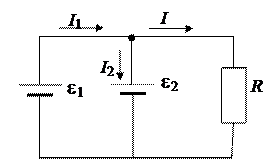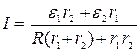|
Основы электродинамики. Основные формулы. Решение. 1. В вершинах квадрата со стороной а = 0,10 м находятся одинаковые положительные заряды q1 = 2,0 нкл, q2 = - q1, q3 = q4 = q1. Определить напряженность и потенциал электрического поля в центре
|
|
|
|
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
ОСНОВНЫЕ ФОРМУЛЫ
| Закон Кулона где q1 и q2 - величины точечных зарядов; ε 0 – электрическая постоянная; ε – диэлектрическая проницаемость среды; r – расстояние между зарядами. | F 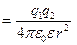 , ,
|
| Напряженность электрического поля | Е =  , ,
|
| Напряженность поля: точечного заряда бесконечно длинной заряженной нити равномерно заряженной бесконечной плоскости между двумя разноименно заряженными бесконечными плоскостями где τ – линейная плотность заряда; σ – поверхностная плотность заряда; r – расстояние до источника поля. | 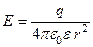 , ,
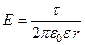 , ,
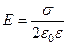 ; ;
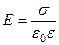 , ,
|
| Электрическое смещение | D = ε 0ε Е. |
| Работа перемещения заряда в электростатическом поле где φ 1 и φ 2 - потенциалы начальной и конечной точек. | A = 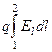 = q(φ 1 – φ 2), = q(φ 1 – φ 2),
|
| Потенциал поля точечного заряда | φ = 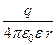 . .
|
| Связь между потенциалом и напряженностью | 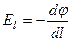 . .
|
| Сила притяжения между двумя разноименно заряженными обкладками конденсатора где S – площадь пластин. | 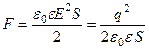 , ,
|
| Электроемкость: уединенного проводника плоского конденсатора слоистого конденсатора где d – расстояние между пластинами конденсатора; di – толщина i-го слоя диэлектрика; ε i - его диэлектрическая проницаемость. | 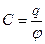 ; ;
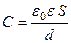 ; ;
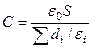 , ,
|
| Электроемкость батареи конденсаторов, соединенных: параллельно последовательно |
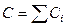 ; ;
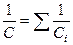 . .
|
| Энергия поля: заряженного проводника заряженного конденсатора где V – объем конденсатора. |  ; ;
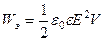 , ,
|
| Объемная плотность энергии электрического поля | 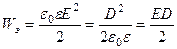
|
| Сила тока |  . .
|
| Закон Ома: в дифференциальной форме в интегральной форме где γ – удельная проводимость; ρ – удельное сопротивление; U – напряжение на концах цепи; R – сопротивление цепи; j – плотность тока. |
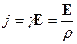 ; ;
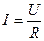 , ,
|
| Закон Джоуля – Ленца: в дифференциальной форме в интегральной форме |
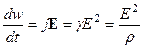 ; ;
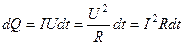 . .
|
| Сопротивление однородного проводника где l – длина проводника; S – площадь его поперечного сечения. | 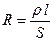 , ,
|
| Зависимость удельного сопротивления от температуры где α – температурный коэффициент сопротивления; t – температура по шкале Цельсия. | ρ = ρ 0(1 + α t), |
|
|
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. В вершинах квадрата со стороной а = 0, 10 м находятся одинаковые положительные заряды q1 = 2, 0 нКл, q2 = - q1, q3 = q4 = q1. Определить напряженность и потенциал электрического поля в центре квадрата.

|
Решение | |
| а = 0, 10 м | Согласно принципу суперпозиции, напряженность поля | |
| q 1 = 2, 0 нКл | в центре квадрата (т. О) | |
| q2 = - q1 | равна | |
| q3 = q4 = q1 | 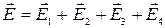
| |
Так как 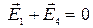 , ,
| ||
| E, j -? | то 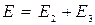 , где , где
| |
|
| ||
Проверка на размерность:
[E ] = Кл/ ((Ф/м)× м 2) = В × Ф/ ((Ф/м)× м 2) = В/м.
Вычисления:
E =2, 0× 10-9/ (3, 14 × 8, 85× 10-12 × 0, 102) = 7, 2 (В/м)
Потенциал поля в т. О находится по формуле
| j = j1 + j2 + j 3 + j4, |
где j i 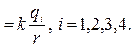 Следовательно j
Следовательно j 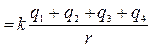
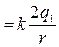 ,
,
j 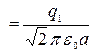 .
.
Проверка на размерность:
[j ] = Кл/ ((Ф/м)× м ) = В × Ф/ ((Ф/м)× м ) = В.
Вычисления:
j =2, 0× 10-9/ ( 1, 41× 3, 14 × 8, 85× 10-12 × 0, 10) = 0, 51 (кВ)
Ответ: В центре квадрата напряженность электрического поля 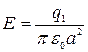 = 7, 2 В/м,
= 7, 2 В/м,
потенциал поля j 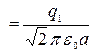 = 0, 51 кВ.
= 0, 51 кВ.
2. Между пластинами плоского конденсатора, заряженного до разности потенциалов U = 60 В, находятся два слоя диэлектриков: фарфора (e1 = 7, 0) толщиной d1 = 3, 5 мм и эбонита (e2 = 3, 0) толщиной d2 = 1, 5 мм. Площадь пластин конденсатора S = 200 см2 . Найти: электроемкость конденсатора С, напряженность
|
|
|
электрического поля E1, E2 и разность потенциалов U1, U2 в каждом слое.

|
Решение | ||||
| U = 60 В | Разность потенциалов пластин конденсатора равна | ||||
| e1 = 7, 0 | U = U1 + U2 = E1 d1+ E2 d2, (1) | ||||
| d1= 3, 5 мм | где e0 e1 E1 = e0 e2 E2 = D , | (2) | |||
| e2 = 3, 0 | Из (1) и (2) следует: U = e1 E1( d1/ e1 + d2/ e2 ). Тогда |
| |||
| d2 = 1, 5 мм | Проверка размерности в (3). (4) очевидна: [E] = В /м. Вычисления: E1 = 60 / (3, 5× 10-3 + 1, 5× 10-3 × 7, 0/ 3, 0) = 8, 6 (кВ/м), E2 = 60 / (3, 5× 10-3 × 3, 0/ 7, 0 + 1, 5× 10-3) = 20 (кВ/м). | (3), (4) | |||
| S = 200 см2 |
| ||||
|
| |||||
| С, E1, E2, |
| ||||
| U1, U2 -? |
| ||||
| Согласно (1), (3), (4) | | (5), (6) | |||
Вычисления:
U1 = 60 × 3, 5 × 10-3 / (3, 5× 10-3 + 1, 5× 10-3 × 7, 0/ 3, 0) = 30 (В),
U2 = 60× 1, 5× 10-3 / (3, 5× 10-3 × 3, 0/ 7, 0 + 1, 5× 10-3) = 30 (В).
Емкость конденсатора определяется выражением
| С = Q / U, | (7) |
где Q - заряд на пластинах конденсатора.
Так как Q = s S, где s - поверхностная плотность заряда, а s = D, то
| С = e0 e1 E1 S / U | и с учетом (3) |
| |||
| | (8) | ||||
Проверка размерности в (8):
[С] = (Ф /м) × м2 / м = Ф.
С = 8, 85× 10-12 × 200 × 10-4 / (3, 5× 10-3 / 7, 0 + 1, 5× 10-3 / 3, 0) = 0, 18 (нФ).
3. Два источника тока с ЭДС e1 = 2, 0 В и e2 = 1, 5 В и внутренними сопротивлениями r1 = 0, 4 Ом и r2 = 0, 3 Ом включены параллельно сопротивлению R = 5, 0 Ом. Определить силу тока через сопротивление.
|
Решение | |||||
 e1 = 2, 0 В e1 = 2, 0 В
| Согласно правилам | | |||
| e2 = 1, 5 В | Кирхгофа | ||||
| r1 = 0, 40 Ом | I1 - I2 = I, | ||||
| r2 = 0, 25 Ом | I1 r1 + IR =e1, | ||||
| R = 5, 0 Ом | -I2 r2 + I R = e2. | ||||
| Отсюда следует: | |||||
| I -? | |||||
|
|
| ||||
Проверка на размерность:
[I ] = В × Ом/ Ом2 = В / Ом = А.
Вычисления:
|
|
|
I = ( 2, 0 × 0, 25 + 1, 5 × 0, 40 ) / ( 5, 0 × ( 0, 40 + 0, 25) + 0, 40× 0, 25) = 0, 34 (А).
Ответ: Сила тока через сопротивление R I = 0, 34 А.
4. Батарея состоит из п = 3 последовательно соединенных источников с
с ЭДС e1 = 2, 0 В и внутренним сопротивлением r1= 0, 3 Ом каждого. Чему равна наибольшая мощность, которую можно получить от батареи?

|
Решение | ||
| e1 = 2, 0 В |
| ||
| r1= 0, 3 Ом | На внешнем участке цепи с сопротивлением R выделяется | ||
| п = 3 | мощность | ||
| Рm-? | P = I 2 R. | (1) | |
| Ток, протекающий в цепи, определяется по Закону Ома | |||
| I = e / ( R + r ), | (2) | ||
где e = пe1 , r = п r1 - соответственно ЭДС и внутреннее сопротивление батареи из п последовательно соединенных источников.
Согласно (1) и (2)
| P = e2 R / ( R + r )2 (3) |
Максимальная мощность выделяется при условии
 = e2
= e2 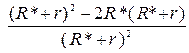 = 0.
= 0.
Отсюда следует: Р = Рm при R * = r. Тогда с учетом (3)
| Рm = e2 / 4 r , | (4) | ||
| Рm = n e12 / 4 r 1, | (5) |
Проверка формулы (5) на размерность:
[Рm ] = В2 / Ом = В × А = Дж× А / Кл = Дж / с = Вт.
Вычисления:
Рm = 3 × 1, 5 2 / ( 4 × 0, 30) = 5, 6 (Вт).
Ответ: Наибольшая мощность, которую можно получить от батареи Рm = 5, 6 Вт.
|
|
|




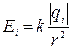 , i = 1, 2, 3, 4;
, i = 1, 2, 3, 4; 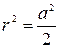 ,
,  . Отсюда следует: E = 2 E2,
. Отсюда следует: E = 2 E2, 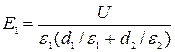 ;
; 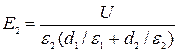
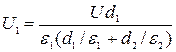 ;
; 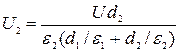
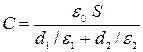 ;
;