Статистика носителей заряда в проводящих твердых телах

Калуга, 2009

УДК 537+539.2.

ББК 32.852.3

З-17

Настоящее методическое пособие издается в соответствии с учебным планом 7 семестра специальности 210104 «Микроэлектроника и твёрдотельная электроника»

Указания рассмотрены и одобрены:

Методической комиссией Калужского филиала МГТУ

им. Н.Э. Баумана, протокол № от

Председатель методической комиссии ______ А.В.Максимов

Методической комиссией факультета ЭИУК,

протокол № от

Председатель методической комиссии _______М.Ю. Адкин

Кафедрой "Материаловедение", протокол № от

Зав. кафедрой, профессор _____________В.Г. Косушкин

Рецензент: к.ф.-м.н, доцент

Автор: _____________ к.ф.-м.н, доцент В.С. Зайончковский,

Аннотация

Данное методическое пособие содержит описание основных положений и формул, необходимых для решения задач по дисциплине «Физика твердого тела».

© Калужский филиал МГТУ им. Н.Э. Баумана, 2009 г.

© Зайончковский В.С.

Содержание

№ пп	Содержание раздела	№ стр.
1.	Цель методического пособия
2.	Статистика носителей заряда в проводящих твердых телах
3.	Особенности расчета концентрации носителей заряда в полупроводниках с наличием основных и побочных минимумов энергетической зоны
4.	Дрейф носителей заряда
5.	Рекомбинация носителей заряда
6.	Диффузия носителей заряда
7.	Амбиполярная диффузия носителей заряда
8.	Диффузия и дрейф носителей заряда в магнитном поле
9.	Диффузия носителей заряда в магнитном поле
10.	Поглощение света в полупроводниках и диэлектриках
11.	Свойства диэлектриков
12.	Свойства сильных и слабых магнетиков
13.	Литература
	Приложение

Цель методического пособия

Целью данного методического пособия является оказание помощи студентам в решении задач по физике твердого тела. Содержание задач охватывает одиннадцать тем, теория по которым излагается в теоретическом курсе, читаемом в 6-ом и 7-ом семестрах для специальности «Микроэлектроника и твёрдотельная электроника».

Эти темы, в основном, описывают поведение однородных твердых тел, не содержащих разного рода границ – границ кристаллов, p-n переходов, изменений кристаллической и магнитной структур твердого тела.

Статистика носителей заряда в проводящих твердых телах

Статистика носителей заряда в твердых телах строится на основе зонной теории, которая разделяет все кристаллические твердые тела на металлы, полуметаллы, полупроводники, диэлектрики, в соответствии с концентрацией свободных носителей заряда. При большой концентрации носителей заряда распределение носителей заряда по энергии (вероятность заполнения состояний с энергией 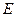) имеет вид функции Ферми-Дирака:

, (2-1)

где - энергия Ферми, - постоянная Больцмана, - абсолютная температура. Зависимость энергии в энергетической зоне является четной функцией от компонент волнового вектора электрона. Если в переносе заряда участвуют электроны с самых верхних, коллективизированных при образовании твердого тела, уровней, с одним главным квантовым числом, то в этом случае можно оценить число свободных электронов в единице объёма металла:

. (2-2)

Здесь - плотность металла, - атомная масса металла (масса атома металла в углеродных единицах), 1а.е.м. – масса одной атомной единицы массы, z- валентность металла, которая равна номеру группы в таблице Д.И. Менделеева, куда входит данный элемент, если конечно данный элемент входит в главную подгруппу. Но эта величина является верхней оценкой, т.к. в твердом теле величина z принимает меньшие и, довольно часто, дробные значения.

Для металлов с изотропной и параболической энергетической зоной из первой группы (главной подгруппы) таблицы Д.И. Менделеева В модели свободных электронов концентрация электронов связана с функцией распределения электронов по энергиям - функцией распределения Ферми- Дирака и энергия Ферми может быть определена из следующего соотношения:

. (2-3)

Здесь - плотность состояний в энергетической зоне. Для температуры абсолютного нуля соотношение (2-3) может быть преобразовано в следующее выражение:

, (2-4)

где - функция распределения Ферми- Дирака при температуре абсолютного нуля, - энергия Ферми для температуры абсолютного нуля. Эта формула используется для определения величины энергии Ферми для металлов с изотропными и параболическими энергетическими зонами. Результатом такого применения является соотношение:

. (2-5)

В этой формуле величины , - соответственно, концентрация электронов и функция распределения Ферми-Дирака, определяемые для температуры абсолютного нуля. Константа есть постоянная Планка, деленная на .

В металлах, входящих в длинные периоды таблицы

Д.И. Менделеева, возможно перекрытие подзон, наследованных от энергетических уровней с различными значениями главного квантового числа. В этом случае имеет место дробное (в среднем) число, коллективизированных от одного атома, электронов, участвующих в переносе заряда. При этом расчет концентрации свободных электронов является сложным. Если же:

· нет перекрытия подзон, с различными значениями главного квантового числа,

· зависимость энергии в зоне выражается квадратичной функцией от модуля волнового вектора,

· энергия отсчитывается от дна энергетической зоны,

· эта зона заполнена носителями заряда, так, что поверхность Ферми не касается границ зоны Бриллюэна,

то выражение для концентрации носителей заряда имеет вид:

. (2-6)

В этой формуле введены обозначения: - эффективная масса электрона, - нормированная энергия, отсчитанная от дна энергетической зоны, - приведенный уровень Ферми, отсчитанный от дна энергетической зоны. Аргумент подинтегрального выражения в формуле (2-6) равен:

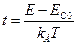. (2-7)

Приведенный уровень Ферми вычисляется по формуле:

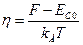. (2-8)

В формулах (2-7) и (2-8) величина представляет собой энергию дна данной энергетической зоны. Соотношение для расчета концентрации свободных электронов (формулу (2-3)) часто записывают в другом виде:

, (2-9)

Здесь - эффективная плотность состояний для зоны разрешенных энергий (зоны проводимости), - интеграл Ферми-Дирака. Эти сомножители описываются следующими соотношениями:

. (2-10)

. (2-11)

В соотношение (2-10) входит - константа для данного твердого тела – эффективная масса носителя заряда. Для интеграла Ферми-Дирака c индексом известны аппроксимации:

, при ; (2-12)

, при -1< h < 1.3; (2-13)

, при 1.3< h < 5; (2-14)

, при h > 5; (2-15)

Если выполняется двойное неравенство:

, (2-16)

то полупроводник можно охарактеризовать как невырожденный.

Если необходимо найти концентрацию носителей заряда вблизи потолка энергетической зоны (в валентной зоне), то в этом случае вместо выражения (2-9) используют ему подобное:

. (2-17)

Здесь введены новые обозначения: - концентрация носителей заряда с энергией вблизи потолка энергетической зоны (концентрация дырок), - ширина запрещенной зоны. Для дырок аппроксимации интеграла Ферми-Дирака остаются справедливыми с заменой аргумента на , с соответствующими модификациями неравенств при соотношениях (2-12) - (2-15). Если выполняется неравенство ,

то дырочный полупроводник можно охарактеризовать как невырожденный. Для невырожденных полупроводников справедлив закон действующих масс:

. (2-18)

Согласно этому закону произведение концентраций электронов и дырок в невырожденных полупроводниках зависит только от ширины запрещенной зоны и температуры полупроводника. Еще одна форма записи этого закона имеет вид:

, (2-19)

где введено обозначение

.

Величину называют собственной концентрацией носителей заряда. Вероятность заполнения состояния в энергетической зоне разрешенных энергий определяется соотношением (2-3). Вероятность нахождения носителей заряда на «мелких» примесных центрах в запрещенной зоне, если эти донорные центры имеют энергию , имеет вид:

. (2-20)

Такой вид это соотношение имеет при дополнительном условии, что не существует возбужденных примесных центров, и есть только один уровень энергии у примесного центра.

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: