Особенности расчета концентрации носителей заряда в полупроводниках с наличием основных и побочных минимумов зоны проводимости

Если энергии минимумов основной и побочной ветвей зоны проводимости близки (см. рис 1) и полупроводник невырожденный n-типа, то расчеты концентрации носителей заряда сводятся к использованию соответствующей аппроксимации интеграла Ферми-Дирака, см. соотношения (2-12) – (2-15). Если известно, что полупроводник невырожденный, то концентрации свободных электронов в основной и побочной долинах могут быть найдены модификацией соотношения (2-12):

, (3-1)

.(3-2)

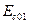Здесь и 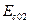- энергии основного и побочного минимумов (долин) зоны проводимости.

Пример решения Задачи

Задача 1

Исследуйте зависимость концентрации носителей заряда в побочном минимуме зоны проводимости арсенида галлия от температуры электронного газа. Суммарную концентрацию электронов считать независящей от температуры. Энергия дна побочного минимума больше энергии основного минимума зоны проводимости на . Полупроводник невырожденный n-типа.

Решение

Концентрация электронов в основном минимуме зоны проводимости равна:

Концентрация электронов в побочном минимуме зоны проводимости равна:

или

Т.к. имеется два типа носителей заряда – в основном и побочном минимумах зоны проводимости, то выражение для суммарной концентрации имеет вид:

Или

.

Ответ:

Дрейф носителей заряда

При наложении на проводящий образец внешнего электрического поля в образце возникает медленное, по сравнению с тепловым движением, направленное перемещение носителей заряда. Такой вид движения называют дрейфом. Вследствие такого движения появляется электрический ток. Вводят понятие дрейфовой скорости носителей заряда, которая представляет собой среднюю скорость направленного движения носителей заряда. Эта дрейфовая скорость для электронов определяется в соответствии с формулой:

, (4-1)

где - заряд электрона, взятый по модулю, - среднее время свободного пробега носителей заряда от столкновения до столкновения, - вектор напряженности внешнего электрического поля. Величина является результатом усреднения времени свободного пробега для одного электрона и усреднения этого времени для электронов с различной энергией. Введение среднего времени свободного пробега носителя заряда от столкновения до столкновения с ионами кристаллической решетки вводится после принятия двух предположений:

1) величина приобретаемой в поле энергии направленного движения носителя заряда много меньше энергии Ферми для металлов и много меньше тепловой энергии для полупроводников;

2) В момент столкновения с решеткой носитель заряда теряет всю энергию направленного движения.

Величину еще называют средним временем релаксации. За это время имеет место изменение в раз величины дрейфовой скорости после выключения внешнего электрического поля. Время релаксации зависит от механизмов рассеяния носителей заряда с потерей импульса и энергии. Известно, что существуют механизмы рассеяния носителей заряда на различных статических и динамических дефектах кристаллической решетки. Так возможно рассеяние на объёмных дефектах – включениях, плоских дефектах – границах зерен и малоугловых границах, линейных дефектах – дислокациях, точечных дефектах – межузельных атомах, примесных атомах в нейтральном и ионизованном состояниях. К динамическим дефектам кристаллической решетки относятся колебания кристаллической решетки. Суммарное время релаксации при наличии нескольких механизмов рассеяния следует формуле:

, (4-2)

Наиболее сильную температурную зависимость имеют механизмы рассеяния на примесных атомах и на колебаниях кристаллической решетки. Величина носит название подвижности носителей заряда и является величиной независимой от напряженности электрического поля для металлов и зависящей от него для полупроводников. Для почти заполненных энергетических зон можно ввести подвижность дырок:

.(4-3)

В металле газ свободных электронов следует статистике Ферми-Дирака. Средняя энергия свободных электронов в металле равна:

,

значит, средняя скорость хаотического движения электронов очень велика, и может достигать . Для всех температур, при которых металлы остаются твердыми телами, условие 1) автоматически выполняется.

В однородных твердых телах, при наличии одного сорта носителей заряда (электронов) плотность тока может быть связана с дрейфовой скоростью соотношением:

, (4-5)

Или с учетом соотношения (4-1):

. (4-6)

Множитель носит название удельной электропроводности.

После введения такого обозначения соотношение (4-6) получает вид:

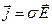. (4-7)

Это соотношение носит название закона Ома в дифференциальной форме.

В металлах концентрация носителей заряда есть величина, которую невозможно изменить, прикладывая к этим твердым телам электрические поля значительной интенсивности (даже такие, которые могут привести к плавлению металла). Кроме того, среднее время релаксации в металлах в твердом состоянии также не зависит от напряженности внешнего электрического поля. Поэтому , т.е. удельная электропроводность для металлов не есть функция от напряженности внешнего электрического поля. Закон Ома для постоянного тока соблюдается для всех возможных величин макроскопического электрического поля, которое можно реализовать в металлах в твердом состоянии!

В случае, если электрический ток переносится несколькими видами носителей заряда, то соотношение (4-1) следует изменить следующим образом:

, (4-8)

где , и - заряд, концентрация и скорость дрейфа соответствующего -го вида свободных носителей заряда. Если же выполняется закон Ома, то в этом случае соотношение (4-8) будет иметь вид:

. (4-9)

В однородных полупроводниках закон Ома может не соблюдаться так, как концентрация и скорость дрейфа носителей заряда могут изменяться в зависимости от величины напряженности электрического поля. И тогда для расчета плотности тока надо применять не соотношение (4-6), а соотношение (4-5). Рассеяние носителей заряда при их движении под действием электрического поля приводит к выделению тепла, которое для единицы объема в единицу времени описывается законом Джоуля-Ленца в дифференциальной форме:

. (4-10)

Задача 5

Определите подвижность электронов в алюминии, имеющем удельное сопротивление 2.8*10^-6 Ом*см и плотность 2.7 г/см³. Атомная масса алюминия, взятая в атомных единицах массы, равна 27. Из трех валентных электронов атома алюминия в кристаллическом алюминии в среднем электрона свободны (первая зона Бриллюэна, при рассмотрении в представлении расширенных зон, полностью заполнена) и могут принять участие в процессе проводимости. Считая, что m_эфф =m_о, найдите среднее время между соударениями и сравните это значение с соответствующим значением для слаболегированного кремния.

Решение

Удельное сопротивление при наличии одного типа носителей заряда следует формуле:

.

Концентрация свободных электронов, учитывая примечание в условии, может быть найдена следующим образом:

. Комбинация этих двух формул позволяет найти значение подвижности носителей заряда. Подвижность носителей заряда связана со временем релаксации (средним временем свободного пробега носителей заряда) посредством следующего соотношения:

.

Ответ , .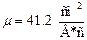

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: