Свойства сильных и слабых магнетиков

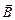Энергия магнитного момента в поле с магнитной индукцией описывается формулой:

. (12-1)

Намагниченность насыщения (величина суммарного магнитного дипольного момента) определяется, как:

. (12-2)

Здесь - элемент объема, в котором находятся магнитные дипольные моменты.

Индукция постоянного локального магнитного поля представляется в виде суммы нескольких компонент:

, (12-3)

Макроскопическое поле в магнетике описывается формулой:

, (12-4)

Здесь Гн/м - магнитная проницаемость вакуума, - напряженность магнитного поля, создаваемая сторонними источниками. Выражение (12-4) может быть переписано в другом виде:

, (12-5)

где - тензор магнитной проницаемости для сильных магнетиков, и скаляр - для слабых магнетиков. К слабым магнетикам относятся диа- и парамагнетики. Остальные виды магнетиков относятся к сильным магнетикам. Физический смысл напряженности магнитного поля состоит в том, что выполняется соотношение:

. (12-6)

В этом выражении 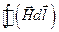- циркуляция вектора напряженности магнитного поля по контуру, пронизывающему обмотку электромагнита равна магнитодвижущей силе, т.е. произведению величины электрического тока , протекающего по обмотке электромагнита, на число витков провода в этой обмотке.

Внешнее по отношению к конкретному атому или иону магнитное поле приводит к поляризации этого атома или иона и к появлению явления диамагнетизма. Явление диамагнетизма может проявляться и при поляризации движения свободных носителей заряда в твердом теле – явления диамагнетизма Ландау. При отсутствии не полностью заполненных электронных оболочек атомов или ионов, и в случае, если энергия возбуждения велика по сравнению с энергией спинового магнитного момента в данном магнитном поле, а также в случае отсутствия свободных носителей заряда реализуется слабое явление диамагнетизма, не маскируемого явлениями парамагнетизма и ферромагнетизма. При этом величина относительной магнитной проницаемости является скаляром, определяемым по формуле:

, (12-7)

и связана с величиной магнитной восприимчивости следующим образом:

. (12-8)

В этом случае диамагнитная восприимчивость равна:

. (12-9)

Здесь - полное число электронов в данной оболочке атома со средним квадратом радиуса электронного облака , - концентрация атомов в твердом теле. Эта формула справедлива, если в нашем твердом теле один сорт атомов. В ином случае необходимо суммировать по всем сортам атомов.

Если же, как и в случае диамагнетизма при отсутствии не полностью заполненных электронных оболочек атомов или ионов магнитное поле переводит электроны в атоме или ионе в возбужденные состояния, то реализуется явление носящее название поляризационного парамагнетизма или парамагнетизма Ван Флека.

При наличии парамагнитных ионов или атомов, имеющих магнитный момент в отсутствие внешнего магнитного поля, имеет место ориентационный парамагнетизм Ланжевена (в классической трактовке) и парамагнетизм Бриллюэна при квантовой трактовке. При этом величина модуля дипольного момента не зависит от величины локального магнитного поля. В случае ориентационного парамагнетизма влияние магнитного поля проявляется только в ориентации дипольных моментов и появлении зависящего от этого поля вектора намагниченности. При снятии внешнего магнитного поля тепловое движение приводит к хаотической ориентации дипольных моментов атомов, ионов или молекул - частиц твердого тела. Если не учитывать квантовых особенностей такого вида поляризации, состоящих в том, что углы разориентации дипольных моментов относительно выбранного направления (направления внешнего магнитного поля являются набором дискретных значений, то можно считать, что угол разориентации дипольного момента относительно выбранного направления может обладать непрерывным набором значений от 0 до 180 градусов. При этом среднее значение косинуса угла разориентации одного сорта дипольного момента подчиняется формуле Ланжевена:

, (11-10)

где . (11-11)

Если в твердом теле есть только один сорт частиц обладающих таким видом поляризации, то модуль вектора поляризации определяется выражением:

. (11-12)

Это соотношение при высоких температурах (т.е. при выполнении следующего неравенства):

):

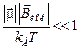приводит к выполнению закона Кюри (определенной зависимости парамагнитной восприимчивости от температуры):

. (11-13)

Если данное твердое тело при снижении температуры может перейти из парамагнитного состояния в ферро- или ферримагнитное, то формула (11-13) должна быть модифицирована. В этом случае выполняется закон Кюри-Вейсса, согласно которому:

, (11-14)

где - носит название температуры Кюри.

Третьим видом парамагнетизма является парамагнетизм свободных электронов – носящий название парамагнетизма Паули. В этом случае магнитная восприимчивость практически не зависит от температуры.

Ферромагнетизм присущ только твердому телу, хотя возможен и в аморфном состоянии. В твердых телах, в которых при высоких температурах реализуется парамагнетизм Ланжевена (Бриллюэна) в области низких температур обменная энергия электронов соседних атомов может превзойти энергию теплового движения магнитных моментов. В этом случае реализуется ферро- или ферримагнитное состояние. В жидкости ферромагнитное состояние не реализовано. В Википедии — свободной энциклопедии - можно прочитать: «Несмотря на название, ферромагнитные жидкости не проявляют ферромагнитных свойств, поскольку не сохраняют остаточной намагниченности после исчезновения внешнего магнитного поля. На самом деле ферромагнитные жидкости являются парамагнетиками и их часто называют «суперпарамагнетиками» из-за высокой магнитной восприимчивости». Фактически ферромагнитные жидкости представляют собой суспензию малых (твердотельных) ферромагнитных частиц в связующей жидкости.

В ферромагнетиках в слабых полях имеет место разбиение объема образца на области с определенной ориентацией намагниченности, называемыми доменами. В 1935 г. Ландау и Лифшиц определили, что эти домены разделены переходными областями – названными доменными границами (доменными стенками). Эти особенности в ферромагнетиках произошли вследствие наличия нескольких вкладов в полную энергию ферромагнетика, таких как: обменная энергия, энергия магнитной анизотропии, магнитостатическая энергия, энергия Зеемана, магнитоупругая энергия.

Обменная энергия обусловлена перекрытием электронных облаков соседних атомов или ионов. Эта энергия описывается моделью Гейзенберга:

, (12-15)

где - обменный интеграл, - спин 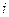-го атома, суммирование идет по всем атомам или ионам, находящимся в единице объёма, исключая повторяющиеся пары. Состояние с одинаковым направлением спинов в твердом теле соответствует однородной намагниченности и минимуму обменной энергии.

Энергия кристаллографической и (или) наведенной анизотропии – обусловлена анизотропией в перекрытиях электронных оболочек атомов. В случае появления одноосной анизотропии этот вклад в полную энергию единицы объема описывается формулой:

, (12-16)

где - угол между намагниченностью и главной осью этого ферромагнетика, и , соответственно, первая и вторая константы одноосной анизотропии, зависящие от температуры. Обычно выполняется соотношение:

(12-17)

В случае кубической анизотропии вклад в полную энергию описывается формулой:

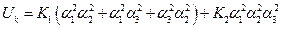, (12-18)

где - косинусы углов между направлением намагниченности и ортами прямоугольной системы координат. При этом также .

Магнитостатическая энергия, которую еще называют энергией размагничивания, является энергией полей рассеяния магнитных полюсов, сформированных в твердом теле. Наиболее просто этот вклад в энергию ферромагнитного тела рассчитывается при однородном намагничивании твердого тела правильной формы. Правильной формой называют форму тела, при которой касательная плоскость к любой точке поверхности твердого тела в тоже время не является секущей плоскостью в других точках этого твердого тела. Формула для магнитостатической энергии единицы объема имеет вид:

,(12-19)

где - размагничивающий фактор. Энергия Зеемана – энергия единицы объема магнитного образца в поле, создаваемом внешними источниками магнитного поля. Выражение для энергии Зеемана для единицы объема следует формуле:

. (12-20)

Магнитоупругая энергия имеет два слагаемых – одно связано с деформацией тела при его намагничивании, второе - связанно с деформацией этого тела под действием приложенных внешних, по отношению к данному твердому телу, сил. При наличии деформаций описываемых тензором , приводящих к ненулевому тензору механических напряжения , магнитоупругая энергия единицы объема магнитного образца выражается в виде:

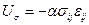.(12-21)

Здесь, в соответствии с правилом Ландау, имеет место суммирование по повторяющимся индексам, а сами индексы пробегают значения 1, 2 и 3. Так как, согласно работе Ландау и Лифшица 1935 года, намагниченность в доменах однородна, то обменная энергия внутри домена минимальна. Обменная энергия очень велика в доменных границах. Поэтому магнитную структуру ферромагнетика рассматривают следующим образом: находят энергию доменных стенок и затем уже определяют энергию доменной структуры, с одновременным нахождением доменной картины.

Структура доменных стенок определяется в основном обменной энергией, энергией анизотропии и магнитостатической энергией. Доменными стенками, имеющими простейшие структуры ориентации спинов, являются стенки Блоха и стенки Нееля. В первом случае вектор магнитного момента при трансляции на один период магнитной решетки вращается вокруг оси перпендикулярной плоскости стенки, а во втором случае имеет место вращение вокруг оси, лежащей в плоскости стенки. В наиболее простом случае полный разворот магнитного момента от одного домена к другому составляет . В этом случае такую доменную стенку называют -ой. Они реализуются при наличии одноосного характера магнитной анизотропии с положительным значением первой константы - т.е. в варианте вида анизотропии типа «легкая ось». В случае стенок Блоха, при большой толщине образца, энергия размагничивания равна нулю. И поэтому толщину доменной стенки 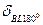и ее энергию (точнее энергию, приходящуюся на единицу поверхности доменной стенки ), можно найти, учитывая только обменную энергию и энергию магнитной анизотропии.

. (12-22)

. (12-23)

В эти формулы введено обозначение для величины обменного параметра:

, (12-24)

 

где - обменный интеграл, - модуль механического момента спина электрона, - параметр магнитной решетки. В толстых пленках и массивных образцах реализуются стенки Блоховского типа. Для тонких пленок полная энергия доменной стенки Неелевского типа становится меньше, чем аналогичная величина для стенки Блоховского типа. Когда эти энергии сравнимы по величине, то возможно сосуществование двух этих типов в одной доменной стенке и тогда появляются переходные области, носящие название Блоховских линий.

Доменные структуры бывают открытого и закрытого типов. У первых имеет место замкнутая доменная структура. И тогда энергия магнитостатическая – энергия полей рассеяния равна нулю. При расчетах таких структур принимают во внимание только энергию доменных стенок и энергию анизотропии (если конечно отсутствуют внешние источники магнитных полей). Равновесная толщина доменов в теле ферромагнетика равна

.(12-25)

Здесь - толщина пленки или пластины, и, кроме того, - гипотенуза равнобедренного треугольника, лежащего в основании прямой призмы – замыкающего домена. Энергия, приходящаяся на единицу площади поверхности пластины, равна:

.(12-26)

Для открытой доменной структуры равновесная ширина домена, если конечно отсутствуют внешние источники магнитных полей, равна:

,(12-27)

а энергия, приходящаяся на единицу площади поверхности пластины, равна:

. (12-20)

 

Литература

1. Павлов П.В., Хохлов А.Ф. Физика твердого тела, -М., Высшая школа, 2000 г.

2. Ашкрофт Н., Мермин Н. Физика твердого тела, -М., Мир, 1989 г.

3. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред, -М., Высшая школа, 1976 г.

4. Бонч-Бруевич В.Л., Калашников С.Г. Физика полупроводников,

5. -М., Наука, 1990 г.

6. Киттель Ч. Введение в физику твёрдого тела, - М., Наука, 1990 г.

7. Оптические свойства полупроводников, - под ред.

Р. Уиллардсона и Ф. Бира, -М., Мир, 1975 г.

8. Чеченин Н.Г. Введение в физику твердого тела, лекции,

http://nuclphys.sinp.msu.ru/solidst/

Приложение 1

Фундаментальные физические постоянные [ ]

Постоянная	Обозначение	Числовое значение
Скорость света в вакууме	С
Постоянная Планка
Нормированная постоянная Планка
Магнитная постоянная
Электрическая постоянная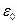
Масса покоя электрона
Заряд электрона (абс. величина)
Магнетон Бора
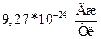
Атомная единица массы	а.е.м.
Постоянная Авогадро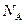
Молярная газовая постоянная
Постоянная Больцмана
Радиус первой боровской орбиты

 

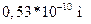
Приложение 2

Учебные задачи к дисциплине «Физика твердого тела». При решении задач можно пользоваться приложениями 1, 3 и 4.

1. Статистика носителей заряда в металлах

Задача 1

Определите, как изменится вероятность заполнения энергетического уровня, расположенного на 0.1 эВ выше и ниже уровня Ферми при повышении температуры от до [1]

Задача 2

Определите минимальную длину волны де Бройля для свободных электронов при в металле – натрии с объемно центрированной кубической кристаллической решеткой, если на каждый атом кристалла металла приходится один свободный электрон. Период решетки равен , массу электрона в кристалле принять равной массе свободного электрона,

Задача 3

Определите энергию Ферми для лития, натрия, калия и цезия. Объясните, почему она уменьшается с увеличением атомного номера элемента.

Задача 4

Определите эффективную массу носителей заряда в литии, если известно из эксперимента, что максимальная энергия электронов проводимости в кристалле лития составляет 4,2 эВ. Полагая при этом, что на каждый атом кристаллической решетки приходится один свободный электрон. Плотность лития принять равной .

Задача 5

Вычислите концентрацию свободных электронов в меди, если известно, что плотность меди . При расчете надо полагать, что на каждый атом кристаллической решетки приходится один электрон.

Задача 6

Положение уровня Ферми для алюминия при температуре соответствует энергии 11, 7 эВ. Рассчитать число свободных электронов, приходящихся на один атом. Эффективную массу электронов проводимости принять равной массе свободного электрона.

Задача 7

Вычислите, какая часть электронов проводимости в простом металле при температуре имеет кинетическую энергию, большую .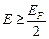

 

2. Статистика носителей заряда в полупроводниках

Задача 1

Найдите положение уровня Ферми и температурную зависимость концентрации электронов в собственном полупроводнике для невырожденного случая. Как изменится концентрация электронов в собственном кремнии при изменении температуры от 200К до 300К.

Задача 2

Вычислите собственную концентрацию электронов в германии и кремнии при температуре 300К. Эффективные массы плотности состояний в валентной зоне принять равными 0.362 для германия и 0.595 для кремния (в долях от массы свободного электрона). Ширина запрещенной зоны составляет 0.66 эВ для германия и 1.12 эВ для кремния.

Задача 3

Вычислите удельную электропроводность чистых германия и кремния при Т=300 К. Подвижность носителей принять равной:

для германия m_n = 3900 см²/В*с; m_p = 1900 см²/В*с.

для кремния m_n = =1417 см²/В*с; m_p =47 см²/В*с.

Задача 4

В зоне проводимости арсенида галлия наряду с основным минимумом, лежащим в центре зоны Бриллюэна, имеются побочные минимумы, расположенные на DЕ=0.31 эВ выше основного. Исследовать концентрационную зависимость уровня Ферми в таком полупроводнике для невырожденного электронного газа. Влиянием остальных зон пренебречь.

Задача 6

Рассчитайте зависимость населенности верхних минимумов арсенида галлия от температуры электронного газа в отсутствие вырождения. Чему равно отношение концентрации электронов в верхнем минимуме к концентрации электронов в основном минимуме при Т=300К. Эффективную массу плотности состояний для электронов в верхнем минимуме принять равной m_n2/m₀= 15, где. m₀ – масса свободного электрона.

Задача 7^*

Найдите связь концентрации электронов с уровнем Ферми в полупроводниках, если известно, что при малых значениях величины квазиволнового вектора К электрона закон дисперсии имеет вид:

E=(1-aK²)ħ²K²/2m_эфф

где а - постоянная величина, m_эфф - эффективная масса электрона у дна зоны проводимости.

Задача 8

Исследуйте температурный ход уровня Ферми в примесной области для невырожденного полупроводника, содержащего один тип мелких доноров с концентрацией N_t. Возбужденными состояниями донорных атомов пренебречь.

Задача 9

Известно, что кристалл кремния в качестве легирующей примеси содержит 10^-4 атомных процента мышьяка Аs. Затем он равномерно легируется бором и полученная концентрация атомов примеси составляет 3*10¹⁸ aтом/см³ бора. Вслед за этим термический отжиг полностью активирует атомы примеси (атомы примеси встраиваются в узлы кристаллической решетки). Образец находится при температуре, при которой все примесные атомы ионизованы. Плотность монокристаллического кремния равна 2.328 г/см³.

а) Чему будет равна концентрация основных примесей?

б) Какой тип проводимости будет иметь образец кремния?

в) Какова концентрация и тип свободных носителей заряда?

Задача 10

Найдите равновесную концентрацию электронов и дырок, а также положение уровня Ферми (по отношению к собственному уровню Ферми F) в кремнии при 300^оС, если кремний содержит 8*10¹⁶ см ^-3 атомов мышьяка (Аs) и 2*10¹⁶ см ^-3 атомов бора (В).

Задача 11

В образец GaAs вводятся атомы кремния. Кремний может заместить атомы трехвалентного галлия или пятивалентного мышьяка. Предположим, что атомы кремния действуют как полностью ионизированные атомы легирующей примеси и что 5% из введенных 10¹⁵ см^-3 атомов кремния замещают атомы галлия, а 95% замещают атомы мышьяка. Температура образца 300 К.

а) рассчитайте концентрации доноров и акцепторов.

б) определите концентрации электронов и дырок и положение уровня Ферми.

Задача 12

Один образец кремния n-типа имеет равномерную концентрацию Nd= 10¹⁶ cм^-3 атомов мышьяка, а другой образец кремния р-типа имеет Nа=10¹⁵ см^-3 атомов бора. Для каждого полупроводникового материала определите:

а) температуру, при которой ионизирована половина примесных атомов. Предполагается, что все подвижные электроны и дырки поступают от легирующих примесей.

б) температуру, при которой собственная концентрация n превосходит концентрацию примесей в 10 раз.

в) равновесную концентрацию неосновных носителей заряда.

Предполагается, что все примеси ионизованы.

г) положение уровня Ферми относительно края валентной зоны в каждом материале при 300 К.

д) положение уровня Ферми относительно края зоны проводимости, если оба типа примеси имеются в одном образце.

Параметры кремния даны в таблице 1

Постоянная решетки	Ширина запрещённой зоны	Собственная концентрация электронов приТ=300K	Еа -Еvо, Бор	Есо -Еd, Мышьяк
0.54307 нм	1.124 эВ	n = 1.4*1010см-3	0.045 эВ	0.049 эВ

3. Электропроводность металлов и сплавов

Задача 1

Что называют температурным коэффициентом удельного сопротивления? Является ли он константой для данного материала?

Задача 2

Как влияют примеси на удельное сопротивление металлов? Сформулируйте правило Маттисена.

Задача 3

Почему металлические сплавы типа твердых растворов обладают более высоким удельным сопротивлением, чем чистые компоненты, образующие сплав?

Задача 4

Как и почему меняется сопротивление металлов при плавлении?

Задача 5

Вычислите длину свободного пробега электронов в меди при , если удельное сопротивление при этой температуре равно мкОм*см. Считать, что форма поверхности Ферми для меди - сферическая.

Задача 6

По медному проводнику с площадью поперечного сечения 0.2 мм² протекает ток силой 1А. Плотность меди равна 8.89 г/см³, а её атомный вес 63.5. Какова средняя скорость дрейфа электронов? Считайте, что один атом меди отдает в море свободных электронов один электрон.

Задача 7

Определите максимальную частоту тепловых колебаний атомов в кристаллах алюминия, для которого температура Дебая равна . Какую энергию будет иметь фотон с эквивалентной энергией?

Задача 8

В медном проводнике под действием электрического поля проходит электрический ток плотностью 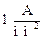. Определите скорость дрейфа и отношение ее к средней суммарной скорости движения электронов при .

4. Электропроводность полупроводников

Задача 1

Образец слаболегированного кремния n-типа имеет (при 27^оС) удельное сопротивление 5 Ом*см. Найдите концентрацию дырок при 27^оС, 100^оС и 500^оС в условиях теплового равновесия.

Задача 2

Однородный образец кремния n-типа подключили к источнику питания. При этом через образец стал протекать ток определенного значения. После этого увеличили в два раза напряжение, приложенное к этому образцу. После этого ток возрос только на 50%. Объясните это явление. Кремний остается нейтральным при обоих значениях силы тока.

Задача 3.

В образце полупроводника действуют два механизма рассеяния носителей заряда. Если бы действовал только первый механизм рассеяния, то подвижность носителей заряда была бы равна 800 см²/В*с. Если бы действовал только второй механизм, то подвижность этих носителей была бы равна 200 см²/В*с. Чему равна подвижность с учетом двух механизмов?

 

5. Рекомбинация и релаксация носителей заряда

Задача 1

В момент времени t = 10 ^{– 4} с после выключения равномерной по объему генерации электронно-дырочных пар неравновесная концентрация носителей оказалась в 10 раз больше, чем в момент t = 10 ^-3 с. Определите время жизни t, если уровень возбуждения невелик и рекомбинация идет через простые дефекты.

Задача 2

При слабом освещении в полупроводнике генерируются пары носителей заряда, при этом время жизни оказалось равным t мкс. Скорость объемной рекомбинации – γ. Определите равновесные концентрации n_o и p_o, если известна температура опыта, а также Eg, m_n, m_p и полупроводник невырожденный.

Задача 3

При биполярной генерации в примесном полупроводнике скорость объемной рекомбинации - γ и время жизни носителей заряда - t. Отношение времени жизни электрона примесного полупроводника к времени жизни его в собственном полупроводнике составило 0.1. Определите ширину запрещенной зоны полупроводника при температуре эксперимента 300К, если известно, что отношение масс электрона и дырки к массе свободного электрона составило 0.07 и 0.40, соответственно. Влияние дефектов структуры на время жизни в этом образце полупроводника не существенно. Полупроводник невырожденный.

 

6. Диффузия носителей заряда в полупроводниках

Задача 1

Определите коэффициент диффузии электронов в сильно легированном полупроводнике n-типа. Для интеграла Ферми принять аппроксимацию:

Задача 2

В однородный полубесконечный электронный полупроводник (х >0) стационарно инжектируются дырки, так что избыточная концентрация в плоскости х=0 равна: Dp (0) = 10¹⁴ cм^-3. Определите неравновесную концентрацию дырок на расстоянии х = 0.4 см от поверхности. Время жизни дырок равно: t_p =10 ^-3 с. Температура образца (слабо легированного арсенида галлия (GaAs)) - равна 300 К.

Задача 3

В однородный полубесконечный полупроводник (кремний) расположенный в области (х>0) при х=0 стационарно инжектируются дырки. Определите концентрацию введенных дырок при х=0, если коэффициент инжекции x= j_p / (j _n + j _р) = 0.5. Полная плотность тока при этом равна j = 1.6 мА /см ². Длина диффузии дырок равна 0.1 см, температура эксперимента 300 К.

Задача 4

Вычислите коэффициент амбиполярной диффузии для собственного полупроводника (германия), если отношение подвижностей носителей заряда m_n /m_p = 2.1;

m_n = 3800 см²/ В*с.

Задача 5

В некоторой точке однородного электронного полупроводника световым зондом генерируются носители заряда. Считая задачу одномерной, определите диффузионную длину неравновесных носителей заряда, если концентрация этих носителей заряда на расстоянии х =2 мм от зонда равна Dр = 10 ⁵ см^-3, а при х = 4.3 мм - Dр = 10 ³ см^-3.

 

7. Дрейф и диффузия носителей заряда в магнитном поле

Задача 1

В образце n-типа плотность тока вдоль оси X равна j = 0.1 A/cм². Магнитное поле направлено по оси Z и равно B=0.1Тл. В условиях рассеяния электронов на колебаниях кристаллической решетки r_H=1.18. Определите Rн и холловское напряжение, если n = 10¹⁵ см^-3 и размер образца в направлении оси Y равен 0.5 см.

Задача N2

При наложении на образец полупроводника n-типа магнитного поля с индукцией В=0.4Тл, перпендикулярной направлению тока, проводимость уменьшилась на 3*10^-3 Ом^-1*см^-1. Определите коэффициент магнетосопротивления, если энергия ионизации мелких доноров равна 0.005 эВ, а концентрация их – N_d=10¹⁶ см^-3. Время релаксации импульса равно 10^-9 с, зоны параболические, E_со - F = 5kT, отношение массы электрона в решетке к массе свободного электрона равно 1/ 2.

Задача 3

Определите постоянную Холла в InSb, содержащем акцепторы с концентрацией p=5*10¹⁶ cм^-3, если r=1.18, b= 80. Магнитное поле слабое, собственная концентрация электронов n_i=10¹⁶ см^-3, акцепторы полностью ионизованы.

Задача 4

Образец полупроводника n-типа при 100К имеет коэффициент Холла

R_H=0.28*10^-2 м³/Кул. Определите плотности электронов и доноров, если материал – кремний, а энергия ионизации мелких доноров может быть принята равной 0.04 эВ.

Задача 5

Какова должна быть концентрация акцепторов в кремнии р-типа, чтобы при комнатной температуре величина эффекта Холла была равна нулю. Считайте, что величины времени релаксации импульса не зависят от концентрации носителей заряда.

ЗадачаN6

Эффект Кикоина-Носкова (ФЭМ-эффект)

 

8. Оптика полупроводников

Задача 1

При отражении света толстым полупроводниковым образцом (с толщиной, равной l=100 мкм) коэффициент отражения оказался равным R = 0.36. Коэффициент пропускания пленки из того же материала толщиной t = 1 мм равен T = 0.17. Вычислите коэффициент поглощения a. Многопроходность света учесть, а интерференцией света пренебречь.

Задача 2

Определите величины квазиволновых векторов электрона и дырки, рождаемых при поглощении кванта света в прямозонном полупроводнике с параболическими изотропными законами дисперсии. Принять Еg = 0.3 эВ, эффективные массы электрона и дырки – m_n= m_p =0.4 m₀, длина волны кванта света в вакууме равна 4 мкм, импульсом кванта света в первом приближении пренебречь, во втором - использовать тот факт, что показатель преломления равен 4.0.

Задача 3

Определите избыточную проводимость арсенида галлия, если известно, что на поверхность тонкого образца полупроводника падает луч света с интенсивностью I. Что для этого надо знать?

Задача 4

Определите максимально возможную величину фотоэдс эффекта Дембера, если показатель преломления полупроводника равен 4, материал - собственный Gе, длина волны l = 1.55 мкм, показатель поглощения k = 0.1, интенсивность потока квантов света I_кв = 10¹⁵ квантов/см², квантовая эффективность равна h = 1.

Задача 5

Рассчитайте максимально возможную длину электромагнитной волны, вызывающую рождение электронно-дырочных пар в собственном германии, кремнии, арсениде галлия и SiO₂. Идентифицировать вид электронного перехода для каждого случая.

Задача63

Вычислите относительное изменение проводимости примесного полупроводника при стационарном освещении с интенсивностью I = 5*10 ¹⁵ квантов/см² за одну секунду. Коэффициент поглощения принять равным a = 100 см ^-1. Толщина образца L << 1/a. Рекомбинация идет на простых дефектах. Равновесная концентрация электронов n = 10¹⁵ см^-3, время жизни электронов t= 10^-4 с. Отношение подвижности электрона к подвижности дырки равно b = 20, квантовая эффективность процесса рождения электронно- дырочных пар равна единице (h = 1).

 

9. Свойства диэлектриков и магнитные явления в твердом теле

Задача 1

Вычислите средний угол ориентации классических электрических дипольных моментов относительно направления внутреннего электрического поля диэлектрика при величине отношения dE/kT равном 0.1.

Задача 2

Определите эффективное магнитное поле в ферромагнетике, имеющем форму шара. Образец имеет магнитоодноосную анизотропию типа «легкая ось».

Задача 3

Определите равновесные значения ширины доменов (с ориентацией параллельно вектору индукции В₀₎ в одноосном ферромагнетике, находящемся в магнитном поле с индукцией В₀, ориентированной вдоль легкой оси ферромагнетика. Считать, что число доменов не отличается от величины числа доменов при условии равенства нулю индукции внешнего магнитного поля В₀. Доменная структура – открытая (т.е. в ферромагнетике существуют 180⁰- доменные границы).

 

Приложение 3

ТАБЛИЦА N1

Тип кристаллической решетки	О.Ц.К Ц. К.	О.Ц.К	О.Ц.К.	О.Ц.К.	О.Ц.К.	Г.П.У.	Г.П.У.	Г.Ц.К	Г.Ц.К	О.Ц. К	Г.Ц.К	Тетрагон. Призм.	ГПУ
Параметр кристаллической решетки, a, нм	0.35	0.43	0.52	0.56	0.61	0.23	0.32	0.56	0.6	0.50	0.40

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: