 |
Диффузия носителей заряда в магнитном поле
|
|
|
|
Примером реализации диффузии носителей заряда в магнитном поле является фотоэлектромагнитный эффект (ФЭМ - эффект), который называют еще эффектом Киккоина-Носкова. Этот эффект наблюдают в пластинах полупроводников освещаемых светом, который генерирует в полупроводнике носители заряда с положительным и отрицательным знаком заряда. Пластина полупроводника (поверхность перпендикулярна направлению Z) должна находиться в магнитном поле, лежащем в плоскости пластины (пусть это направление Х). В направлении Z (вглубь полупроводника) имеет место диффузия неравновесных носителей заряда двух знаков. Магнитное поле разделяет носители заряда в направлении Y. Если эти две грани образца замкнуть через амперметр с малым внутренним сопротивлением, то ток короткого замыкания 
будет равен:
. (9-1)
В этом соотношении 
- заряд электрона, взятый по модулю, 
- число квантов света, поглощаемых в единицу времени единицей поверхности полупроводника, 
- модуль индукции магнитного поля, 
- коэффициент пропорциональности, зависящий только от свойств полупроводника, в том числе и от времени жизни носителей заряда.
Поглощение света в полупроводниках и диэлектриках
При падении света на металл имеет место эффективное отражение света, связанное с большой концентрацией носителей заряда в металлах.
При поглощении света полупроводниками и диэлектриками имеет место возбуждение неравновесных носителей заряда.
Поглощение света с определенной длиной волны в пластине толщиной 
при пренебрежении интерференционными эффектами описывается модифицированной формулой Бугера-Ламберта-Бэра:
. (10-1)
В этой формуле 
- коэффициент отражения света поверхностью пластины, 
- коэффициент поглощения света. Известно несколько механизмов поглощения света в полупроводниках и диэлектриках. При этом должны выполняться законы сохранения энергии и импульса в элементарных процессах поглощения кванта света. Так, например при «собственном» механизме поглощения света энергия кванта света 
расходуется на вырывание электрона из валентной зоны (т.е. на генерацию двух носителей заряда – свободных электрона и дырки), сообщению электрону и дырки определенной кинетической энергии, а также на рождение или уничтожение кванта колебаний кристаллической решетки (фонона).
|
|
|
. (10-2)
Здесь 
- квадрат модуля волнового вектора электрона, 
- квадрат модуля волнового вектора дырки, 
- энергия фонона. При прямых переходах электрона из валентной зоны в зону проводимости, что чаще происходит в прямозонных полупроводниках, фононы не возбуждаются. Кроме закона сохранения энергии (выражение (10-2)), выполняется закон сохранения импульса:
. (10-3)
В левой стороне этого выражения стоит импульс фотона, а в правой стороне выражения первое слагаемое – импульс электрона, второе – импульс дырки, третье – импульс фонона. В выражение (10-3) введены обозначения 
- скорость света в твердом теле, 
- скорость звука в твердом теле, 
- единичный вектор в направлении распространения фотона в твердом теле, 
- единичный вектор в направлении распространения фонона в твердом теле. Верхний знак в правых сторонах выражений (10-2) и (10-3) используется при рождении фонона, нижний – при уничтожении фонона. Если же кристаллическая решетка не участвует в рождении пары электрон- дырка, то последнее слагаемое в этих выражениях отсутствует.
Свойства диэлектриков
Специфические свойства диэлектриков по сравнению с полупроводниками проявляются не только в том, что они обладают значительно большим удельным сопротивлением, но и в том, что в этих твердых телах сильнее могут проявляться процессы, связанные с поляризацией вещества во внешних электрических полях. Диэлектрики могут менять свое поляризованное состояние под действием механического воздействия и при изменении температуры твердого тела, и, кроме того, разные области одного и того же твердого тела могут быть по-разному поляризованы. Известны 4 вида поляризации:
|
|
|
· упругая:
· ориентационная,
· сегнетоэлектрическая;
· миграционная.
Дипольный момент атома или иона 
при упругой поляризации определяется по формуле:
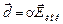. (11-1)
Здесь 
- локальное электрическое поле в месте расположения атома или иона, - коэффициент пропорциональности, носящий название коэффициента поляризуемости. Размерность этого коэффициента: 
.
Его не надо путать с термином поляризация (состояния, когда тело или часть его обладают преимущественным направлением ориентации дипольных моментов) и с вектором поляризации, определяемым как:
. (11-2)
Размерность вектора поляризации:
.
При ориентационной поляризации диэлектрика молекулы обладают дипольным моментом в отсутствие внешнего электрического поля, причем внешнее электрическое поле не изменяет модуля вектора дипольного момента индивидуальных молекул, но оказывает ориентирующее действие на них.
При сегнетоэлектрической поляризации поляризованными являются относительно большие объемы твердого тела в отсутствие внешнего электрического поля, при этом объем тела разбит на части (домены) – области с определенным значением и ориентацией вектора поляризации. У всех доменов данного однородного (по составу) тела модуль вектора поляризации является величиной постоянной. Сегнетоэлектрическая поляризация связана с возможностью небольшого искажения кристаллической решетки в некоторых направлениях, причем появляющийся дипольный момент данной элементарной ячейки индуцирует аналогичное искажение кристаллической решетки в соседних кристаллических ячейках.
Энергия 
дипольного момента в локальном электрическом поле дается формулой:
. (11-3)
Локальное электрическое поле представляется в виде суммы нескольких компонент:
, (11-4)
где в правой части, соответственно, 
– поле внешних источников, 
- деполяризующее поле, 
- поле полости Лоренца,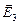 
- поле диполей, находящихся в сфере Лоренца.
|
|
|
Индукция электрического поля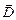 
в неактивном диэлектрике описывается формулой:
. (11-5)
Здесь 
- диэлектрическая проницаемость вакуума, 
(11-7)
- макроскопическое электрическое поле, 
- вектор наведенной поляризации диэлектрика.
Размерность модуля вектора 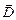совпадает с размерностью модуля вектора , т.е. 
.
Соотношение (11-5) может быть переписано в виде:
, (11-6)
где 
- тензор диэлектрической проницаемости для кристаллов неактивных диэлектриков, и скаляр для аморфных диэлектриков.
Физический смысл индукции электрического поля состоит в том, что проекция 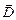на нормаль к поверхности источника внешнего электрического поля является плотностью электрического заряда на обкладках конденсатора. Диэлектрическая проницаемость 
изотропной среды (или среды с кубическим окружением) определяется соотношением:
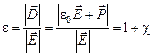. (11-8)
В этой формуле величина 
носит название диэлектрической восприимчивости.
Если твердое тело находится в аморфном агрегатном состоянии или представляет собой кубический кристалл, и при этом обладает электронной компонентой упругой поляризацией, то справедливо соотношение Клаузиуса-Мосотти:
. (11-9)
В этом соотношении 
- концентрация атомов или ионов 
- того сорта, имеющих 
коэффициент поляризуемости. В формуле (11-9) суммирование идет по всем сортам атомов или ионов в твердом теле.
При ориентационной поляризации в твердом теле (в отсутствие внешнего электрического поля), имеются дипольные моменты, причем величина модуля дипольного момента не зависит от величины локального электрического поля. В случае ориентационной поляризации твердого тела влияние электрического поля проявляется только в ориентации дипольных моментов и появлении зависящего от этого поля вектора поляризации. При снятии внешнего электрического поля тепловое движение приводит к хаотической ориентации дипольных моментов молекул - частиц твердого тела. Если не учитывать квантовых особенностей такого вида поляризации, состоящих в том, что углы разориентации дипольных моментов относительно выбранного направления в кристалле являются набором дискретных значений, то можно считать, что угол разориентации дипольного момента относительно выбранного направления может обладать непрерывным набором значений от 0 до 180 градусов. При этом среднее значение косинуса угла разориентации одного сорта дипольного момента подчиняется формуле Ланжевена:
|
|
|
, (11-10)
где 
. (11-11)
Если в твердом теле есть только один сорт частиц обладающих таким видом поляризации, то модуль вектора поляризации определяется выражением:
. (11-12)
Это соотношение при высоких температурах (т.е. при выполнении следующего неравенства):
):
приводит к выполнению закона Кюри (определенной зависимости диэлектрической восприимчивости от температуры):
. (11-13)
В некубических кристаллах связь между индукцией и напряженностью макроскопического электрического поля носит тензорный характер, и тогда для компоненты тензора диэлектрической проницаемости справедливо выражение:
. (11-14)
В случае активных диэлектриков – пьезоэлектриков, соотношение (11-5) в проекции на одну из координатных осей приобретает вид:
. (11-15)
В выражении (11-15) величина 
- является компонентой тензора пьезоэлектрического модуля, 
- компонента тензора механических напряжений, суммирование в третьем слагаемом проводится так, что индексы 
и 
пробегают целочисленные значения от единицы до трех. К пьезоэлектрикам относятся кристаллы, у которых элементарная ячейка не имеет центра симметрии. Для активных диэлектриков – пироэлектриков, электрическая индукция вдоль одной из пироэлектрических осей имеет вид:
. (11-16)
В это выражение, по сравнению с формулой (11-15), добавлены слагаемые пропорциональные пироэлектрическим модулям (
, 
) и, соответственно, первой и второй степеням изменения температуры (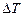
).
Для активных диэлектриков - сегнетоэлектриков в выражение
(11-16) добавляется компонента спонтанной поляризации 
:
, (11-17)
которая представляет собой проекцию вектора спонтанной поляризации на 
-ую ось.
Из всех известных 32 классов точечной симметрии кристаллов 20 классов обладают пьезоэлектрическими свойствами, а из них 10 классов обладают пироэлектрическими свойствами, а из последних - 4 класса обладают сегнетоэлектрическим свойствами.
|
|
|
