 |
Рекомбинация носителей заряда
|
|
|
|
Если имеет место возбуждение твердого тела с помощью внешнего воздействия, возникают неравновесные носители заряда. Причем концентрация свободных носителей заряда в полуметаллах, полупроводниках и диэлектриках при возбуждении (переводе в неравновесное состояние) может возрастать, в отличие от металлов, где концентрация носителей заряда постоянна. Генерацию носителей заряда описывают темпом генерации дырок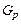 
и темпом генерации электронов 
. Одновременно с генерацией носителей заряда имеет место рекомбинация носителей заряда, ведущая к снижению концентрации неравновесных носителей заряда. Концентрацию неравновесных носителей заряда можно записать в виде суммы концентрации равновесных носителей заряда и концентрации избыточных носителей заряда, так для электронов:
, (5-1)
И для дырок:
. (5-2)
Возможна однополярная генерация, при которой генерируется один тип подвижных носителей заряда и неподвижные ионизированные атомы примеси. Кроме того, возможна биполярная генерация, при которой генерируются в равных концентрациях электроны и дырки.
Аналогично темпу генерации, темп рекомбинации может быть биполярным и однополярным. При биполярной рекомбинации одновременно исчезают электрон и дырка. Для описания поведения избыточных носителей заряда используют систему кинетических уравнений:
, (5-3)
. (5-4)
В этих уравнениях плотность тока 
- представляет собой плотность тока, связанную с движением электронов, а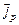 
, соответственно, - дырок. Если имеет место однородное возбуждение, то плотности обоих компонент тока равны нулю, и уравнения (26) и (27) упрощаются. Кроме того, если необходимо исследовать рекомбинацию носителей заряда после биполярного возбуждения, при отсутствии индивидуальных ловушек для электронов и таких же ловушек для дырок, то можно прийти к выводу, что во все время рекомбинации избыточная концентрация дырок равна избыточной концентрации электронов.
|
|
|
. (5-6)
Следовательно, можно упростить систему из уравнений (5-3) и (5-2) до одного уравнения:
, (5-7)
или полностью эквивалентного ему уравнения:
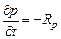. (5-8)
Темп рекомбинации отражает скорость приближения неравновесной концентрации носителей заряда к равновесной и одновременно степень отклонения от равновесного значения. При указанных выше ограничениях, и если предположить, что отсутствует поверхностная рекомбинация, то уравнение (29) может быть записано в виде:
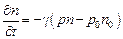. (5-8)
Кроме того, используя соотношения (24) и (25) приходят к уравнению:
. (5-9)
Это нелинейное уравнение можно решать в двух приближениях:
1) случай слабого возбуждения, при этом
,
2) случай сильного возбуждения, и тогда должно выполняться следующее неравенство:
.
Решение уравнения (31) для случая слабого возбуждения имеет вид:
, (5-10)
где введено обозначение:
. (5-11)
Величину 
называют временем жизни неосновных носителей заряда.
В случае сильного возбуждения решение уравнения (31) имеет вид:
. (5-12)
В формулах (5-10) и (5-12) величина 
есть концентрация избыточных носителей заряда в момент выключения возбуждения.
Диффузия носителей заряда
При наличии неоднородности концентрации носителей заряда, связанной с неоднородным легированием или неоднородным возбуждением полупроводника имеет место диффузия носителей заряда. Движущей силой диффузии является разность концентраций носителей заряда. В связи с этим появляются диффузионные токи. В металлах диффузионный ток реализовать невозможно, т.к. в этих твердых телах практически нельзя изменить концентрацию свободных носителей заряда. В полупроводниках при наличии нескольких видов носителей заряда диффузионная плотность тока может быть выражена следующим образом:
|
|
|
. (6-1)
Если же имеется градиент только одного сорта носителей заряда, например дырок и изменение концентрации дырок идет только в одном направлении (направлении оси Х), то выражение (6-1) записывается в виде:
, (6-2)
где 
- модуль заряда электрона, 
- коэффициент диффузии дырок.
Для невырожденных полупроводников коэффициент диффузии может быть найден в соответствии с соотношением Эйнштейна (так для диффузии дырок в электронном полупроводнике):
. (6-3)
Здесь 
- подвижность дырок. При диффузии носителей заряда имеет место рекомбинация избыточных неосновных носителей заряда. Если диффузия идет при отсутствии внешнего электрического поля, то концентрация избыточных неосновных носителей заряда изменяется по закону:
. (6-4)
Здесь - концентрация избыточных неосновных носителей заряда электронов в p-области на границе p-области или области возбуждения, 
- диффузионная длина. Этот параметр материала для невырожденного полупроводника зависит от коэффициента диффузии и времени жизни избыточных неосновных носителей заряда:
. (6-5)
В этом выражении 
- коэффициент диффузии электронов, 
- время жизни электронов в образце p-типа с конкретной концентрацией основных носителей заряда и концентрацией рекомбинационных центров. Длину диффузии можно определить как расстояние на которое в среднем могут смещаться избыточные неосновные носители заряда за время, равное времени жизни.
Если концентрация носителей заряда постоянна, но коэффициент диффузии, например, электронов зависит от температуры 
, то при постоянном значении концентрации носителей заряда может появляться плотность ток термодиффузии. Так для одномерного случая в полупроводнике n-типа ток термодиффузии электронов описывается формулой: 
. (6-6)
Используя явление термодиффузии можно определять тип основных носителей заряда в полупроводнике.
|
|
|
