 |
Предпосылки МНК (см. вопр. 4)
|
|
|
|
Эмпирическое уравнение регрессии:
Отклонение еi эмпирического значения yi от рассчитанного с пом. МНК значения yi:
По МНК: 
Условие минимума функции - равенство нулю всех ее частных производных по bj. Частные производные квадратичной функции являются линейными функциями.
Система нормальных уравнений МНК:
Матричная форма:
Y − вектор-столбец размерности n наблюдений зависимой переменной Y;
Х − матрица размерности n × (m + 1), в которой i-я строка (i = 1, 2, …, n) представляет наблюдение вектора значений независимых переменных X1, X2, …, Xm; единица соответствует переменной при свободном члене b0;
B − вектор-столбец размерности (m+ 1) параметров уравнения регрессии;
e − вектор-столбец размерности n отклонений выборочных (реальных) значений yi зависимой переменной Y от значений yi
e = Y − XB
Свойства МНК-оценок множественной линейной регрессии. Теорема Гаусса- Маркова.
Условия Гаусса-Маркова (свойства МНК-оценок)
1. 
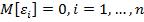– условие, гарантирующее несмещённость оценок МНК.
2. 
– условие гомоскедастичности.
3. 
– условие отсутствия автокорреляции предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях.
4. 
для всех 
- условие независимости случайного возмущения и объясняющей переменной. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.
Теорема Гаусса-Маркова: если выполнены условия Гаусса-Маркова, тогда оценки 
, полученные с помощью метода наименьших квадратов, являются линейными, несмещёнными, эффективными и состоятельными оценками.
|
|
|
1. Линейность оценок – оценки параметров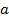 
и 
представляют собой линейные комбинации наблюдаемых значений объясняемой переменной 
.
2. Несмещённость оценок:
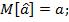
3. Состоятельность оценок:
Чем больше наблюдений, тем ближе подсчитанные а и б к реальным.
4. Эффективность – означает, что оценка имеет минимальную дисперсию в заданном классе оценок:
Другое
Свойство эффективности оценок неизвестных параметров модели регрессии, полученных методом наименьших квадратов, доказывается с помощью теоремы Гаусса-Маркова.
Сделаем следующие предположения о модели парной регрессии:
1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:;
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
Это условие выполняется в том случае, если исходные данные не являются временными рядами;
5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2:
Если выдвинутые предположения справедливы, то оценки неизвестных параметров модели парной регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров и.
Если выдвинутые предположения справедливы для модели множественной регрессии, то оценки неизвестных параметров данной модели регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров.
|
|
|
Для обозначения дисперсий МНК-оценок неизвестных параметров модели регрессии используется матрица ковариаций.
Матрицей ковариаций МНК-оценок параметров линейной модели парной регрессии называется выражение вида:
где
– дисперсия МНК-оценки параметра модели регрессии;
– дисперсия МНК-оценки параметра модели регрессии.
Матрицей ковариаций МНК-оценок параметров линейной модели множественной регрессии называется выражение вида:
где G2() – это дисперсия случайной ошибки модели регрессии.
Для линейной модели парной регрессии дисперсии оценок неизвестных параметров определяются по формулам:
1)
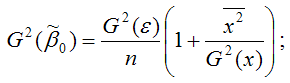
2) дисперсия МНК-оценки коэффициента модели регрессии:
где G2() – дисперсия случайной ошибки уравнения регрессии;
G2(x) – дисперсия независимой переменой модели регрессии х;
n – объём выборочной совокупности.
В связи с тем, что на практике значение дисперсии случайной ошибки модели регрессии G2() неизвестно, для вычисления матрицы ковариаций МНК-оценок применяют оценку дисперсии случайной ошибки модели регрессии S2().
Для линейной модели парной регрессии оценка дисперсии случайной ошибки определяется по формуле:
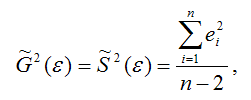
где
– это остатки регрессионной модели, которые рассчитываются как
Тогда оценка дисперсии МНК-оценки коэффициента линейной модели парной регрессии будет определяться по формуле:
Оценка дисперсии МНК-оценки коэффициента линейной модели парной регрессии будет определяться по формуле:
Для модели множественной регрессии общую формулу расчёта матрицы ковариаций МНК-оценок коэффициентов на основе оценки дисперсии случайной ошибки модели регрессии можно записать следующим образом:
|
|
|
