 |
Спецификация эконометрической модели: способы и диагностика отбора экзогенных переменных. Тесты Рамсея и Амемья.
|
|
|
|
Спецификация модели множественной линейной регрессии включает проверку:
1. правильного выбора экзогенных переменных.
2. корректного выбора формы зависимости мду эндо- и экзогенной переменными.
Для решения 1 задачи различают пропущенные и избыточные экзогенные переменные
Пропущенные переменные – существенные факторы, которые не были включены в эконометрическую модель по ошибке. Опасность наличия пропущенных переменных заключается в смещении оценок параметров при включенных переменных. Признак, по которому определяют пропущенную переменную: Знак “+” у произведения оценки параметра при подозреваемой пропущенной переменной и коэффициента корреляции этой переменной с другими переменными, включенными в модель.
Истинная модель:
Выбранная модель с пропуском переменной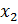 
:
, где 
Тогда, применяя МНК для оценки усеченной модели получаем формулу смещения оценки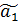 
^
Экзогенную переменную относят к избыточным, если она по ошибке включена в эконометрическую модель. Включение избыточной переменной оказывает влияние на уменьшение точности (увеличение дисперсии) оценок параметров модели, что, в свою очередь, вызывает уменьшение t-статистик и коэффициента детерминации.
Если 
– избыточная, то коэффициент корреляции 
, тогда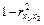 
будет уменьшаться, а в соответствии с формулой 
будет возрастать.
Замещающие переменные – обычно бывает полезно вместо пропущенной переменной, которую трудно измерить, использовать некоторый её заменитель.
4 основных качественных правила спецификации экономической модели:
1. Опираясь на эконометрическую теорию, следует ответить на вопрос: «Является ли переменная существенной в модели зависимости с эндогенной переменной?».
|
|
|
2. Осуществить проверку значимого отличия от нуля t -статистик.
3. Осуществить проверку, насколько значимо изменяется коэффициент детерминации при добавлении некоторой переменной в модель.
4. Существенно ли изменяются оценки других переменных после добавления новой переменной в модель.
Кроме отмеченных правил спецификации модели, наиболее из-вестны два следующих количественных критерия спецификации:
Критерий Рамсея (Ramsey):
RESET-тест Рамсея - это обобщенный тест на наличие следующих ошибок спецификации модели линейной регрессии:
- наличие пропущенных переменных. Регрессия содержит не все объясняющие переменные;
- неверная функциональная форма. Некоторые или все переменные должны быть преобразованы с помощью логарифмической, степенной, обратной или какой-либо другой функции;
- корреляция между фактором Х и случайной составляющей модели, которая может быть вызвана ошибками измерения факторов, рассмотрением систем уравнений или другими причинами.
Тест Рамсея позволяет проверить, стоит ли начинать поиск дополнительной переменной для включения в уравнение
1. Оценивается уравнение регрессии
2. Вычисляются степени оценок зависимой переменной
3. Оценивается уравнение регрессии с этими степенями
4. Проводится оценка улучшения по F-критерию
Ошибки такого рода приводят к смещению среднего остатков регрессионной модели.
1. Оценивают зависимость в соответствии с выбранной моделью по МНК:
2. Анализируют вид функциональной зависимости остатков 
и её номинальное приближение включают в модель.
3. Например, с учетом 2) вычисляют величины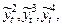 
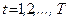, конструируют новую модель:
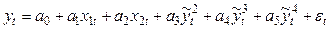
и применяют для ее оценивания по МНК.
4) Сравнивают качество модели по отношению к модели с помощью F -критерия:
Если 
где M – число дополнительных переменных, включенных в модель (M =3), k – число экзогенных переменных в 
то модель плохо специфицирована.
|
|
|
Недостаток: он указывает только на наличие ошибочной спец-ции модели, но не выявляет, сколько и какого рода переменную нужно добавить в модель.
Критерий Амемья (Amemiya):
Решающей функцией F-критерия служит:
Модель, для которой значение AF меньше, является лучше специфицированной.
Этот критерий минимизирует число экзогенных переменных.
|
|
|
