Нестационарная модель АРИСС. Оценка параметров модели.

Модель, учитывающая последовательные разности, носит название авторегрессии и интегрированного скользящего среднего АРИСС (p, d, q). Например, АРИСС (2, 1, 1) указывает на включение в уравнение двух авторегрессионных слагаемых (из конечных разностей первого порядка) и одного слагаемого модели скользящего среднего:

АРИСС (2, 1, 1):

В условиях применения АРИСС-модели возникают три основные задачи:

· оценка структуры модели, то есть спецификация параметров p,

d и q;

· оценка коэффициентов модели;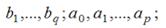

· прогнозирование переменной Y_T+k модели.

Перейдем к решению этих задач:

1. Процедура спецификации модели обычно начинается с решения задачи оценивания порядка включаемых в модель конечных разностей d.

Шаг 1. Производят изучение выборки данных, если Y проявляет тенденцию к росту, то вычисляют конечные разности 1-го порядка 🔺Y_t.

Шаг 2. Проверяют парный коэффициент корреляции p₁ между зависимой переменной Y_t и лаговой переменной Y_t-1. При корректном выборе параметра d индикатор 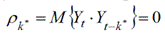, тогда в качестве оценки d принимают k *. Изобразим алгоритм остановки процесса преобразования исходной модели к стационарной с помощью графика p_k, который носит название кореллограммы:

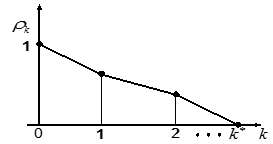
Рис.25

2. Нахождение оценок параметров авторегрессии p и скользящего среднего осуществляют в три этапа.

Этап 1. Выбирают начальные значения p и q₀, по возможности наименьшие p = p₀, q = q₀.

Этап 2. Оценивают АРИСС (p₀,d,q₀) и находят остатки e_t, с помощью которых рассчитывают частные коэффициенты автокорреляции:

.

Если p(k)=0, то сохраняют p = p₀ и q = q₀, в противном случае увеличивают начальные значения ρ и q на единицу и повторяют этап 2 для модели АРИСС (p₀,d,q₀) до тех пор, пока коэффициенты частной корреляции не обратятся в нуль.

Приведем таблицу выбора моделей низких порядков АРИСС на базе определенных значений коэффициентов корреляции.

Модель	p	p(k)
Нестационарная	Отличен от нуля	Отличен от нуля
АРИСС(0, 0, 0)	Все равны нулю	Все равны нулю
АРИСС(1, 0, 0)	Стремятся к нулю	Обращаются в 0 после 1-ого лага
АРИСС(2, 0, 0)	Стремятся к нулю	Обращаются в 0 после 2-ого лага
АРИСС(0, 0, 1)	Обращаются в 0 после 1-ого лага	Стремятся к 0
АРИСС(0, 0, 2)	Обращаются в 0 после 2-ого лага	Стремятся к 0
АРИСС(1, 0, 1)	Обращаются в 0 после 1-ого лага	Обращаются в 0 после 1-ого лага

Этап 3. Закончив процесс оценивания структуры модели АРИСС, переходят к оцениванию ее коэффициентов. Следует заметить, что лишь при q=0 целесообразно применять классический МНК, а в противном случае требуется использовать операторы декорреляции или взвешенные модификации МНК.

Для решения задачи нахождения прогноза используют модель

с наблюдаемыми остатками e_t:

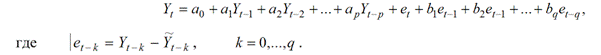
Процесс построения прогнозируемых значений происходит последовательно, начиная с оценки прогноза на один период, используя который, получают прогноз на 2 периода в будущее и так далее. Проиллюстрируем этот процесс для модели АРИСС (2, 0, 1):

,.

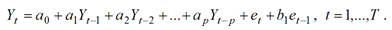Для нахождения прогноза в момент времени Т+ 1 оценивают коэффициенты и после подстановки получают:

,

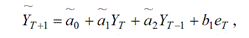где остаток, полученный в момент Т +1, равен нулю. Далее, для получения прогноза в момент Т +2, имеют

.

Заметим, что процесс скользящего среднего с момента Т +2 уже не участвует в прогнозировании.

Модель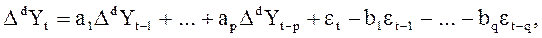

описывает нестационарные временные ряды 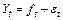с трендовой аддитивной составляющей 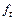, имеющие вид алгебраического полинома степени k – 1 с коэффициентами любого типа (случайного / детерминированного).

Кривые роста описывают закономерности развития явлений во времени посредством аналитического выравнивания рядов динамики. Кривые роста, описывающие 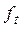, имеют следующий вид (табл. 1):

Кривая роста	Вид тренда	Подбор	Характер изменения во времени
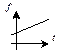
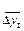
Линейная			Примерно одинаковые
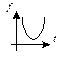
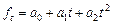
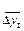
Парабола 2го порядка			Линейно изменяются
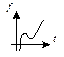
Кубическая парабола			Линейно изменяются
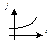
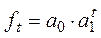
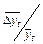
Показательная			Примерно одинаковые
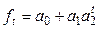
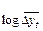
Модифицированная показательная			Линейно изменяются
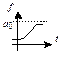
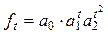
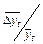
Логарифмическая парабола			Линейно изменяются
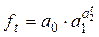
Кривая Гомперца			Линейно изменяются
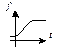
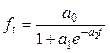
Логистическая кривая			Линейно изменяются

⇐ Предыдущая123456789

Поделиться:

Воспользуйтесь поиском по сайту: