Модели с распределенными лагами: структура лагов по Койку: Частные случаи (модель с неполной корректировкой и адаптивных ожиданий)

Примеры макроэкономических моделей, в которых важен временной лаг:

● функция потребления;

● создание денег в банковской системе;

● связь между денежной массой и уровнем цен;

● лаг между расходами на НИОКР и производительностью;

● "кривая джей" (J-curve) связи между валютным курсом и торговым балансом;

● модель акселератора инвестиций.

Причин наличия лагов в экономике достаточно много, и среди них можно выделить следующие:

● Психологические причины – обычно выражаются через инерцию в поведении людей. Например, люди тратят свой доход постепенно, а не мгновенно. Привычка к определенному образу жизни приводит к тому, что люди приобретают те же блага в течение некоторого времени даже после падания реального дохода.

● Технологические причины – например, изобретение персональных компьютеров не привело к мгновенному вытеснению ими больших ЭВМ в силу необходимости замены соответствующего программного обеспечения, которое потребовало продолжительного времени.

● Институциональные причины – например, контракты между фирмами, трудовые договоры требуют определенного постоянства в течение времени контракта.

● Механизм формирования экономических показателей – например, инфляция во многом является инерционным процессом, денежный мультипликатор также проявляет себя на определенном временном интервале.

Основную сложность для эмпирической оценки модели с распределённым лагом представляет наличие мультиколлинеарности, т.к. в экономических данных соседние значения одного и того же ряда данных обычно высоко коррелированы друг с другом. Кроме того, не всегда возможно априори определить, сколько лаговых переменных стоит включать в модель. Существуют даже модели с бесконечным числом лаговых регрессов, коэффициенты при которых бесконечно уменьшаются (например, в геометрической прогрессии). Существует множество специальных технологий для работы с распределенными лагами: так, метод Тинбергена и Альта представляет собой "метод большого пальца" для определения оптимального числа лаговых переменных, не внося дополнительных предпосылок в модель. Модели Койка и Алмон, напротив, вводят предпосылки относительно лаговых коэффициентов, позволяющие упростить их оценку.

Подход Тинбергена и Альта

Подход Тинбергена и Альта позволяет нащупать баланс между точностью модели (числом включенных лаговых переменных) и качеством оценки (мультиколлинеарностью). Он предполагает последовательную оценку моделей:

Остановка процесса рекомендуется, когда какой-либо из коэффициентов при лаговых переменных меняет знак или становится статистически незначимым, что является следствием возникновения мультиколлинеарности. Кроме того, маловероятна, но возможна такая ситуация, когда просто не будет достаточно наблюдений для дальнейшего увеличения числа лаговых переменных.

Преобразование Койка

Преобразование Койка — приём, позволяющий оценить модель с распределёнными лагами путём простого предположения о том, что коэффициенты при лаговых переменных убывают в геометрической прогрессии с увеличением лага:

В этой модели несложно найти средний лаг , а также медианный лаг .

Вычтя из данного уравнения уравнение для ,умноженное на , получаем простую модель:

Эта модель легко может быть оценена обычным методом наименьших квадратов без потери степеней свободы. Здесь, однако, существует автокорреляция случайного члена 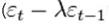с , и, что хуже, случайный член коррелирует с объясняющей переменной . Поэтому для оценки модели рекомендуется использовать метод инструментальных переменных или оценивать исходную модель с помощью нелинейного метода наименьших квадратов.

Преобразование Койка иллюстрирует взаимосвязь моделей с распределённым лагом и авторегрессионных моделей. Модели Койка соответствуют два широко применяемых теоретических подхода к распределённым лагам: модель адаптивных ожиданий и модель частичной подстройки.