 |
Глава 1. Делимость в кольце чисел Гаусса.
|
|
|
|
Вятский государственный гуманитарный университет
Математический факультет
Кафедра математического анализа и методики
преподавания математики
Выпускная квалификационная работа
На тему: Кольцо целых чисел Гаусса.
Выполнил:
студент V курса
математического факультета
Гнусов В.В.
___________________________
Научный руководитель:
старший преподаватель кафедры
алгебры и геометрии
Семенов А.Н..
___________________________
Рецензент:
кандидат физ.-мат. наук, доцент
кафедры алгебры и геометрии
Ковязина Е.М.
___________________________
Допущена к защите в ГАК
Зав. кафедрой________________ Вечтомов Е.М.
«»________________
Декан факультета___________________ Варанкина В.И.
«»________________
Киров 2005
Содержание.
Введение. 2
ГЛАВА 1. ДЕЛИМОСТЬ В КОЛЬЦЕ ЧИСЕЛ ГАУССА. 3
1.1 ОБРАТИМЫЕ И СОЮЗНЫЕ ЭЛЕМЕНТЫ. 4
1.2 ДЕЛЕНИЕ С ОСТАТКОМ. 5
1.3 НОД. АЛГОРИТМ ЕВКЛИДА. 6
1.4 ОСНОВНАЯ ТЕОРЕМА АРИФМЕТИКИ. 9
ГЛАВА 2. ПРОСТЫЕ ЧИСЛА ГАУССА. 12
ГЛАВА 3. ПРИМЕНЕНИЕ ЧИСЕЛ ГАУССА. 17
Заключение. 23
Введение.
Кольцо целых комплексных чисел 
было открыто Карлом Гауссом и названо в его честь гауссовым.
К. Гаусс пришел к мысли о возможности и необходимости расширения понятия целого числа в связи с поиском алгоритмов решения сравнений второй степени. Он перенес понятие целого числа на числа вида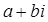 
, где 
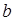— произвольные целые числа, а 
— является корнем уравнения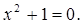 
На данном множестве К. Гаусс впервые построил теорию делимости, аналогичную теории делимости целых чисел. Он обосновал справедливость основных свойств делимости; показал, что в кольце комплексных чисел существует только четыре обратимых элемента: 
; доказал справедливость теоремы о делении с остатком, теоремы о единственности разложения на простые множители; показал какие простые натуральные числа останутся простыми и в кольце ; выяснил природу простых целых комплексных чисел.
|
|
|
Развитая К. Гауссом теория, описанная в его труде «Арифметические исследования», явилась фундаментальным открытием для теории чисел и алгебры.
В выпускной работе были поставлены следующие цели:
1. Развить теорию делимости в кольце чисел Гаусса.
2. Выяснить природу простых гауссовых чисел.
3. Показать применение гауссовых чисел при решении обычных диофантовых задач.
ГЛАВА 1. ДЕЛИМОСТЬ В КОЛЬЦЕ ЧИСЕЛ ГАУССА.
Рассмотрим множество комплексных чисел. По аналогии с множеством действительных чисел в нем можно выделить некоторое подмножество целых чисел. Множество чисел вида 
, где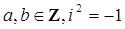 
назовем целыми комплексными числами или гауссовыми числами. Нетрудно проверить, что для этого множества выполняются аксиомы кольца. Таким образом, это множество комплексных чисел является кольцом и называется кольцом целых чисел Гаусса. Обозначим его как 
, так как оно является расширением кольца 
элементом: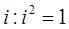 
.
Поскольку кольцо гауссовых чисел является подмножеством комплексных чисел, то для него справедливы некоторые определения и свойства комплексных чисел. Так, например, каждому гауссовому числу соответствует вектор с началом в точке 
и с концом в 
. Следовательно, модуль гауссова числа есть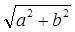 
. Заметим, что в рассматриваемом множестве, подмодульное выражение всегда есть число неотрицательное целое. Поэтому в некоторых случаях удобнее пользоваться нормой, то есть квадратом модуля. Таким образом 
. Можно выделить следующие свойства нормы. Для любых гауссовых чисел 
справедливо:
|
|
|
(1)
(2)
(3)
(4)
(5)
Здесь и далее 
— множество натуральных чисел, то есть целых положительных чисел.
Справедливость данных свойств тривиальным образом проверяется с помощью модуля. Попутно заметим, что (2), (3), (5) справедливы и для любых комплексных чисел.
Кольцо гауссовых чисел — это коммутативное кольцо без делителей 0, так как оно является подкольцом поля комплексных чисел. Отсюда следует мультипликативная сократимость кольца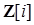 
, то есть
(6)
|
|
|
