 |
Лемма 3. О представлении НОД.
|
|
|
|
Если НОД(
, 
)= 
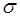, то существуют такие целые гауссовы числа 
и 
, что 
.
Доказательство.
Рассмотрим снизу вверх цепочку равенств, полученную в алгоритме Евклида. Последовательно подставляя вместо остатков их выражения через предыдущие остатки, мы выразим 
через и .
Ч.Т.Д.
Гауссово число называется простым, если его нельзя представить в виде произведения двух необратимых сомножителей. Следующее утверждение очевидно.
Утверждение 4.
При умножении простого гауссова числа на обратимое снова получается простое гауссово число.
Утверждение 5.
Если у гауссова числа взять необратимый делитель с наименьшей нормой, то он будет простым гауссовым.
Доказательство.
Пусть такой делитель 
является составным числом. Тогда 
, где 
и 
необратимые гауссовы числа. Перейдем к нормам, и согласно (3) получим, что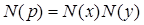 
. Так как эти нормы натуральны, то имеем, что 
, а в силу (12), 
является необратимым делителем данного числа Гаусса, что противоречит выбору .
Ч.Т.Д.
Утверждение 6.
Если не делится на простое гауссово число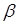 
, то НОД(
, 
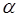)=1.
Доказательство.
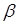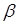Действительно, простое число делится только на числа союзные с 1 или с . А так как не делится на , то на союзные с 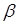тоже не делится. Значит, их общими делителями будут только обратимые числа.
Ч.Т.Д.
Лемма 7. Лемма Евклида.
Если произведение гауссовых чисел делится на простое гауссово число 
, то хотя бы один из множителей делится на 
.
Доказательство.
Для доказательства достаточно рассмотреть случай, когда произведение содержит только два множителя. То есть покажем, что если 
делится на 
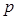, то либо делится на 
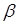, либо делится на .
Пусть не делится на , тогда НОД(
, )=1. Следовательно, существуют такие гауссовы числа и 
, что 
. Умножим обе части равенства на , получим, что 
, отсюда следует, что 
, как сумма чисел делящихся на .
|
|
|
Ч.Т.Д.
ОСНОВНАЯ ТЕОРЕМА АРИФМЕТИКИ.
Любое ненулевое гауссово число можно представить в виде произведения простых гауссовых чисел, причем это представление единственно с точностью до союзности и порядка сомножителей.
Замечание 1.
Обратимое число имеет в своем разложении нуль простых множителей, то есть представляется самим собой.
Замечание 2.
Более точно единственность формулируется следующим образом. Если имеются два разложения на простые гауссовы множители, то есть 
, то 
и можно так перенумеровать числа 
, что 
будет союзно с 
, при всех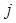 
от 1 до 
включительно.
Доказательство.
Доказательство проведем индукцией по норме.
База. Для числа с единичной нормой утверждение очевидно.
Пусть сейчас — ненулевое необратимое гауссово число, и для всех чисел Гаусса с нормой меньшей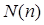 
утверждение доказано.
Покажем возможность разложения на простые множители. Для этого обозначим через 
необратимый делитель , имеющий наименьшую норму. Этот делитель должен быть простым числом по утверждению 5. Тогда 
. Таким образом, мы имеем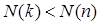 
и по индуктивному предположению 
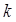представимо в виде произведения простых чисел. Значит, раскладывается в произведение этих простых и .
Покажем единственность разложения на простые множители. Для этого возьмем два произвольных таких разложения:
.
По лемме Евклида в произведении 
один из множителей должен делиться на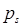 
. Можно считать, что 
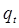делится на 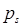, иначе перенумеруем. Так как они простые, то 
, где 
обратимо. Сокращая обе части нашего равенства на 
, получим разложение на простые множители числа 
, по норме меньшего, чем 
.
.
По индуктивному предположению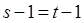 
и можно перенумеровать числа 
так, что 
будет союзно с 
, 
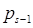с 
, …, 
с 
. Тогда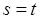 
и при этой нумерации союзно с при всех 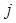от 1 до 
включительно. Значит, разложение на простые множители единственно.
|
|
|
Ч.Т.Д.
Пример однопорожденного кольца над 
без ОТА.
Рассмотрим 
. Элементами этого кольца являются числа вида 
, где 
и 
произвольные целые числа. Покажем, что в нем не выполняется основная теорема арифметики. Определим в этом кольце норму числа 
следующим образом: 
. Это действительно является нормой, так как нетрудно проверить, что 
. Пусть 
и 
. Тогда
.
Заметим, что 
.
Покажем, что в рассматриваемом кольце числа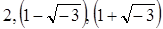 
являются простыми. Действительно, пусть 
— одно из них и 
. Тогда имеем: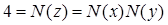 
Так как в этом кольце нет чисел с нормой 2, то 
или 
. Обратимыми элементами будут числа с единичной нормой и только они. Значит, в произвольном разложении на множители найдется обратимый множитель, следовательно, просто.
|
|
|
