 |
Глава 3. Применение чисел Гаусса.
|
|
|
|
Утверждение.
Произведение чисел представимых в виде суммы двух квадратов также представимо в виде суммы двух квадратов.
Доказательство.
Докажем этот факт двумя способами, с помощью чисел Гаусса, и не используя гауссовы числа.
1. Пусть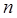 
, 
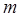— натуральные числа представимые в виде суммы двух квадратов. Тогда 
, и 
. Рассмотрим произведение 
, то есть представили в виде произведения двух сопряженных гауссовых чисел, которое представляется в виде суммы двух квадратов натуральных чисел.
2. Пусть 
, 
. Тогда
.
Ч.Т.Д.
Утверждение.
Если 
, где 
— простое натуральное вида 
, то 
и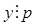 
.
Доказательство.
Из условия следует, что 
и при этом 
— простое гауссово. Тогда по лемме Евклида на делится один из множителей. Пусть 
, тогда по лемме 10 имеем, что 
и 
.
Ч.Т.Д.
Опишем общий вид натуральных чисел представимых в виде суммы двух квадратов.
Рождественская теорема Ферма или теорема Ферма — Эйлера.
Ненулевое натуральное число представимо в виде суммы двух квадратов тогда, и только тогда, когда в каноническом разложении все простые множители вида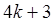 
входят в четных степенях.
Доказательство.
Заметим, что 2 и все простые числа вида 
представимы в виде суммы двух квадратов. Пусть в каноническом разложении числа есть простые множители вида 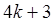, входящие в нечетной степени. Занесем в скобки все множители представимые в виде суммы двух квадратов, тогда останутся множители вида 
, причем все в первой степени. Покажем, что произведение таких множителей не представимо в виде суммы двух квадратов. Действительно, если допустить, что 
, то имеем, что 
должен делить один из множителей 
или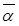 
, но если 
делит одно из этих гауссовых чисел, то оно обязано и делить другое, как сопряженное к нему. То есть 
и 
, но тогда должно быть во второй степени, а оно в первой. Следовательно, произведение любого числа простых множителей вида 
первой степени не представимо в виде суммы двух квадратов. Значит наше предположение не верно и все простые множители вида в каноническом разложении числа входят в четных степенях.
|
|
|
Ч.Т.Д.
Задача 1.
Посмотрим применение данной теории на примере решения диафантова уравнения.
Решить в целых числах 
.
Заметим, что правая часть представима в виде произведения сопряженных гауссовых чисел.
То есть 
. Пусть 
делится на некоторое простое гауссово число , и на него делится и сопряженное, то есть 
. Если рассмотреть разность этих гауссовых чисел, которая должна делиться на , то получим, что должно делить 4. Но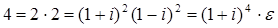 
, то есть союзно с 
.
Все простые множители в разложении числа 
входят в степени кратной трем, а множители вида 
, в степени кратной шести, так как простое гауссово число 
получается из разложения на простые гауссовы 2, но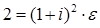 
, поэтому 
. Сколько раз 
встречается в разложении на простые множители числа 
, столько же раз и встречается в разложении на простые множители числа 
. В силу того, что 
делится на 
тогда и только тогда, когда 
делится на 
. Но союзно с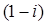 
. То есть они распределятся поровну, значит, будут входить в разложения этих чисел в степенях кратной трем. Все остальные простые множители, входящие в разложение числа 
, будут входить только либо в разложение числа 
, либо числа 
. Значит, в разложении на простые гауссовы множители числа все множители будут входить в степени кратной трем. Следовательно число есть куб. Таким образом имеем, что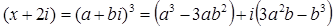 
. Отсюда получаем, что 
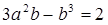, то есть 
должно быть делителем 2. Значит 
, или 
. Откуда получаем четыре удовлетворяющие нам варианта.
1. 
, 
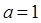. Откуда находим, что 
, 
.
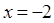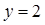2. 
, . Отсюда 
, 
.
3. , 
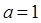. Отсюда 
, 
.
|
|
|
4. 
, 
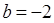. Отсюда 
, .
Ответ: 
, 
, 
, 
.
Задача 2.
Решить в целых числах 
.
Представим левую часть как произведению двух гауссовых чисел, то есть 
. Разложим каждое из чисел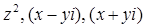 
на простые гауссовы множители. Среди простых будут такие, которые есть в разложении 
и 
. Сгруппируем все такие множители и обозначим полученное произведение 
. Тогда в разложении 
останутся только те множители, которых нет в разложении . Все простые гауссовы множители, входящие в разложение 
, входят в четной степени. Те которые не вошли в будут присутствовать либо только в 
, либо в 
. Таким образом, число 
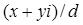является квадратом. То есть 
. Приравнивая действительные и мнимые части, получим, что 
, 
, 
.
Ответ: 
, , .
Задача 3.
Количество представлений натурального числа в виде суммы двух квадратов.
Задача равносильна задаче о представлении данного натурального числа в виде нормы некоторого числа Гаусса. Пусть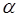 
— число Гаусса, норма которого равна 
. Разложим 
на простые натуральные множители.
, где 
— простые числа вида 
, а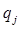 
— простые числа вида 
. Тогда, чтобы было представимо в виде суммы двух квадратов, необходимо, чтобы все 
были четными. Разложим на простые гауссовы множители число 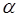, тогда
,
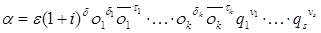где 
— простые гауссовы числа, на которые раскладываются 
.
Сравнение нормы 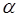с числом приводит к следующим соотношениям, необходимым и достаточным для того, чтобы 
:
.
Число представлений подсчитывается из общего числа возможностей для выбора показателей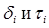 
. Для показателей 
имеется 
возможность, так как число 
можно разбить на два неотрицательных слагаемых способом:
Для пары показателей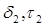 
имеется 
возможность и так далее. Комбинируя всевозможными способами допустимые значения для показателей 
мы получим всего 
различных значений для произведения простых гауссовых чисел, с нормой вида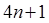 
или 2. Показатели 
выбираются однозначно. Наконец, обратимому 
можно придавать четыре значения: 
.Таким образом, для числа 
имеется всего 
возможностей, и следовательно, число в виде нормы гауссова числа 
, то есть в виде 
может быть представлено 
способами.
При этом подсчете различными считаются все решения уравнения 
. Однако некоторые решения можно рассматривать, как определяющие одно и то же представление в виде суммы двух квадратов. Так, если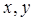 
— решения уравнения 
, то можно указать еще семь решений, определяющих то же самое представление числа в виде суммы двух квадратов: 
.
|
|
|
Очевидно, что из восьми решений, соответствующих одному представлению, может остаться только четыре различных в том и только в том случае, если 
или 
, или 
. Подобные представления возможны, если полный квадрат или удвоенный полный квадрат, и при том такое представление может быть только одно: 
.
Таким образом, имеем следующие формулы:
, если не все 
четные и
, если все четные.
Заключение.
В данной работе была изучена теория делимости в кольце целых чисел Гаусса, а также природа простых гауссовых чисел. Эти вопросы изложены в первых двух главах.
В третей главе рассмотрены применения чисел Гаусса к решению известных классических задач, таких как:
· Вопрос о возможности представления натурального числа в виде суммы двух квадратов;
· Задача нахождения количества представлений натурального числа в виде суммы двух квадратов;
· Нахождение общих решений неопределенного уравнения Пифагора;
а также к решению диафантова уравнения.
Также отмечу, что работа была выполнена без использования дополнительной литературы.
|
|
|
