 |
Глава 2. Простые числа Гаусса.
|
|
|
|
Чтобы понять какие гауссовы числа являются простыми, рассмотрим ряд утверждений.
Теорема 8.
Каждое простое гауссово является делителем ровно одного простого натурального.
Доказательство.
Пусть 
— простое гауссово, тогда 
. По основной теореме арифметики натуральных чисел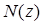 
раскладывается в произведение простых натуральных. А по лемме Евклида хотя бы один из них делится на .
Покажем сейчас, что простое Гауссово не может делить два различных простых натуральных. Действительно, пусть 
и 
различные простые натуральные, делящиеся на . Поскольку НОД(
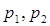)=1, то по теореме о представлении НОД в целых числах существуют 
и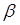 
— целые числа такие, что 
. Отсюда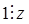 
, что противоречит простоте .
Ч.Т.Д.
Таким образом, раскладывая каждое простое натуральное на простые гауссовы, мы переберем все простые гауссовы, причем без повторений.
Следующая теорема показывает, что каждого простого натурального «получается» не более двух простых гауссовых.
Теорема 9.
Если простое натуральное разложено в произведение трех простых гауссовых, то хотя бы один из множителей обратим.
Доказательство.
Пусть 
— простое натуральное такое, что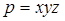 
. Перейдя к нормам, получим:
.
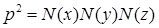Из этого равенства в натуральных числах следует, что хотя бы одна из норм равна 1. Следовательно, хотя бы одно из чисел 
— обратимо.
Ч.Т.Д.
Лемма 10.
Если гауссово число 
делится на простое натуральное 
, то 
и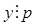 
.
Доказательство.
Пусть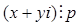 
, то есть 
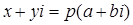. Тогда 
, 
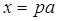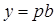, то есть , 
.
Ч.Т.Д.
Лемма 11.
Для простого натурального числа вида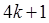 
, 
существует натуральное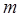 
такое, что 
.
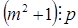Доказательство.
Теорема Вильсона гласит, что целое число 
является простым тогда и только тогда, когда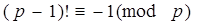 
. Но 
, отсюда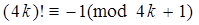 
. Раскроем и преобразуем факториал:
|
|
|
.
Отсюда получаем, что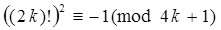 
, т.е. 
.
Таким образом, мы получили, что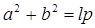 
, где = 
.
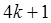Ч.Т.Д.
Сейчас мы готовы описать все простые гауссовы числа.
Теорема 12.
Все простые гауссовы можно разбить на три группы:
1). Простые натуральные вида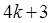 
, являются простыми гауссовыми;
2). Двойка союзна с квадратом простого гауссова числа 
;
3). Простые натуральные вида 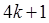, раскладываются в произведение двух простых сопряженных гауссовых.
Доказательство.
1). Предположим, что простое натуральное вида 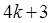не является простым гауссовым. Тогда 
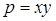, причем 
и 
. Перейдем к нормам: 
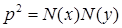. Учитывая указанные неравенства, получим 
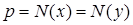, то есть — сумма квадратов двух целых чисел. Но сумма квадратов целых чисел не может давать остаток 3 при делении на 4.
2). Заметим, что
.
Число — простое гауссово, так как иначе двойка разложилась бы на три необратимых множителя, что противоречит теореме 9.
3). Пусть простое натуральное вида 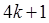, тогда по лемме 11 существует целое число 
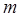такое, что 
. Пусть — простое гауссово. Так как 
, то по лемме Евклида на делится хотя бы один из множителей. Пусть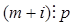 
, тогда существует гауссово число такое, что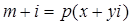 
. Приравнивая коэффициенты мнимых частей получим, что 
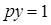. Следовательно, 
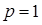, что противоречит нашему предположению о простоте . Значит — составное гауссово, представимое в виде произведения двух простых сопряженных гауссовых.
Ч.Т.Д.
Утверждение.
Гауссово число, сопряженное к простому, само является простым.
Доказательство.
Пусть 
простое число гаусса. Если предположить, что 
составное, то есть 
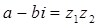. Тогда рассмотрим сопряженное: 
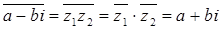, то есть представили в виде произведения двух необратимых сомножителей, чего не может быть.
Ч.Т.Д.
Утверждение.
Гауссово число, норма которого есть простое натуральное число, является простым гауссовым числом.
|
|
|
Доказательство.
Пусть составное число, тогда 
. Рассмотрим нормы.
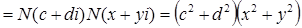
То есть получили, что норма составное число, а по условию есть простое число. Следовательно, наше предположение не верно, и есть простое число.
Ч.Т.Д.
Утверждение.
Если простое натуральное число не является простым гауссовым, то оно представимо в виде суммы двух квадратов.
Доказательство.
Пусть простое натуральное число и не является простым гауссовым. Тогда 
. Так как равны числа, то равны и их нормы. То есть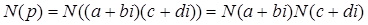 
, отсюда получаем 
.
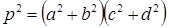Возможно два случая:
1). 
, то есть представили в виде суммы двух квадратов.
2). 
, то есть 
, значит 
обратимое число, чего не может быть, значит этот случай нас не удовлетворяет.
Ч.Т.Д.
|
|
|
