 |
Обратимые и союзные элементы.
|
|
|
|
Посмотрим, какие гауссовы числа будут обратимыми. Нейтральным по умножению является  . Если гауссово число
. Если гауссово число  обратимо, то, по определению, существует
обратимо, то, по определению, существует  такое, что
такое, что 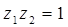 . Переходя к нормам, согласно свойству 3, получим
. Переходя к нормам, согласно свойству 3, получим  . Но эти нормы натуральны, следовательно
. Но эти нормы натуральны, следовательно  . Значит, по свойству 4,
. Значит, по свойству 4,  . Обратно, все элементы данного множества обратимы, поскольку
. Обратно, все элементы данного множества обратимы, поскольку 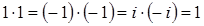 . Следовательно, обратимыми будут числа с нормой равной единице, то есть
. Следовательно, обратимыми будут числа с нормой равной единице, то есть  ,
,  .
.
Как видно не все гауссовы числа будут обратимы. Поэтому интересно рассмотреть вопрос делимости. Как обычно, мы говорим, что 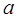 делится на
делится на 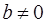 , если существует
, если существует  такое, что
такое, что  .Для любых гауссовых чисел
.Для любых гауссовых чисел  , а также обратимых
, а также обратимых  справедливы свойства.
справедливы свойства.
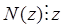 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
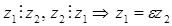 , где
, где  (11)
(11)
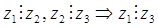 (12)
(12)
Легко проверяются (8), (9), (11), (12). Справедливость (7) следует из (2), а (10) следует из (6). В силу свойства (9), элементы множества 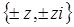 ведут себя по отношению к делимости точно так же как и
ведут себя по отношению к делимости точно так же как и  , и называются союзными с
, и называются союзными с  . Поэтому естественно рассматривать делимость гауссовых чисел с точностью до союзности. Геометрически на комплексной плоскости союзные числа будут отличаться друг от друга поворотом на угол кратный
. Поэтому естественно рассматривать делимость гауссовых чисел с точностью до союзности. Геометрически на комплексной плоскости союзные числа будут отличаться друг от друга поворотом на угол кратный  .
.
ДЕЛЕНИЕ С ОСТАТКОМ.
Пусть надо поделить  на
на  , но невозможно произвести деление нацело. Мы должны получить
, но невозможно произвести деление нацело. Мы должны получить  , и при этом
, и при этом  должно быть «мало». Тогда покажем, чту брать в качестве неполного частного при делении с остатком во множестве гауссовых чисел.
должно быть «мало». Тогда покажем, чту брать в качестве неполного частного при делении с остатком во множестве гауссовых чисел.
|
|
|
Лемма 1. О делении с остатком.
В кольце  возможно деление с остатком, при котором остаток меньше делителя по норме. Точнее, для любых
возможно деление с остатком, при котором остаток меньше делителя по норме. Точнее, для любых  и
и  найдется
найдется  такое, что
такое, что  . В качестве
. В качестве  можно взять ближайшее к комплексному числу
можно взять ближайшее к комплексному числу  гауссово число.
гауссово число.
Доказательство.
Разделим  на
на  во множестве комплексных чисел. Это возможно, так как множество комплексных чисел является полем. Пусть
во множестве комплексных чисел. Это возможно, так как множество комплексных чисел является полем. Пусть  . Округлим действительные числа
. Округлим действительные числа 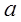 и
и  до целых, получим соответственно
до целых, получим соответственно  и
и  . Положим
. Положим  . Тогда
. Тогда
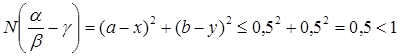 .
.
Умножая сейчас обе части неравенства на  получим, в силу мультипликативности нормы комплексных чисел, что
получим, в силу мультипликативности нормы комплексных чисел, что  . Таким образом, в качестве неполного частного можно взять гауссово число
. Таким образом, в качестве неполного частного можно взять гауссово число 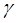 , которое как нетрудно видеть, является ближайшим к
, которое как нетрудно видеть, является ближайшим к 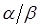 .
.
Ч.Т.Д.
НОД. АЛГОРИТМ ЕВКЛИДА.
Мы пользуемся обычным для колец определением наибольшего общего делителя. НОД’ом двух гауссовых чисел 
 называется такой их общий делитель, который делится на любой другой их общий делитель.
называется такой их общий делитель, который делится на любой другой их общий делитель.
Как и во множестве целых чисел, во множестве гауссовых чисел для нахождения НОД пользуются алгоритмом Евклида.
Пусть  и
и  данные гауссовы числа, причем
данные гауссовы числа, причем  . Разделим с остатком
. Разделим с остатком  на
на  . Если остаток будет отличен от 0, то разделим
. Если остаток будет отличен от 0, то разделим  на этот остаток, и будем продолжать последовательное деление остатков до тех пор, пока оно будет возможно. Получим цепочку равенств:
на этот остаток, и будем продолжать последовательное деление остатков до тех пор, пока оно будет возможно. Получим цепочку равенств:
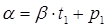 , где
, где 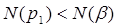
 , где
, где 
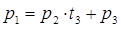 , где
, где 
……………………….
 , где
, где 
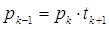
Эта цепочка не может продолжаться бесконечно, так как имеем убывающую последовательность норм, а нормы — неотрицательные целые числа.
Теорема 2. О существовании НОД.
В алгоритме Евклида, примененному к числам Гаусса  и
и  последний ненулевой остаток есть НОД(
последний ненулевой остаток есть НОД( ).
).
Доказательство.
Докажем, что в алгоритме Евклида действительно получаем НОД.
|
|
|
1.Рассмотрим равенства снизу вверх.
Из последнего равенства видно, что  .Следовательно,
.Следовательно,  как сумма чисел делящихся на
как сумма чисел делящихся на  . Так как
. Так как  и
и  , то следующая строчка даст
, то следующая строчка даст  . И так далее. Таким образом, видно, что
. И так далее. Таким образом, видно, что  и
и  . То есть
. То есть  это общий делитель чисел
это общий делитель чисел  и
и  .
.
Покажем, что это наибольший общий делитель, то есть  делится на любой другой их общий делитель.
делится на любой другой их общий делитель.
2. Рассмотрим равенства сверху вниз.
Пусть  — произвольный общий делитель чисел
— произвольный общий делитель чисел 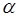 и
и  . Тогда
. Тогда  , как разность чисел делящихся на
, как разность чисел делящихся на  , действительно из первого равенства
, действительно из первого равенства  . Из второго равенства получим, что
. Из второго равенства получим, что  . Таким образом, представляя в каждом равенстве остаток как разность чисел делящихся на
. Таким образом, представляя в каждом равенстве остаток как разность чисел делящихся на  , мы из предпоследнего равенства получим, что
, мы из предпоследнего равенства получим, что  делится на
делится на  .
.
Ч.Т.Д.

|
|
|


