 |
Реакторы с неидеальной структурой потока
|
|
|
|
Цель работы
6.1.1 Обработка экспериментальных данных с трассером при изучении структуры потока в реальном аппарате.
6.1.2 Моделирование реального реактора с помощью неидеальной модели.
6.1.3 Определение параметра модели на основании опытных данных.
Краткие теоретические сведения
В реальных аппаратах структура потока носит более сложный характер, чем в аппаратах с идеальной гидродинамической структурой. Причинами отклонения от идеальности являются такие факторы, как наличие застойных зон, внутренних байпасов и рециклов, молекулярной и турбулентной диффузии, неравномерность поля скоростей и другие факторы.
Экспериментальное определение степени отклонения от идеального гидродинамического режима, а также определение параметров модели может быть проведено на базе изучения функций распределения времени пребывания (интегральной и дифференциальной). Вид функции раскрывает определенным образом структуру потоков взаимодействующих веществ, их перемешивание в реакторе. Он зависит от типа реактора и определяется в значительной степени его конструкцией. Для расчета реактора недостаточно знания истинного времени реакции, полученного из ее кинетического уравнения. Для нахождения степени превращения требуется определение распределения времени пребывания реагирующих веществ в реакционном объеме и условий их перемешивания в нем.
Экспериментально кривые отклика получают путем введения инертного компонента (индикатора или трассера) на входе в реактор по какому-либо способу и регистрации его концентрации на выходе из реактора. Время пребывания индикатора в реакторе такое же, как и частиц основного потока. Интегральная функция распределения F(
) соответствует кривой отклика на ступенчатый сигнал, дифференциальная Е() – на импульсный сигнал.
|
|
|
Связь между средним временем пребывания и дифференциальной функцией распределения имеет вид:
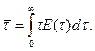(6.1)
Если экспериментальные данные приводятся в дискретной форме, то для расчетов среднего времени пребывания используют приближенную форму уравнения (6.1):
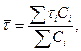(6.2)
где Ci – экспериментальные значения концентрации индикатора.
Дифференциальная функция распределения может быть рассчитана также по приближенной формуле:
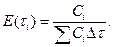(6.3)
Средняя концентрация компонента А на выходе из реактора непрерывного действия с учетом функции распределения имеет вид:
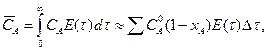(6.4)
где СА – текущая концентрация компонента А, определяемая из кинетического уравнения реакции;
СА0 – начальная концентрация.
Тогда выход по продукту S определится уравнением:
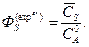(6.5)
Задание
Последовательная реакция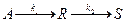 
проводится в реальном реакторе без изменения плотности реакционной смеси. Опыты с трассером при объемной скорости, равной скорости подачи реакционной смеси, приведены на рисунке 6.1.
6.3.1 Используя программу к лабораторной работе № 6 (Приложение А), рассчитать выход по продукту S на основании опытов с трассером. Известно, что для последовательной реакции характеристическое уравнение имеет вид:
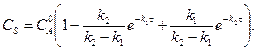(6.6)
6.3.2 Построить модель реактора (записать уравнения материального баланса). В качестве модели принять реактор идеального смешения с байпасом.
Показать, что для реактора смешения концентрация по продукту S может быть определена из уравнения:
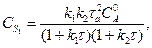(6.7)
где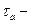 
время пребывания в реакторе идеального смешения.
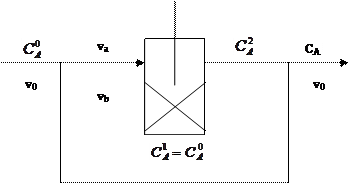
Рисунок 6.1 – Схема модели
Учитывая долю байпаса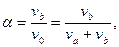 
находим концентрацию продукта S для модели:
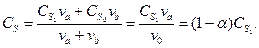(6.8)
Выход по продукту S определяется по уравнению:
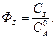(6.9)
6.3.3 Выполнить расчеты на модели с исходными данными, приведенными ниже, с различными значениями параметра модели в заданном интервале. Сравнить расчетное значение выхода продукта S с полученным для реального аппарата. С каким значением параметра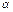 
модель лучше всего описывает реальный реактор? Сделать выводы по работе.
|
|
|
Исходные данные:
k1 =0,01 c-1; k2=0,007 c-1 – константы скорости реакции;
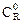= 0;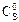 
= 0 – начальные концентрации компонентов R и S соответственно.
Экспериментальные значения времени пребывания и концентрации трассера приведены в таблице 6.1 по вариантам.
Таблица 6.1 – Варианты заданий
| Номер варианта Номер опыта | ||||||||||
| ·0,1
| С | ·0,1
| С |
| С |
| С |
| С | |
| 15,4 | 4,6 | |||||||||
| 16,2 | 4,5 | |||||||||
| 16,0 | 4,2 | |||||||||
| 14,8 | 3,8 | |||||||||
| 10,2 | 2,7 | |||||||||
| 7,9 | 1,8 | |||||||||
| 6,3 | 1,1 | |||||||||
| 5,2 | 0,7 | |||||||||
| 4,3 | 0,4 | |||||||||
| 3,6 | 0,2 | |||||||||
| 3,0 | 0,1 | 11,5 | ||||||||
| 2,5 | 0,0 | |||||||||
| 2,0 | 8,5 | |||||||||
| 1,8 | ||||||||||
| 1,5 | ||||||||||
| 1,2 | ||||||||||
| 0,8 | ||||||||||
| 0,6 | 3,5 | |||||||||
| 0,4 | ||||||||||
| 0,3 | 2,5 | |||||||||
| 0,2 | ||||||||||
| 0,1 | 1,5 | |||||||||
| 0,1 | ||||||||||
| 0,1 | 0,5 | |||||||||
| 0,0 | 0,0 |
Продолжение таблицы 6.1
| Номер варианта Номер опыта | |||||||||||
| ·0,1
| С | ·0,1
| С |
| С |
| С |
| С | ||
| 25,3 | 8,4 | 36,8 | |||||||||
| 24,2 | 8,0 | 31,9 | |||||||||
| 22,0 | 7,2 | 27,6 | |||||||||
| 20,8 | 6,8 | 21,8 | |||||||||
| 16,2 | 6,3 | 18,5 | |||||||||
| 12,9 | 5,8 | 15,0 | |||||||||
| 11,3 | 5,1 | 12,4 | |||||||||
| 9,2 | 4,7 | 10,6 | |||||||||
| 8,3 | 4,4 | 0,9 | |||||||||
| 7,6 | 3,2 | 0,8 | |||||||||
| 6,0 | 2,7 | 0,6 | |||||||||
| 5,5 | 2,3 | 0,5 | |||||||||
| 4,1 | 2,0 | 0,3 | |||||||||
| 3,8 | 1,5 | 0,2 | 8,5 | ||||||||
| 3,5 | 1,1 | 0,1 | 7,3 | ||||||||
| 3.2 | 0,8 | 0,1 | 6,2 | ||||||||
| 2,8 | 0,5 | 0,0 | 5,1 | ||||||||
| 1,6 | 0,3 | 4,2 | |||||||||
| 1,4 | 0,1 | 3,6 | |||||||||
| 0,9 | 0,0 | 2,9 | |||||||||
| 0,8 | 2,0 | ||||||||||
| 0,6 | 1,1 | ||||||||||
| 0,5 | 0,8 | ||||||||||
| 0,3 | 0,5 | ||||||||||
| 0,1 | 0,1 | ||||||||||
|
|
|
6.4 Контрольные вопросы
1. Каким образом экспериментально изучают структуру потока в реакторах?
2. Какие требования предъявляются к трассеру?
3. Каковы причины отклонения структуры потока в реакторах от идеальной?
4. Основные допущения о движении потока в реакторе идеального смешения.
5. Какое значение имеет структура потока в реакторе при проведении химической реакции?
Лабораторная работа № 7.
|
|
|
