Отдельные пузырьки воздуха

Размер единичных пузырьков, выходящих из отверстий при низкой скорости, определяется из уравнения:

, (1.1)

где – диаметр пузырька, м;

– диаметр отверстия трубки барботера, м;

– разность плотности между жидкостью и газом (воздухом), кг/м³;

– поверхностное натяжение жидкости, Н/м.

Левая часть уравнения (1.1) выражает подъемную силу пузырька, а правая часть уравнения выражает силу, удерживающую пузырек
в отверстии. Уравнение практически верно для изменения производительности по газу 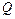в пределах от 0,02 до 0,5 см³/с.

Рассмотренные условия соответствуют пузырьковому режиму работы барботера, когда в жидкости всплывают отдельные пузыри, диаметр которых определяется диаметром отверстий барботера, свойствами жидкости и не зависит от давления (при изменении его до 10⁶ Па).

Размер одиночных газовых пузырей, отрывающихся от отверстия диаметром = от 1 до 5 мм, можно определить на основе уравнения баланса сил (1.1):

, (1.2)

где .

Таким образом, величина пропорциональна корню кубическому из диаметра отверстия 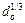и не зависит от величины потока газа 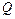. Однако это отношение не соблюдается, когда значение диаметра превышает указанный выше предел.

При аэрации в промышленных ферментаторах применяется следующее эмпирическое выражение:

. (1.3)

При ламинарном режиме движения одиночного пузыря, когда 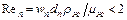, скорость его всплытия может быть рассчитана по упрощенной формуле Адамара-Рыбчинского:

, (1.4)

где – вязкость жидкой среды, .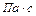

Из этих данных следует, что в воде, например, будут всплывать при ламинарном обтекании воздушные пузырьки, имеющие диаметр мм. Такие пузырьки могут отрываться от отверстий очень малых размеров. Промышленные барботеры имеют диаметр отверстий >0,4 мм, поэтому в большинстве случаев движение свободно всплывающего одиночного пузыря турбулентно, и осредненная скорость его подъема рассчитывается по формуле:

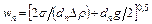. (1.5)

Экспериментальные данные по определению зависимости между диаметром пузырька и конечной скоростью подъема пузырька в воде представлены на рисунке 1.3 [1]. Ван Клевеленом и др. доказано, что значение почти пропорционально величине , когда 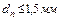. В этой области пузырьки почти сферические по форме. Если значение увеличивается от 1,5 до 6 мм, то форма пузырьков начинает заметно изменяться. Пузырьки принимают грибовидную форму, когда значение превышает 6 мм.

В промышленных ферментаторах пузырьки воздуха имеют диаметр от 1,5 до 10 мм. Скорость подъема пузырька может колебаться от 20 до 30 см/с для случая единичных пузырьков в разбавленной культуральной среде, характеристики которой близки к воде (см. рису-
нок 1.3).

 

Поток пузырьков воздуха

Практически в промышленных процессах единичные пузырьки встречаются редко. В большинстве случаев приходится иметь дело
с потоком пузырьков. Если не наблюдается коалесценции пузырьков
в процессе аэрации, а также заметного разнообразия в диаметрах пузырьков, то величина для единичных пузырьков может быть применена и для потока пузырьков воздуха. При массовом барботаже
в пузырьковом режиме образуется полидисперсная система пузырей.
В этом случае, поскольку трудно выбрать характерный размер пузыря,

для расчета большинство исследователей рекомендуют пользоваться формулой:

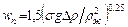. (1.6)

В присутствии механического перемешивания в аппарате на движение пузырьков влияет турбулентность, вызванная мешалками. При ферментации пузырьки деформируются и значительно изменяются в диаметре. При вышеуказанных обстоятельствах определение скорости по рисунку 1.3 для потока пузырьков воздуха становится неприемлемым. Поэтому предложено получать приближенные значения скорости с помощью следующего соотношения:

, (1.7)

где – задержка пузырьков [1];

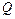– скорость аэрации, м³/с;

– высота столба жидкости, м;

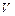– объем жидкости, м³.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: