 |
Методические указания к заданию 3.3
|
|
|
|
Основная идея сокрытия информации с помощью рассматриваемого способа состоит в том, что делают разное число пробелов в конце каждого предложения контейнера. Причём для внедрения 0 делают два пробела, а для внедрения 1 – один пробел. Очевидно, что пропускная способность такой стеганосистемы низкая. С помощью одного предложения открытого текста можно передать лишь один бит. Если принять, что среднее предложение состоит из восьми слов по семь букв, то пропускная способность составит 0,002.
Программа для сокрытия информации в текстовых документах находится в папке Задание_3 (имя файла – Probely_Lab.xmcd). Пустой контейнер сохранен с именем cont.txt. Контейнер с внедрённой информацией имеет имя m_per.txt. Принятое сообщение хранится в текстовом документе с именем m_prm.txt.
По заданию требуется скрыть в контейнере одну букву (то есть 8 бит информации). Это означает, что пустой контейнер должен содержать не менее восьми предложений. Признаком предложения является сочетание двух символом: точки и пробела.
Таким образом, для выполнения задания необходимо создать текстовый документ, в который нужно вписать заданную немецкую пословицу. Очевидно, что пословица не позволит скрытно передать 8 бит информации. Поэтому текст пословицы должен быть дополнен несколькими предложениями.
Рассмотрим, как это можно сделать.
Пример.
Пусть задан текст, в котором нужно скрытно передать 1 байт информации:
Er ist das fünfte Rad am Wagen.
Дополним его символами, среди которых чаще всего встречаются точки и пробелы (они имитируют предложения).
Er ist das fünfte Rad am Wagen. 1. 2. 3. 4. 5. 6. 7. 8.
Такой (или подобный) контейнер можно использовать для скрытой передачи информации.
Указанные дополнения пословиц цифрами сделаны для уменьшения объёма набираемого текста и для большей концентрации на идее сокрытия информации.
|
|
|
Далее приведён текст программы.












Требования к отчёту
Отчёт подготавливается в электронном виде. Он должен содержать рисунок, в который внедрён указанный в задании текст, десятичные значения цветовых составляющих указанных пикселей, текстовый документ с внедрённым символом, листинги использованных программ.
6. Контрольные вопросы
6.1. Какие математические системы Вы знаете?
6.2. Что означает аббревиатура LSB?
6.3. Как с помощью матрицы цветовых составляющих определить значения компонент R, G, B для заданного пикселя?
6.4. Как по известному размеру графического контейнера формата BMP определить максимальный объем внедряемого сообщения методом LSB?
6.5. Перечислите методы внедрения информации в текстовые документы.
6.6. Перечислите форматы графических файлов.
6.7. Перечислите цветовые модели.
Список литературы
1. Конахович Г.Ф., Пузыренко А.Ю. Компьютерная стеганография. Теория и практика. К.: МК-Пресс, 2006. — 288 с. — ISBN: 966-8806-06-9
Лабораторная работа 29
Решение математических задач с помощью Mathcad
Цель работы
Получить навыки выполнения простейших вычислений и составления программ в PTC Mathcad Prime 3.0, изучить три классических симметричных шифра и асимметричный шифр RSA.
Общие сведения
Отличительной особенностью математической системы Mathcad является одновременное присутствие в документах текста, самой программы и продуктов её работы (в виде формул, программ, результатов расчёта, таблиц, графиков и итогов символьного преобразования аналитических формул). Вид документа напоминает научную статью.

Основные команды размещены на ленте, которая может быть настроена по усмотрению конкретного пользователя.
|
|
|
Вид уравнений в основном совпадает с привычной математической записью. Писать формулы можно по всей свободной площади листа. Математическая система подбирает размеры для дробей, скобок и других математических символов так, чтобы они были пропорциональными и выглядели в привычном виде.
В системе используются стандартные символы для обозначения суммы, произведения, интеграла, производной, предела и т. д. Однако некоторые особенности синтаксиса системы приводят к частым ошибкам при записи формул.
Например, вместо необходимой для системы записи sin(x)2 часто ошибочно записывают sin2x. В Mathcad принято аргумент указывать в круглых скобках, которые должны располагаться сразу за именем функции.
Первоначально нелогичным кажется использование в системе нескольких знаков определения и вычислений.

Например, в следующем примере использованы три операции присвоения (назначения) переменным некоторых числовых значений, а четвертая операция выводит на экран результат суммирования. В этих случаях используются разные символы.

Существует оператор глобального присвоения, который сохраняет назначенное значение во всём документе. Попытка присвоить глобальной переменной новое значение приведёт к неудаче.
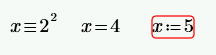
Ещё один символ (стрелка) служит для запуска в действие символьных операций:

Символ сравнения (жирный знак равенства) имеет конфигурацию, сходную с конфигурацией рассмотренных знаков. Однако он используется иначе, например, для нахождения корней квадратного уравнения:

В режиме программирования используется ещё один вид присвоения (стрелка, направленная справа-налево).

Некоторое представление о возможностях математической системы даёт вкладка Функции. Предлагаемый набор функций позволяет успешно решать большинство инженерных задач.

Данная математическая система позволяет выполнять разнообразные математические преобразования, в том числе есть возможность использовать логические функции, изучение которых необходимо в курсе «Информатика». На рисунке показан пример работы с наиболее часто используемыми логическими функциями в векторной форме.
|
|
|

Естественно, что в Mathcad доступна не только Булева алгебра, но и обычная алгебра. Следующий рисунок показывает примеры арифметических операций в матричной форме.

В Mathcad можно задавать точность проводимых вычислений и определять форму чисел, в которой выводится результат.

Математическая система позволяет строить двухмерные и трёхмерные графики. На следующем рисунке показан график, построенный в прямоугольной системе координат.

Расположение мест заполнения вида функции и аргумента первоначально кажется непривычным. Нагляднее располагать обозначение функции вдоль вертикальной оси, а имя аргумента вдоль горизонтальной. Ради справедливости следует отметить, что надписи (легенды) можно перемещать по графику.
На следующих рисунках показан график в полярной системе координат и трёхмерный график.


|
|
|


