 |
Методические указания к заданию 3.6
|
|
|
|
Это задание иллюстрирует принцип криптографической защиты информации.
Пусть на передающей стороне имеется сообщение (Message) в виде матрицы М, содержащей описание (изображение) какой-либо буквы. Для того чтобы скрыть от противника содержание сообщения его нужно зашифровать. В данном задании шифрование производится аддитивным методом (методом гаммирования). Для получения криптограммы С (Crypto) выполняется сложение с помощью логической операции Исключающее ИЛИ сообщения М с псевдослучайной матрицей G (Gamma).
Заметим, что матрица G должна быть известной лишь на передающей и на приёмной сторонах. Для криптоаналитиков она должна быть неизвестной и трудно вычислимой.
Зашифрованное сообщение (матрица С) передаётся по открытому каналу связи на приёмную сторону, где для дешифрования выполняется её сложение с гаммой (G).
Рассмотрим пример выполнения этого задания.
Предположим, что с передающей стороны отправлено сообщение в виде латинской буквы «F», записанной в матрицу 8x8 в виде единиц на фоне нулей. Для защиты от несанкционированного ознакомления с сообщением нужно исказить сообщение М так, чтобы затруднить чтение для третьей стороны (криптоаналитиков). Процесс преднамеренного искажения сообщения на передающей стороне называется шифрованием.

Шифрование в данном случае производится путём поэлементного суммирования сообщения М с псевдослучайной матрицей G, для формирования которой используется фамилия студента. Понятно, что это делается лишь в учебных целях. В реальных случаях для формирования гаммы должен использоваться генератор случайных чисел.
Будем считать, что фамилия студента – Пфердман. При выполнении задания длина фамилии студента может оказаться не равной восьми буквам. В этом случае длинные фамилии нужно использовать частично, а короткие фамилии дополнять буквами имени (и отчества) студента.
|
|
|
Для формирования матрицы G вначале составим таблицу со значениями двоичных чисел.
| Буквы | Десятичный код | Двоичный код |
| П | 207 | 11001111 |
| ф | 244 | 11110100 |
| е | 229 | 11100101 |
| р | 240 | 11110000 |
| д | 228 | 11100100 |
| м | 236 | 11101100 |
| а | 224 | 11100000 |
| н | 237 | 11101101 |
Двоичные числа из третьего столбца таблицы нужно перенести в матрицу G.

После суммирования матриц получим криптограмму:

Криптограмма передаётся по открытому каналу связи. На приёмной стороне выполняется расшифрование криптограммы. Для этого выполняется опять операция Исключающее ИЛИ над матрицами С и G.

Полученная матрица Р точно совпадает с отправленной матрицей М, хотя по каналу связи передавалась «искажённая» матрица С. По виду матрицы C противнику сложно понять какая буква передавалась по каналу связи.
Вид матрицы G известен только на передающей и приёмной сторонах. Сложность дешифрации сообщения третьей стороной состоит в том, что криптоаналитикам неизвестен вид матрицы G. Если сделать попытку подобрать вид матрицы G, то результат будет многозначным. При разных матрицах G можно получить любую букву открытого текста, а это значит, что криптоанализ не достигает необходимого результата.
Рассмотрим пример.
Пусть криптоаналитик сделал предположение, что для формирования криптограммы на передающей стороне была использована матрица G1, показанная на следующем рисунке.

Суммирование матриц С и G1 даст матрицу Р1, вид которой не совпадает с матрицей М.

На полученной матрице видна буква К (вместо F).
Показанный пример демонстрирует бессмысленность подбора криптоаналитиком гаммы, так как может быть получен любой символ (русские, латинские буквы, цифры, математические знаки, иероглифы и т.п.).
|
|
|
Если гамма формируется правильно, то аддитивный метод считается теоретически криптостойким. Неверное формирование гаммы иллюстрирует следующий пример.
Пусть на передающей стороне в качестве гаммы используется матрица G2, содержащая только единицы. В результате «шифрования» с помощью такой гаммы на криптограмме С2 чётко просматривается открытый текст (буква F только в инверсном виде).
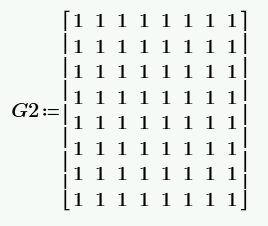

Если матрица гаммы содержит только нули, то в канал связи будет передан открытый текст.
Таким образом, при формировании гаммы одинаково плохо для криптостойкости наличие большого числа единиц и наличие большого числа нулей. Поэтому одним из требований к формированию гаммы является равновероятное появление единиц и нулей.
|
|
|


