Методы контурных токов и узловых потенциалов

УДК 621.3.011

Г94

Отрецензировано на кафедре «Теоретическая и общая электротехника» Нижегородского государственного технического университета им. Р.Е. Алексеева.

 

Гуляев, В.В.

Лабораторные работы по теоретическим основам электротехники: учеб.-метод. пособие для студ. оч. и заоч. обуч. спец-ти 180407 «Эксплуатация судового электрооборудования и средств автоматики» / В.В. Гуляев, А.А. Кралин, А.С. Репин. – Н. Новгород: Изд-во ФГБОУ ВО «ВГУВТ», 2015. – 48 с.

 

 

Учебно-методическое пособие содержит задания и методические указания к лабораторным работам по основным разделам дисциплины «Теоретические основы электротехники». Лабораторные работы связаны с исследованиями цепей постоянного и переменного однофазного и трехфазного тока, переходных процессов в цепях первого и второго порядка, а также в нелинейных цепях.

Работы проводятся на физических установках (стендах). Рекомендуется для студентов очного и заочного обучения.

 

Для студентов очного и заочного обучения.

 

Работа рекомендована к изданию кафедрой электротехники и электрооборудования объектов водного транспорта (протокол № 10 от 10.06.2014 г.).

 

 

© ФГБОУ ВО «ВГУВТ», 2015

Лабораторная работа № 1

Изучение методов расчета линейных

Электрических цепей

Цель работы: опытное подтверждение специальных методов расчета в сложных электрических цепях.

Метод наложения токов

В любой линейной электрической цепи ток или напряжение в любой ветви всегда можно определить как алгебраическую сумму частичных токов или напряжений, вызванных действием источников ЭДС или тока каждого в отдельности (рис. 1.1).

 

Рис. 1.1

 

В соответствии с принципом суперпозиции схему (см. рис. 1.1) можно представить с помощью двух схем (рис. 1.2; 1.3).

 

Рис. 1.2	Рис. 1.3

 

 

– частичные токи.

Токи в ветвях исходной схемы определяются алгебраической суммой частных токов этой ветви:

 

(1.1)

 

Каждая схема (рис. 1.2 и 1.3) рассчитывается отдельно, например, методом эквивалентных сопротивлений.

Для схемы (рис. 1.2):

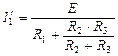;	(1.2)
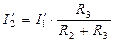;	(1.3)
.	(1.4)

Программа работы

 

1. Собрать схему рис. 1.1 с параметрами Е₁, Е₂, R₁, R₂, R₃ по заданию преподавателя и измерить переносным вольтметром В7–40 напряжения на всех элементах схемы: U_R1, U_R2, U_R3. Результаты занести в табл. 1.1.

Таблица 1.1

№	ИЗМЕРЕННЫЕ ВЕЛИЧИНЫ	ВЫЧИСЛЕННЫЕ ВЕЛИЧИНЫ
п/п	UR1, B	UR2, B	UR3, B	I1, A	I2, A	I3, A

 

2. Закоротив источник Е₂, получить схему рис. 1.2. Измерить напряжения на элементах схемы U_R1, U_R2, U_R3. Результаты занести в табл. 1.1.

3. Закоротить источник Е₁. В полученной схеме рис. 1.3 измерить напряжения U_R1, U_R2, U_R3; результаты занести в табл. 1.1.

4. По заданным величинам R₁, R₂, R₃ определить токи в ветвях схем рис. 1.1, 1.2, 1.3. Результаты занести в табл. 1.1.

5. По исходным данным рассчитать теоретически схему рис. 1.1 методом наложения и полученный результат сравнить с экспериментом.

Содержание отчета:

– схемы рис. 1.1–1.3;

– табл. 1.1;

– вычисления согласно п.п. 4 и 5 программы работы;

– выводы.

Варианты заданий

Таблица 1.2

№ варианта	Е1, В	Е2, В	R1, Ом	R2, Ом	R3, Ом

 

Метод эквивалентного генератора

Согласно теореме об активном двухполюснике, схемы рис. 1.4, а и 1.4, б эквивалентны. Ток в ветви АВ можно определить, используя закон Ома:

.

(1.5)

 

а	б
Рис. 1.4

 

Неизвестные величины Е_э и R_э можно определить, проделав опыты холостого хода (хх) и короткого замыкания (кз) со схемой рис. 1.4, а:

;	(1.6)
.	(1.7)

 

Кроме того, ток в выделенной ветви можно рассчитать теоретически (без проведения эксперимента), используя метод эквивалентного генератора. Последовательность расчета при этом такова:

1. Рассчитать любым методом напряжение на зажимах разомкнутой ветви U_АВХХ.

2. Определить входное сопротивление R_ВХ всей цепи по отношению к зажимам АВ при закороченных источниках ЭДС и разомкнутых ветвях, содержащих источники тока.

Подсчитать искомый ток по формуле:

.

(1.8)

 

Программа работы

1. Собрать схему двухполюсника рис. 1.5 со следующими параметрами: Е₁, R₁, R₂, R₃, R₄ (по заданию преподавателя).

2. Подключить к зажимам двухполюсника исследуемую ветвь (рис. 1.5, а) и измерить ток в ветви с сопротивлением R (по заданию преподавателя), результат занести в табл. 1.3.

3. Подключить к зажимам двухполюсника АВ вольтметр (рис. 1.5, б) и записать измеренное значение напряжения хх (U_АВХХ) в табл. 1.3.

 

	а	б	в
Рис. 1.5

 

4. Подключить к зажимам АВ амперметр и измерить ток кз (I_АВКЗ), занеся результат в табл. 1.3.

5. По результатам опытов хх и кз определить внутреннее сопротивление двухполюсника R_Э (см. (1.7)) и вычислить силу тока в диагонали мостовой схемы (ветвь с сопротивлением R) по формуле (1.5). Результаты вычисления сравнить с экспериментом (п. 2).

6. Используя известные значения сопротивлений R₁, R₂, R₃, R₄, R и напряжения источника питания Е₁, рассчитать методом эквивалентного генератора силу тока в ветви с сопротивлением R. Результаты измерений и вычислений занести в табл. 1.3.

Таблица 1.3

ИЗМЕРЕННЫЕ ВЕЛИЧИНЫ	ВЫЧИСЛЕННЫЕ ВЕЛИЧИНЫ
U АВХХ, В	IАВКЗ, А	IR, А	по результатам опытов (п. 5)	теоретически (п. 6)
RЭ, Ом	IR, A	IR, A

Содержание отчета:

– рис. 1.5;

– табл. 1.3;

– вычисления согласно п.п. 5, 6 программы работы;

– выводы.

Варианты заданий

Таблица. 1.4

№ варианта	Е1, В	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R, Ом
						12,5
						8,3
	7,5					8,3

Методы контурных токов и узловых потенциалов

Сложная электрическая цепь (например, такая как на рис. 1.6) может быть рассчитана по законам Кирхгофа, а также методами контурных токов и узловых потенциалов. Подробно алгоритм составления уравнений данными методами приведен в [5].

Программа работы

1. В соответствии с индивидуальным вариантом нарисовать развернутую электрическую схему с шестью ветвями (например, как на рис. 1.6).

2. Найти токи в заданной схеме по законам Кирхгофа.

3. Найти токи в заданной схеме методом контурных токов.

4. Найти токи в заданной схеме методом узловых потенциалов.

5. Составить уравнение баланса мощностей рассматриваемой цепи.

Рис. 1.6

Таблица 1.5

Конфигурация и состав элементов электрической цепи

 

Вариант индивидуальный	№ схемы рис. 1.7	Номера ветвей
		RE	R	RE	R	RE	R
		R	RE	R	RE	R	RE
		RE	R	RE	RE	R	R
		R	RE	RE	R	R	RE
		RE	RE	R	RE	R	R
		RE	R	RE	R	RE	R
		R	RE	RE	R	RE	R
		R	R	RE	RE	RE	R
		RE	R	RE	R	R	RE
		R	RE	RE	RE	R	R
		R	R	R	R	R	R
		RE	R	RE	R	R	RE
		R	R	R	RE	RE	RE
		R	RE	RE	R	RE	R
		RE	R	RE	R	R	RE
		RE	R	RE	RE	R	R
		R	RE	R	RE	RE	R
		RE	R	RE	R	R	RE
		R	RE	R	RE	RE	R
		RE	R	RE	RE	R	R
		R	RE	RE	R	R	RE
		R	RE	R	RE	RE	R
		RE	R	RE	R	R	RE
		R	RE	RE	RE	R	R
		RE	R	R	RE	RE	R
		R	RE	RE	R	R	RE
		R	R	RE	RE	RE	R
		RE	R	RE	R	R	RE
		RE	R	R	RE	RE	R
		R	RE	RE	R	R	RE

Таблица 1.6

12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: