Значения параметров источников и резисторов электрической цепи

 

Групповой вариант
Е1
Е2
Е3
Е4
Е5
Е6
R1
R2
R3
R4
R5
R6

 

Рис. 1.7. Графы электрических схем

Содержание отчета:

– схема, соответствующая варианту, с указанными на ней токами, контурными токами, обозначениями узлов;

– вычисления согласно п.п. 2–5 программы работы;

– выводы.

Контрольные вопросы и задания

1. В чем заключается принцип наложения токов?

2. Может ли ЭДС источника быть направленной против тока?

3. Почему метод наложения нельзя использовать для расчета нелинейных электрических цепей и расчета мощностей?

4. Что называется активным и пассивным двухполюсником?

5. Для каких случаев расчета электрических цепей применяется метод эквивалентного генератора? Почему для этих случаев удобно применять указанный метод?

6. Как производятся опыты хх и кз?

7. Что такое внутреннее сопротивление двухполюсника?

8. Объяснить алгоритм составления уравнений по законам Кирхгофа.

9. Пояснить идею метода контурных токов.

10. Пояснить идею метода контурных токов.

11. Что такое баланс мощностей?

12. Дать общую характеристику методов расчета сложных электрических цепей.

 

 

Лабораторная работа № 2

Исследование процессов в однофазных цепях

Синусоидального тока

Цель работы: исследование электрических цепей синусоидального тока с последовательным, параллельным и смешанным соединением элементов.

Общие сведения

Энергетические процессы в цепях синусоидального тока характеризуется активной Р, реактивной Q, полной S и комплексной мощностями.

Активная мощность Р соответствует электроэнергии, которая необратимо преобразуется в другой вид энергии в активном приемнике и определяется соотношением:

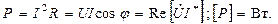
(2.1)

Реактивная мощность Q характеризует энергию, которой обмениваются генератор и приемник:

(2.2)

Полная мощность S соответствует той мощности, которую источник может отдавать потребителю, если последний будет работать при cos j = 1:

.

(2.3)

Активная мощность Р является действительной, а реактивная мощность Q – мнимой частью полной комплексной мощности:

(2.4)

В цепи (рис. 2.1, а), содержащей активное сопротивление R_L и индуктивность L, вектор активного напряжения U_R совпадает с вектором тока, вектор индуктивного напряжения U_L опережает ток на угол 90° (рис. 2.1, б).

 

	а	б	в	г
Рис. 2.1

 

а	б	в	г
Рис. 2.2

На основе векторной диаграммы (рис. 2.1, б) можно построить треугольники сопротивлений (рис. 2.1, в) и мощностей (рис. 2.1, г). Все эти треугольники подобны, причем в противоположность векторной диаграмме треугольники мощностей и сопротивлений состоят из отрезков, а не векторов, так как сопротивления и мощности – скалярные величины.

Полное сопротивление цепи:

,

(2.5)

где – активное сопротивление, а – индуктивное сопротивление.

Полная мощность цепи:

,

(2.6)

где – активная мощность; – индуктивная мощность.

В неразветвленной цепи, содержащей активное сопротивление R_C и емкость С (рис. 2.2, а), вектор активного напряжения U_R совпадает с вектором тока, а вектор емкостного напряжения U_С отстает от тока на угол 90° (рис. 2.2, б). Треугольники сопротивлений и мощностей для такой цепи приведены на рис. 2.2, в, г. Полное сопротивление цепи, а также мощность определяются аналогично соотношениям, приведенным для предыдущей схемы с последовательным соединением R_L и L.

 

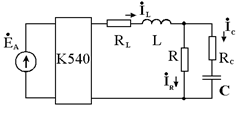Рис. 2.3

В случае смешанного соединения элементов (рис. 2.3) применяется символический метод расчета цепей синусоидального тока. При этом последовательность расчета такая же, как для цепи постоянного тока.

По результатам расчета строится векторная диаграмма цепи.

В схеме должен соблюдаться баланс мощностей:

 

,

(2.7)

 

где		–	сумма мощностей источников ЭДС;
	–	сумма мощностей источников тока;
	–	сумма мощностей активных элементов цепи;
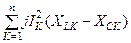
	–	сумма мощностей реактивных элементов цепи.

 

Программа работы

1. Собрать схему рис. 2.1, а, замерить величины I, U, P, результаты занести в табл. 2.1.

2. Собрать схему рис. 2.2, а, измерить комплектом K540 I, U, P в цепи, полученные результаты записать в табл. 2.1.

3. Собрать схему рис. 2.3; замерив значения I, U, P по комплекту K540, занести результаты в табл. 2.1.

4. Используя результаты эксперимента (п.п. 1 и 2), рассчитать параметры схем замещения катушки R_L и L и конденсатора R_C и C. Результаты занести в табл. 2.1.

5. Построить в масштабе векторные диаграммы для схем рис. 2.1, а и рис. 2.2, а, треугольники сопротивлений (схема рис. 3.1, а), проводимостей (схема рис. 2.2, а), мощностей (рис. 2.1, а и 2.2, а).

6. По известным параметрам R_L, L, R_C, C, R рассчитать все токи, напряжения на всех элементах и всех ветвях в схеме рис. 2.3.

По результатам расчета построить векторную диаграмму. Определить мощности P, Q, S всех ветвей и всей цепи. Составить баланс мощностей. Сравнить результаты расчета с экспериментом (P, I, определенные с помощью K540).

 

Таблица 2.1

 

Эксперимент	Расчет
U, B	I, A	P, Вт	RL(C ),Ом	S, BА	Z, Ом	Q, BAp	XL, Ом	L, Гн	j,º	XC, Ом	C, Ф
										–	–
							–	–
			–	–	–	–	–	–	–	–	–

 

Расчетные формулы

;	(2.1’)
;	(2.5’)
;	(2.6’)
;	(2.8)
;	(2.9)
.	(2.10)

Содержание отчета:

– схемы рис. 2.1, а, 2.2, а, 2.3;

– табл. 2.1;

– расчеты и графические построения согласно п.п. 4, 5, 6;

– выводы.

Варианты заданий

Таблица 2.2

№ варианта	Катушка индуктивности	Резистор	Конденсатор
	L1	R = 10 Ом	С = 40 мкФ
	L1	R = 50 Ом	С = 50 мкФ
	L1	R = 30 Ом	С = 70 мкФ
	L1	R = 10 Ом	С = 90 мкФ
	L1	R = 50 Ом	С = 120 мкФ
	L1	R = 10 Ом	С = 150 мкФ

 

Контрольные вопросы

1. Чему равно индуктивное сопротивление, и в каких единицах оно измеряется? Емкостное сопротивление?

2. Каким образом можно изменить индуктивное сопротивление? Емкостное сопротивление? Их физическая сущность?

3. Что такое активная и реактивная мощности однофазной цепи переменного тока и в каких единицах их измеряют?

4. Чему равна полная мощность однофазной цепи переменного тока и в каких единицах ее измеряют?

5. Что такое коэффициент мощности?

6. Как рассчитать проводимость для параллельного соединения резистора и идеального конденсатора?

7. Как строятся треугольники токов, проводимостей, мощностей для разветвленной цепи с активно-емкостной нагрузкой?

8. Как строятся треугольники напряжений, сопротивлений, мощностей для цепи с последовательно соединенными R и L?

9. Что произойдет, если катушку индуктивности, рассчитанную для работы в цепях переменного тока, включить в цепь постоянного тока с таким же значением напряжения?

10. Как строится векторная диаграмма цепи синусоидального тока со смешанным соединением элементов?

 

 

Лабораторная работа № 3

Резонанс напряжений

Цель работы: исследовать частотные свойства электрических цепей и основные особенности режима резонанса при последовательном соединении индуктивной катушки и конденсатора.

Общие сведения

В электрических цепях переменного тока, содержащих индуктивные и емкостные элементы, может возникать особый режим работы, называемый режимом резонанса. Этот режим характеризуется тем, что входное сопротивление цепи является чисто активным, и, следовательно, входные ток и напряжения совпадают по фазе.

При последовательном соединении катушки индуктивности и конденсатора (рис. 3.1), когда их реактивные сопротивления X_L и X_C становятся равными друг другу, возникает резонанс напряжений.

Рис. 3.1

Равенство реактивных сопротивлений X_L и X_C (ωL = 1/ωC) может быть получено изменением емкости, индуктивности или частоты питающей сети. В данной работе явление резонанса достигается путем изменения частоты до резонансного значения w_p:

.

(3.1)

Действующее значение тока в исследуемой цепи (см. рис. 3.1) определяется выражением:

,

(3.2)

 

где	U	–	напряжение на входе схемы;
R = RL + RC	–	активное сопротивление цепи.

 

Как видно из выражения (3.2), при резонансе ток в цепи достигает максимального значения, поскольку в этом случае полное сопротивление цепи минимально: = R.

Зависимости от частоты w (или f) действующих значений напряжений U_L и U_C, сопротивлений X_L, X_C и X, действующего значения тока I, угла j и других электрических величин и параметров, относящихся к данной цепи, называются ее частотными характеристиками. Их примерный вид показан на рис. 3.2.

Программа работы

1. Собрать схему рис. 3.1.

2. Изменяя частоту источника питания (10–12 значений, включая f_р), исследовать режимы работы цепи. Результаты измерений занести в табл. 3.1.

Рис. 3.2

 

3. Используя данные измерений, рассчитать указанные в табл. 3.1 величины:

– активное сопротивление цепи

;

(3.3)

– индуктивное сопротивление катушки

;

(3.4)

– емкостное сопротивление конденсатора

;

(3.5)

– реактивное сопротивление цепи

;

(3.6)

– индуктивное напряжение

;

(3.7)

– емкостное напряжение

;

(3.8)

– величину угла j

.

(3.9)

Примечание. Параметры схем замещения катушки индуктивности (R_L и L) и конденсатора (R_C и С) рассчитаны в лабораторной работе № 2.

4. По данным табл. 3.1 построить частотные характеристики цепи рис 3.1.

5. Определить расчетным путем резонансную частоту w_р и сравнить результат с экспериментом.

6. Построить в масштабе векторные диаграммы исследуемой цепи для трех различных режимов:

– X_L < X_C;

– X_L = X_C;

– X_L > X_C.

Таблица 3.1

№ опыта

Эксперимент

Расчет

f, Гц

U, B

I, A

P, Вт

R, Ом

XL, Ом

XC, Ом

Х, Ом

UL,B

UC, B

j,º

 

Содержание отчета:

– схема исследуемой цепи (см. рис. 3.1);

– табл. 3.1;

– расчет и графические построения согласно п.п. 3, 4, 5, 6 программы работы;

– выводы.

Варианты заданий

Таблица 3.2

№ варианта	Катушка индуктивности	Конденсатор
	L1	С = 40 мкФ
	L1	С = 50 мкФ
	L1	С = 70 мкФ
	L1	С = 90 мкФ
	L1	С = 120 мкФ
	L1	С = 150 мкФ

Контрольные вопросы и задания

1. Объясните, при каких условиях и в какой цепи возникает резонанс напряжений. Каковы признаки возникновения резонанса напряжений?

2. В чем могут заключаться эксплуатационные опасности, связанные с явлением резонанса в реальных условиях и цепях?

3. Опишите энергетический процесс в цепи (см. рис. 3.1) при резонансе напряжений.

4. При каких условиях в цепи, содержащей катушку и конденсатор, мог бы иметь место незатухающий колебательный процесс?

 

Лабораторная работа № 4

Исследование процессов

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: